中考模拟考试卷《数学》
(考试时间120分钟 满分150分)
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
一.选择题(每小题4分,共48分,每题中只有一个选项是正确的)
1.-3的绝对值是--------------------------------------------------------------------------------------------( )
A.-3 B.![]() C.
C.![]() D.3
D.3
2.下列运算中,结果正确的是----------------------------------------------------------------------------( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.在平面直角坐标系中,点P(-2,3)关于x轴的对称点在---------------------------------( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4. 在一个暗箱里放入除颜色外其他都相同的3个红球和11个黄球,搅拌均匀后随机任取一个球,取到是红球的概率是--------------------------------------------------------------------------( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.抛物线![]() 的顶点坐标是------------------------------------------------------------( )
的顶点坐标是------------------------------------------------------------( )
A.(3,2) B.(3,-2) C.(-3,-2) D.(-3,2)
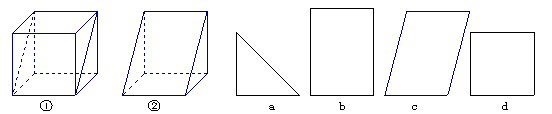 6.如图①是一个正方形毛坯,将其沿一组对面的对角线切去一半,得到一个工件如图②,对于这个工件,左视图、俯视图正确的一组是-----------------------------------------------------( )
6.如图①是一个正方形毛坯,将其沿一组对面的对角线切去一半,得到一个工件如图②,对于这个工件,左视图、俯视图正确的一组是-----------------------------------------------------( )
A.a、b B.b、d C.a、c D.a、d
7.在相同时刻的物高与影长成比例.小明的身高为1.5米,在地面上的影长为2米,同时一古塔在地面上的影长为40米,则古塔的高为-----------------------------------------------------( )
A.60米 B.40米 C.30米 D.25米
8.反比例函数![]() 的图象经过点(tan45°,cos60°),则k的值为---------------------( )
的图象经过点(tan45°,cos60°),则k的值为---------------------( )
A.2
B.1
C.![]() D.
D.![]()
9.已知圆锥的底面半径是3, 高为4, 则这个圆锥侧面展开图的面积是----------------------( )
A.12π B.15π C.20π D.24π
10.在同一平面内,△ABC与△A1B1C1关于直线m对称,△A1B1C1与△A2B2C2关于直线n对称,且有m∥n,则△ABC可以通过一次变换直接得到△A2B2C2,这个变换是-----( )
A.对称变换 B.平移变换 C.旋转变换 D.位似变换
11.如图1,小正方形的边长均为1,则下列图2中的三角形(阴影部分)与△ABC相似的是( )

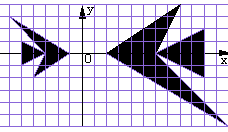
12.某学习小组在讨论“变化的鱼”时,知道大鱼和
小鱼是位似图(如图所示),则小鱼上的点(a,b)
对应大鱼上的点( )
A.(-2a,-2b) B.(-a,-2b)
C.(-2,-2a) D.(-2a,- b)
二.填空题(每小题5分,共30分)
13.化简:![]() =
.
=
.
 14.请写一个图象经过原点的函数解析式:
.
14.请写一个图象经过原点的函数解析式:
.
15.一元二次方程![]() 的解是:
.
的解是:
.
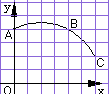
16.如图,直角坐标系中一条圆弧经过网格点A、B、C,其中B点
坐标为(4,4),则该圆弧所在圆的圆心坐标是 .
17.某住宅小区4月份随机抽查了该小区6天的用水量(单位:吨),结果分别是30、34、32、37、28、31,那么请你估计该小区4月份(30天)的总用水量约是 吨.
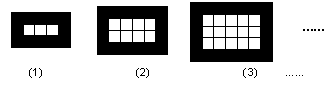
18.如图,用同样规格的黑、白两色正方形瓷砖铺设矩形地面,请观察,第n个图形中需要黑色瓷砖 块(用含n的代数式表示).
三.解答题 (共72分)
19.(8分) (1)计算: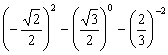 ;
;
(2)先化简,再求值:![]() ,其中
,其中![]() .
.
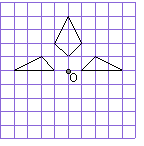
20.(8分)如图网格中有一个四边形和两个三角形.
(1)请你画出三个图形图形关于点O的中心对称图形;
(2)将(1)中画出的图形与原图形看成一个整体图形,
这个整体图形共有 条对称轴;
把这个整体图形绕点O至少旋转 度可与自身重合.
21.(10分)如图,已知点C、D在线段AB上,PC=PD,请你添加一个条件,使图中存在全等三角形,并给予证明.
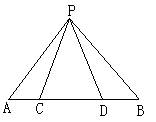 你所添加的条件为
;
你所添加的条件为
;
你得到的一对全等三角形是△ ≌△ .
证明:
22.(10分) 已知方程![]() 的解是x=3,求不等式
的解是x=3,求不等式![]() 的解集;
的解集;
(1) 解方程组: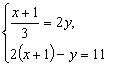 .
.
23.(10分)在杭金衢高速公路上,一辆轿车和一辆货车沿相同路线从A地到B地,所经过的路程y(千米)与时间x(小时)的函数关系图象如图所示,试根据图象,回答下列问题:
(1) 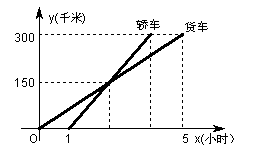 货车比轿车早出发
小时,
货车比轿车早出发
小时,
轿车追上货车时行驶了 千米,
A地到B地的距离为 千米;
(2) 轿车追上货车用了多少时间?
(3) 轿车比货车早到了多少时间?
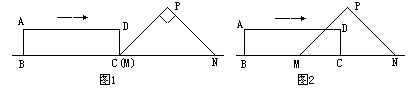
24.(12分)如图,Rt△PMN中,∠P=90°,PM=PN,MN=8cm,矩形ABCD的长和宽分别为8cm和2cm,C点和M点重合,BC和MN在一条直线上.令Rt△PMN不动,矩形ABCD沿MN所在直线向右以每秒1cm的速度移动,直到C点与N点重合为止.设移动x秒后,矩形ABCD与△PMN重叠部分的面积为ycm2,求y与x之间的函数关系式.
25.(14分) 如图,在直角坐标系中,正方形OABC的边长为2cm,点A、C分别在y轴的负半轴和x轴的正半轴上,抛物线![]() 经过点A、B,且
经过点A、B,且![]() .
.
(1) 求抛物线的解析式;
(2) 如果点P由点A开始沿AB边以2cm/s的速度向点B移动,同时点Q由点B开始沿BC边以1cm/s的速度向点C移动:
① 移动开始后第t秒时,设S=PQ2(cm2),试写出S与t之间的函数关系式,并写出t的取值范围;
②
 当S取得最小值时,在抛物线上是否存在点R,使得以P、B、Q 、R为顶点的四边形是平行四边形?如果存在,求出R点的坐标;如果不存在,请说明理由.
当S取得最小值时,在抛物线上是否存在点R,使得以P、B、Q 、R为顶点的四边形是平行四边形?如果存在,求出R点的坐标;如果不存在,请说明理由.