中考模拟数学试卷（四）
第Ⅰ卷（机读卷 共44分）
| 考生须 知 | 1. 本试卷分为第Ⅰ卷(机读卷)和第Ⅱ卷(非机读卷)两部分，共8页. 2. 认真填写密封线内的学校、姓名和考号. |
| 注意事 项 | 1. 考生要按要求在机读答题卡上作答，题号要对应，填涂要规范. 2. 考试结束，将试卷和机读答题卡一并交回. |
| 题 号 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 八 | 九 | 总 分 | |
| 得 分 |
| ||||||||||
| 阅卷人 |
| ||||||||||
一、选择题（本题共有11个小题，每小题4分，共44分）在每个小题给出的四个备选答案中，只有一个是符合题意的.
1. 计算－1－（－5）的结果是【 】
（A）－6 （B）4 （C） 6 （D）－4
2. 9的算术平方根是 【 】
（A）±3 （B）
（C）3 （D）－3
3. 如果内切两圆的半径分别为4cm和6cm , 则两圆的圆心距为 【 】
（A）2cm （B） 5cm （C）10cm （D）20cm
4. 光年是天文学中的距离单位，1光年约是km，用科学计数法表示为【 】
（A）
km （B）
km （C）
km （D）
km
5. 已知：一个正多边形的每一个内角都等于120°，则这个多边形是【 】
（A）正八边形 （B）正六边形 （C）正五边形 （D）正方形
6．已知点P（m，－n）和点Q（－m，n），那么点P和点Q 【 】
（A）关于x轴对称 （B）关于y轴对称
（C）关于原点对称 （D）以上结论都不对
7. 在△ABC中，若∠C= 90°，AC=1，BC=2，则下列结论中正确的是【 】
(A)
(B) 
(C)
(D)
8. 下列计算中不正确的是 【 】
（A）(－2)0=1 （B）2－1=－2 （C）(a+b)2=a2+2ab+b2 （D）2a2·3a3=6a5
9．函数y=
中，自变量x的取值范围是【 】
（A）x＞－2且x≠1 （B）x≥2且x≠1 （C）x≥－2且x≠1 （D）x≠1
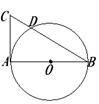10. 如图，AB为⊙O的直径，CA切⊙O于A，CB交⊙O于D，
若CD=2，BD=6，则⊙O直径的长为【 】
（A）
（B）
（C）
（D）
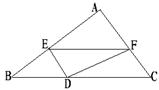
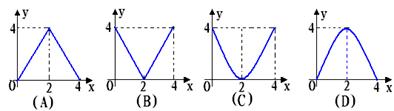11. 如图，已知△ABC中，BC=8，BC边上的高h=4，D为BC边上一个动点，EF∥BC，交AB于点E，交AC于点F，设E到BC的距离为x，△DEF的面积为y，则y关于x的函数图象大致为【 】
第Ⅱ卷（非机读卷共76分）
二、填空题：（本题共5个小题，每小题4分，共20分）
12. 如果m与－2互为倒数，那么m的值是 .
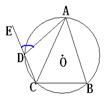13. 如图所示，四边形ABCD内接于⊙O，AB=AC，E是CD延长线上一点，
∠BAC=40○，则∠ADE的度数为 .
14. 某校初三(8)班有45名学生，其年龄统计结果如下表所示：
| 年 龄（岁） | 15 | 16 | 1 7 |
| 人 数 | 15 | 24 | 6 |
则这个班学生年龄的众数是 .
15. 把x2＋9加上一个单项式，使其成为一个完全平方式．请你写出1个符合条件
的单项式 ．
16. 等腰三角形一腰上的中线把等腰三角形的周长分成12和10两部分，则腰长为 .
三、细心解答下列各题：（本题共3个小题，每小题5分，共15分）
17. 分解因式：16－x2－y2＋2xy.
解：
18. 计算：
解：
19. 用换元法解方程 
.
解：
四、（本题满分5分）
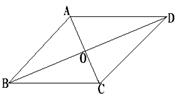20．如图，在四边形ABCD中，AD∥BC，对角线AC与BD相交于点O，AC平分∠BAD，请你再添一个什么条件? 就能推出四边形ABCD是菱形，并给出证明.
五、（本题满分6分）
21. 如图，一天晚上，李杨在广场上乘凉. 图中线段AB表示站在广场上的李杨，线段PO表示直立在广场上的灯杆，点P表示照明灯.
⑴请你在图中画出李杨在照明灯（P）照射下的影子；
⑵如果灯杆高PO=12m，李杨的身高AB=1.6m，李杨与灯杆的
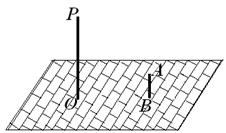距离BO=13m，请求出李杨影子的长度.
解：
六、（本题满分 6分）
22. 列方程或方程组解应用题：
为加快农村小城镇建设，某镇经过规划设计，有80万平方米的街道和空地需要改造和绿化，如果街道铺设柏油和空地绿化面积各占50%，则需要投资30万元，如果街道铺设柏油占40%，空地绿化占60%，则需要投资28万元，问每铺设街道柏油和空地绿化1万平方米各需要投资多少万元？
解：
七、（本题满分7分）
23. 已知：关于x的两个方程x2＋(m＋1)x＋m－5=0……①与mx2＋(n－1)x＋m－4=0…②，
方程①有两个不相等的负实数根，方程②有两个实数根.
（1）求证方程②的两根符号相同；
（2）设方程②的两根分别为α、β，若α ∶β=1∶3, 且n为整数，求m的最小整数值.
八、（本题满分8分）
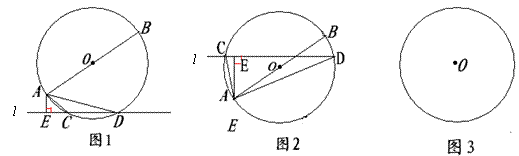
24. 如图1：AB是⊙O的直径，直线l交⊙O于C、D两点，AE⊥直线l，垂足为E.
（1）求证：AC·AD=AB·AE；
（2）若将直线l向上平移（如图2），交⊙O于C，D，使弦CD与直径AB相交（交点不与A、B重合），其他条件不变，请问（1）问的结论是否还成立？若成立，请给出证明，若不成立，请说明理由；
（3）若将直线l平移到与⊙O相切时，切点为M，其他条件不变，请你在图3上画出变化后的图形，标出相应字母，试猜想：AM、AB、AE的关系是什么？（只写出关系式，不要求证明）.
九、（本题满分9分）
25. 抛物线y=ax2＋bx＋c (a＜0)交x轴于点A(－3，0)、B（1，0），交y轴于点C，顶点为P，以PA为直径的⊙D恰好过点C.
(1)求点P、C、D的坐标 (用含a的代数式表示) ；
(2)求抛物线的解析式；
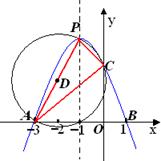(3)抛物线上是否存在一点Q，使△QPA为直角三角形？
若存在,求出点Q的坐标；若不存在,请说明理由.
解: