中考模拟自测题2
22．（本题满分10分）
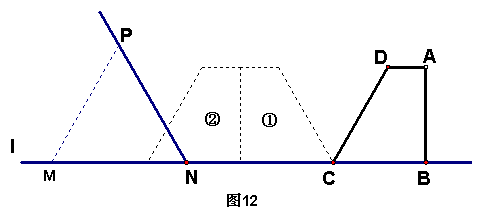
已知：如图12，在直角梯形ABCD中，AD∥BC，BC＝5cm，CD＝6cm，∠DCB＝60°，∠ABC＝90°。等边三角形MPN（N为不动点）的边长为
cm，边MN和直角梯形ABCD的底边BC都在直线
上，NC＝8cm。将直角梯形ABCD向左翻折180°，翻折一次得到图形①，翻折二次得图形②，如此翻折下去。
（1）将直角梯形ABCD向左翻折二次，如果此时等边三角形的边长a≥2cm，这时两图形重叠部分的面积是多少？
（2）将直角梯形ABCD向左翻折三次，如果第三次翻折得到的直角梯形与等边三角形重叠部分的面积等于直角梯形ABCD的面积，这时等边三角形的边长a至少应为多少？
（3）将直角梯形ABCD向左翻折三次，如果第三次翻折得到的直角梯形与等边三角形重叠部分的面积等于直角梯形面积的一半，这时等边三角形的边长应为多少？
22、福州市解：（1）重叠部分的面积等于
（2）等边三角形的边长a至少为10cm（3）等边三角形的边长为
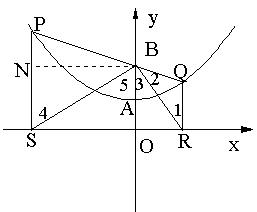
24．（本题满分12分）如图1，已知抛物线的顶点为A(O，1)，矩形CDEF的顶点C、F在抛物线上，D、E在
轴上，CF交y轴于点B(0，2)，且其面积为8．
(1)求此抛物线的解析式；
(2)如图2，若P点为抛物线上不同于A的一点，连结PB并延长交抛物线于点Q，过点P、Q分别作轴的垂线，垂足分别为S、R．
①求证：PB＝PS；
②判断△SBR的形状；
③试探索在线段SR上是否存在点M，使得以点P、S、M为顶点的三角形和以点Q、R、M为顶点的三角形相似，若存在，请找出M点的位置；若不存在，请说明理由．
24、.⑴解：方法一：
∵B点坐标为(0．2)，
∴OB＝2，
∵矩形CDEF面积为8，∴CF=4.∴C点坐标为(一2，2)．F点坐标为(2，2)。
设抛物线的解析式为
．其过三点A(0，1)，C(-2．2)，F(2，2)。
得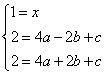
解这个方程组，得
∴此抛物线的解析式为 
………… (3分)
方法二：
∵B点坐标为(0．2)，∴OB＝2，
∵矩形CDEF面积为8，∴CF=4.∴C点坐标为(一2，2)。 ……… (1分)
根据题意可设抛物线解析式为
。 其过点A(0，1)和C(-2．2)
……… 解这个方程组，得
此抛物线解析式为
(2)解：
①过点B作BN
，垂足为N．
∵P点在抛物线y=
十l上．可设P点坐标为
．
∴PS＝
，OB＝NS＝2，BN＝。
∴PN=PS—NS=
………………………… (5分)
在Rt
PNB中．
PB＝
∴PB＝PS＝………………………… (6分)
②根据①同理可知BQ＝QR。
∴
，
又∵ 
，
∴
，
同理
SBP＝
………………………… (7分)
∴
∴
∴
.
∴ △SBR为直角三角形．………………………… (8分)
错误！未找到引用源。方法一：
设
，
∵由①知PS＝PB＝b．
，
。
∴
∴
。………………………… (9分)
假设存在点M．且MS＝，别MR＝
。
若使△PSM∽△MRQ，
则有
。
即
∴
。
∴SR＝2
∴M为SR的中点.………………………… (11分)
若使△PSM∽△QRM，
则有
。
∴
。
∴
。
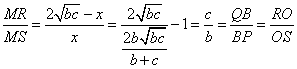∴M点即为原点O。
综上所述，当点M为SR的中点时．
PSM∽MRQ；当点M为原点时，PSM∽MRQ．………………………… (13分)
方法二：
若以P、S、M为顶点的三角形与以Q、M、R为顶点的三角形相似，
∵
，
∴有PSM∽MRQ和PSM∽△QRM两种情况。
当PSM∽MRQ时．SPM＝RMQ，SMP＝RQM．
由直角三角形两锐角互余性质．知PMS+QMR＝
。
∴
。………………………… (9分)
取PQ中点为N．连结MN．则MN＝
PQ=
．……………… (10分)
∴MN为直角梯形SRQP的中位线,
∴点M为SR的中点 …………………… (11分)
当△PSM∽△QRM时，
又
，即M点与O点重合。
∴点M为原点O。
综上所述，当点M为SR的中点时，PSM∽△MRQ；
当点M为原点时，PSM∽△Q RM……………………… (13分)
24．（本题满分12分）
如图15，点
在
轴上，
交轴于
两点，连结
并延长交于
，过点的直线
交轴于
，且的半径为
，
．
（1）求点
的坐标；
（2）求证：
是的切线；
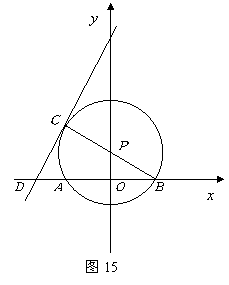（3）若二次函数
的图象经过点
，求这个二次函数的解析式，并写出使二次函数值小于一次函数值的的取值范围．
24、
解：（1）如图4，连结
······································································ 1分
，
······································· 2分
是的直径
（也可用勾股定理求得下面的结论）
，
················································· 3分
，
，
（写错一个不扣分）········································ 4分
（2）
过点
·········································· 5分
当
时，
··········································· 6分
，
（也可用勾股定理逆定理证明）······························· 7分
是的切线······················································································· 8分
（3）
过
点
···························································· 9分
························································································· 10分
24．（本题满分12分）
已知抛物线y=x2+(2n-1)x+n2-1 (n为常数).
(1)当该抛物线经过坐标原点，并且顶点在第四象限时，求出它所对应的函数关系式；
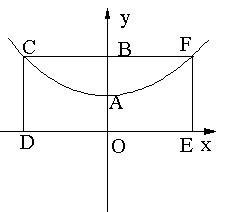
(2)设A是(1)所确定的抛物线上位于x轴下方、且在对称轴左侧的一个动点，过A作x轴的平行线，交抛物线于另一点D，再作AB⊥x轴于B，DC⊥x轴于C.
①当BC=1时，求矩形ABCD的周长；
②试问矩形ABCD的周长是否存在最大值？如果存在，请求出这个最大值，并指出此时A点的坐标；如果不存在，请说明理由
24、解：（1）由已知条件，得：n2－1=0
解这个方程，得： n1=1 ，n2=－1；
当n=1时，得y=x2+x，此抛物线的顶点不在第四象限；
当n=－1时，得y=x2－3x，此抛物线的顶点在第四象限；
∴所求的函数关系式为y=x2－3x …… (4分)
(2)由y=x2－3x，令y=0，得x2－3x=0，解得x1=0 ，x2=3；
∴抛物线与x 轴的另一个交点为（3，0）
∴它的顶点为（
），对称轴为直线x=
①∵BC=1，由抛物线和矩形的对称性易知OB=
∴B（1，0）
∴点A的横坐标x=1，又点A在抛物线y=x2－3x上，
∴点A的纵坐标y=12－3×1=－2。
∴AB=y =2
∴矩形ABCD的周长为：2（AB+BC）=6 …… (8分)
②∵点A在抛物线y=x2－3x上，可以设A点的坐标为（x，x2－3x），
∴B点的坐标为 （x，0）。（0＜x＜
∴BC=3－2x，A在x 轴的下方，
∴x2－3x＜0
∴AB= x2－3x =3x－x2
∴矩形ABCD的周长P=2〔（3x－x2）+（3—2x）〕=－2（x－
）2+
∵a=－2＜0
∴当x=时， 矩形ABCD的周长P最大值是。 …… (12分)
23．（本题满分11分）
如图16，在平面直角坐标系中，矩形ABCO的面积为15，边OA比OC大2．E为BC的中点，以OE为直径的⊙O′交轴于D点，过点D作DF⊥AE于点F．
（1） 求OA、OC的长；
（2） 求证：DF为⊙O′的切线；
（3） 
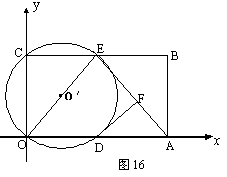小明在解答本题时，发现△AOE是等腰三角形．由此，他断定：“直线BC上一定存在除点E以外的点P，使△AOP也是等腰三角形，且点P一定在⊙O′外”．你同意他的看法吗？请充分说明理由．
解：
23、解： （1）在矩形OABC中，设OC=x 则OA= x+2，依题意得
解得：
（不合题意，舍去） ∴OC=3， OA=5
… (4分)
（只要学生写出OC＝3，OA＝5即给2分）
（2）连结O′D 在矩形OABC中，OC=AB，∠OCB=∠ABC=90
，CE=BE=
∴ △OCE≌△ABE ∴EA=EO ∴∠1=∠2
在⊙O′中， ∵ O′O= O′D ∴∠1=∠3
∴∠3=∠2 ∴O′D∥AE，
∵DF⊥AE ∴ DF⊥O′D
又∵点D在⊙O′上，O′D为⊙O′的半径 ，
∴DF为⊙O′切线。 … (8分)
(3) 不同意. 理由如下:
25 当AO=AP时，
以点A为圆心，以AO为半径画弧交BC于P1和P4两点
过P1点作P1H⊥OA于点H，P1H = OC = 3，∵A P1= OA = 5
∴A H = 4， ∴OH =1 求得点P1（1，3） 同理可得：P4（9，3） …… (9分)
②当OA=OP时，
同上可求得:：P2（4，3），P3（
4，3）
…… (11分)
 |
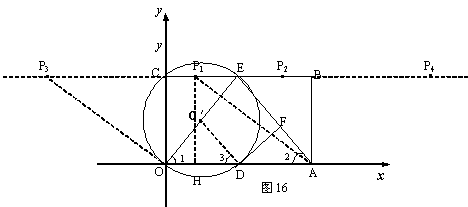因此，在直线BC上，除了E点外，既存在⊙O′内的点P1，又存在⊙O′外的点P2、P3、P4，它们分别使△AOP为等腰三角形。 …… (12分)
24．（本题满分12分）
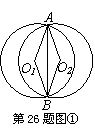
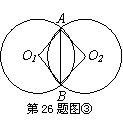
如图①、②、③是两个半径都等于2的⊙O1和⊙O2，由重合状态沿水平方向运动到互相外切过程中的三个位置，⊙O1和⊙O2相交于A、B两点，分别连结O1A、O1B、O2A、O2B和AB。
（1）如图②，当∠AO1B=120°时，求两圆重叠部分图形的周长l；(4分)
（2）设∠AO1B的度数为x，两圆重叠部分图形的周长为y，求y关于x的函数关系式，并写出自变量x的取值范围；(4分)
（3）由(2)，若y=2x，则线段O2A所在的直线与⊙O1有何位置关系？为什么？除此之外，它们还有其它的位置关系，写出其它位置关系时x的取值范围。(4分)
 | |||||
 |  | ||||
24.如图，点A在Y轴上，点B在X轴上，且OA=OB=1，经过原点O的直线L交线段AB于点C，过C作OC的垂线，与直线X=1相交于点P，现将直线L绕O点旋转，使交点C从A向B运动，但C点必须在第一象限内，并记AC的长为t，分析此图后，对下列问题作出探究：
（1）当△AOC和△BCP全等时，求出t的值。
（2）通过动手测量线段OC和CP的长来判断它们之间的大小关系？并证明你得到的结论。
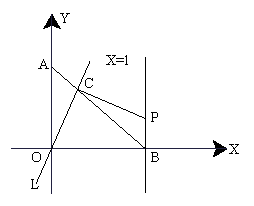（3）①设点P的坐标为（1,b）,试写出b关于t的函数关系式和变量t的取值范围。②求出当△PBC为等腰三角形时点P的坐标。
24．（1）t=
（3分）
（2）OC=CP （4分）
过点C作X轴的平行线，交OA与直线BP于点T、H，
证△OTC≌△CHP即可 （7分）
（3）①
（0≤t≤1）
（10分）
②当t=0或1时，△PBC为等腰三角形，
即P（1.1）, P（1，1－
） （12分 ）
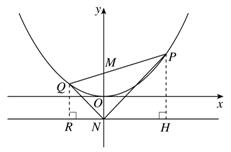
17．（本小题满分10分）．已知点M，N的坐标分别为（0，1），（0，－1），点P是抛物线
上的一个动点．（1）求证：以点P为圆心，PM为半径的圆与直线
的相切；
（2）设直线PM与抛物线的另一个交点为点Q，连接NP，NQ，求证：
．
17、（本小题满分10分）
解：（1）设点P的坐标为
，则
PM＝
;
又因为点P到直线的距离为
，
所以，以点P为圆心，PM为半径的圆与直线相切．
（得4分）
（2）如图，分别过点P，Q作直线的垂线，垂足分别为H，R．由（1）知，PH＝PM，同理可得，QM＝QR．
因为PH，MN，QR都垂直于直线，所以，PH∥MN∥QR，于是
，
所以
，
因此，Rt△
∽Rt△
．
于是
，从而 （得6分）
24． 
如图，已知AB是⊙O的直径，AC是⊙O的弦，点D是弧ABC中点，弦DE⊥AB，垂足为F，DE交AC于点G.
（1）图中有哪些相等的线段？（要求：不再标注其他字母，找结论的过程中所作的辅助线不能出现在结论中，不写出推理过程）
（2）若过点E作⊙O的切线ME，交AC的延长线于点M（请补完整图形），试问：ME=MG是否成立？若成立，请证明；若不成立，请说明理由.
（3）在满足第（2）问的条件下，已知AF=3，FB=
，求AG与GM的比.〖第（1）的结论可直接利用〗
24．解. （1）OA=OB，DF=EF，DE=AC，AG=DG，EG=CG. ………………………………3分
（2）ME=GM. 理由是：连EO并延长交⊙O于点N，连结DN.
∵EM是⊙O的切线，
∴∠OEM=90º，∴∠GEM+∠GEN=90º. …………………………………………5分
∵EN是⊙O的直径，∠N+∠GEN=90º，
∴∠N=∠GEM. ………………………………………………………………7分
∵AB是⊙O的直径，∴∠B+∠BAC=90º，
∵∠AGF+∠GAF=90º，∴∠AGF=∠B，……………………………………9分
∵∠AGF=∠CGE，∴∠CGE=∠B.
∵AC=DE，∴∠N=∠B，
∴∠GEM=∠CGE，∴MG=ME. ………………………………………………11分
（3）答案：
.…………………………………………………………………14分
28（本题满分12分）
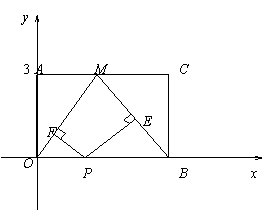
如图：矩形的顶点在坐标原点O，OA在y轴上，A点坐标为（0，3），另一边OB在x的正半轴上,点M是AC边的中点，点P是OB边上一动点,PF⊥OM，PE⊥BM，垂足分别为E、F．
（1）若四边形PEMF为矩形，求B点坐标；
（2）在（1）的条件下，求过A、M、B三点的抛物线解析式；
（3）在抛物线上是否存在一点N，使得四边形AMON是平行四边形，若存在，求出点N的坐标，若不存在，说明理由。
28.（1）B（6，0）………………………………4分
（2）
………………………………8分
（3）存在。N（－3，0）………………………………12分
31．（本小题12分）
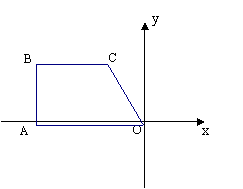
如图，梯形OABC中，BC∥AO，∠BAO=90°，B（－3
，3），直线OC的解析式为
y=－x，将ΔOBC绕点C顺时针旋转60°后，O到O1，B到B1，得ΔO1B1C.
（1）求证：点O1在x轴上；
（2）将点O1运动到点M（－4，0），求∠B1MC的度数；
（3）在（2）的条件下，将直线MC向下平移m个单位长度，设直线MC与线段AB交于点P，与线段OC的交于点Q，四边形OAPQ的面积为S，求S与m的函数关系式，并求出m的取值范围.
 |
解：（1）由题意：C（－，3）
∴tan∠COA=
∴∠COA=60°
∵∠OCO1=60°，CO=CO1
∴ΔCOO1为等边三角形
∴∠COO1=60°
∴∠COA=∠COO1
∴点O1在x轴上. ……4’
∵∠COO1=60°，BC∥AO
（2）∠BCO=120°
∴BCO1=120°
∵∠O1CO=60°
∴∠BCO=180°
∴B、C、O三点共线
∴C（－，3）
∴CO=CO1=O1O=2
∵M1O=4
∴M1O1=O1O=O1C
可证得 ∠M1CO=90°
∵BC=CO=2
BC=B1C
∴B1C=CO
∴M1B=M1O
∴∠BM1C=∠B1M1O=30° ……8’
（2） ∵AD=1，PD=m
∴AP=1－m
在ΔCEQ中，CE=m，∠ECQ=30°
∴CQ=
m
∴OQ=2－m
∴QN=3－
m，ON=－
m
∴AN=2+m
又∵S四边形OAPQ=S梯形PAQN+SΔQNO
∴S=[(1―m)+(3―m)][2+m]+(―m)(3―m)
∴S=―
m2―2m+
(0<m<1) ……12’