九年级第一次模拟检测数 学 试 卷
本试卷分卷Ⅰ和卷Ⅱ两部分;卷Ⅰ为选择题,卷Ⅱ为非选择题.
本试卷满分为120分,考试时间为120分钟.
卷Ⅰ(选择题,共20分)
注意事项:1.答卷I前,考生务必将自己的姓名、准考证号、科目填涂在答题卡上,考试结束,监考人员将试卷和答题卡一并收回.
2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑.答在试卷上无效.
一、选择题(本大题共10个小题;每小题2分,共20分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.在平面直角坐标系中,下列各点在第二象限的是
A.(2,1) B.(2,-1) C.(-2,1) D.(-2,-1)
2.某种感冒病毒的直径是0.米,用科学记数法表示这个数的结果为
A.12×10-7 B.1.2×10-6 C.1.2×10-7 D.1.2×10-8
3.如图,是由6个相同的小立方块搭成的几何体,那么这个几何体的俯视图是
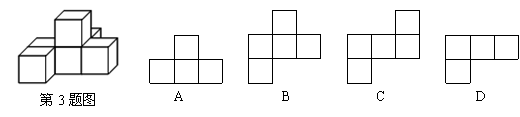
4.分解因式x3—x,结果为
A.x(x2—1) B.x(x—1)2 C.x(x+1)2 D.x(x+1)(x—1)
5.哥哥身高1.68米,在地面上的影子长是2.1米,同一时间测得弟弟的影子长1.8米,则弟弟身高是
A.1.44米 B.1.52米 C.1.96米 D.2.25米
6.已知圆锥的侧面展开图的面积是15πcm2,母线长是5cm,则圆锥的底面半径长
A.1.5cm B.3cm C.4cm D.6cm
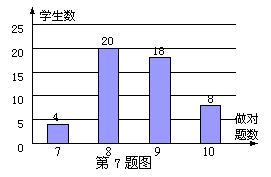 7.数学老师布置10道题作为课堂练习,课代表将全班同学的答题情况绘制成条形统计图(如图),根据图表,全班每位同学答对的题数所组成样本的中位数和众数分别为
7.数学老师布置10道题作为课堂练习,课代表将全班同学的答题情况绘制成条形统计图(如图),根据图表,全班每位同学答对的题数所组成样本的中位数和众数分别为
A.8,8 B.8,9
 C.9,9
D.9,8
C.9,9
D.9,8
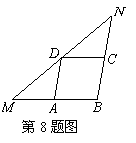
8.如图,在△MBN中,BM=6,点A,C,D分别在MB,NB,MN上,四边形ABCD为平行四边形,且∠NDC=∠MDA,则平行四边形ABCD的周长是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
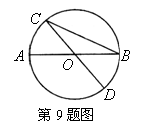 9.如图,AB和CD都是⊙O的直径,∠AOC=50°,则∠C 的度数是
9.如图,AB和CD都是⊙O的直径,∠AOC=50°,则∠C 的度数是
A.20° B.25°
C.30° D.50°
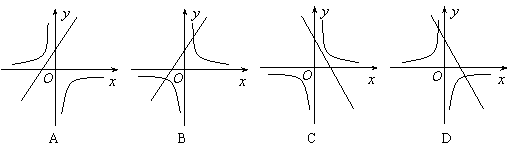
10.在同一直角坐标系中,函数![]() 与
与![]() 的 图象大致是
的 图象大致是
 |
| 总分 | 核分人 |
九年级第一次模拟检测数 学 试 卷
卷II(非选择题,共100分)
注意事项:1.答卷II前,将密封线左侧的项目填写清楚.
2.答卷II时,将答案用蓝色、黑色钢笔或圆珠笔直接写在试卷上.
| 题 号 | 二 | 三 | |||||||
| 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | ||
| 得 分 | |||||||||
| 得分 | 阅卷人 | 二、填空题(本大题共8个小题;每小题3分,共24分.把答案写在题中横线上) |
11.-6的绝对值是 .
 12.在函数
12.在函数![]() 中,自变量
中,自变量![]() 的取值范围是
.
的取值范围是
.
13.抛物线![]() 的顶点坐标是
______.
的顶点坐标是
______.
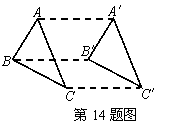
 14.如图,△ABC平移到△A′B′C′,则图中与线段AA′平行且相等的线段有
条.
14.如图,△ABC平移到△A′B′C′,则图中与线段AA′平行且相等的线段有
条.
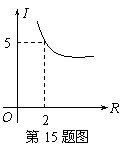
15.在某一电路中,保持电压不变,电流![]() (安)与电阻R(欧)成反比例关系.其函数图像如图所示,则这一电路的电压为
(安)与电阻R(欧)成反比例关系.其函数图像如图所示,则这一电路的电压为
伏.
16.某同学参加了5次考试,平均成绩是68分,他想在下一次考试后使六次考试的平均成绩不低于70分,那么他第六次考试至少要得 分.
 17.把一枚均匀的硬币连续抛掷2次,“至少有一次硬币正面朝上”的概率是__________.
17.把一枚均匀的硬币连续抛掷2次,“至少有一次硬币正面朝上”的概率是__________.
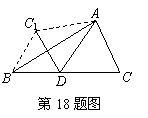
18.如图,AD是△ABC的中线,∠ADC=60,把△ADC沿直线AD折过来,点C落到点C1的位置,如果BC=4,那么BC1= .
三、解答题(本大题共8个小题;共76分)
| 得分 | 阅卷人 | 19.本题8分 |
化简求值:![]() ,其中x=-3
,其中x=-3
| 得分 | 阅卷人 | 20.本题8分 |
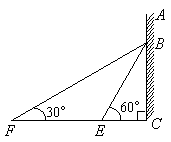
如图,在某建筑物AC上,挂着一条宣传条幅BC,小明站在点F处,看条幅顶端B,测得仰角为30°;再往条幅方向前行20米到达点E处,看条幅顶端B,测得仰角为
60°,求宣传条幅BC的长.(小明的身高忽略不计)
 |
| 得分 | 阅卷人 | 21.本题8分 |
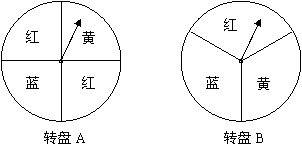
小明和小芳做一个“配色”的游戏.如图是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形,并涂上图中所示的颜色.同时转动两个转盘,如果转盘A转出了红色,转盘B转出了蓝色(或者转盘A转出了蓝色,转盘B转出了红色),则红色和蓝色在一起配成紫色,这种情况下小芳获胜;同样,蓝色和黄色在一起配成绿色,这种情况下小明获胜;在其它情况下,则小明、小芳不分胜负.
(1)利用列表或树状图的方法表示此游戏所有可能出现的结果;
(2)此游戏的规则,对小明、小芳公平吗?试说明理由.
 |
| 得分 | 阅卷人 | 22.本题8分 |
用两个全等的正方形ABCD和CDFE拼成一个矩形ABEF,把一个足够大的直角三角尺的直角顶点与这个矩形的边AF的中点D重合,且将直角三角尺绕点D按逆时针方向旋转.
(1)当直角三角尺的两直角边分别与矩形ABEF的两边BE,EF相交于点G,H时,如图甲,通过观察或测量BG与EH的长度,你能得到什么结论?并证明你的结论.
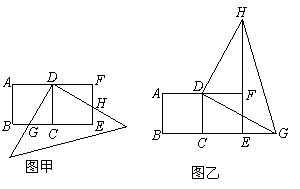 (2)当直角三角尺的两直角边分别与BE的延长线,EF的延长线相交于点G,H时(如图乙),你在图甲中得到的结论还成立吗?简要说明理由.
(2)当直角三角尺的两直角边分别与BE的延长线,EF的延长线相交于点G,H时(如图乙),你在图甲中得到的结论还成立吗?简要说明理由.
| 得分 | 阅卷人 | 23.本题10分 |
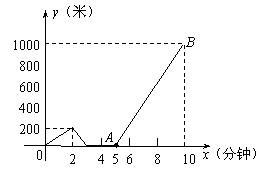
小文家与学校相距1000米.某天小文上学时忘了带一本书,走了一段时间才想起,于是返回家拿书,然后加快速度赶到学校.下图是小文与家的距离![]() (米)关于时间
(米)关于时间![]() (分钟)的函数图象.请你根据图象中给出的信息,解答下列问题:
(分钟)的函数图象.请你根据图象中给出的信息,解答下列问题:
(1)小文走了多远才返回家拿书?
(2)求线段AB所在直线的函数解析式;
 (3)当
(3)当![]() 分钟时,求小文与家的距离.
分钟时,求小文与家的距离.
| 得分 | 阅卷人 | 24.本题10分 |
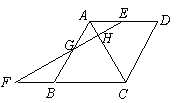 如图,四边形ABCD中,AD∥BC,AD=DC=BC,过AD的中点E作AC的垂线EF,垂足为H,EF交AB于点G,交CB的延长线于点F.
如图,四边形ABCD中,AD∥BC,AD=DC=BC,过AD的中点E作AC的垂线EF,垂足为H,EF交AB于点G,交CB的延长线于点F.
求证:(1)四边形ABCD是菱形.
(2)BF=DE.
| 得分 | 阅卷人 | 25.本题12分 |
一座隧道的截面由抛物线和长方形构成,长方形的长为8m,宽为2m,隧道最高点P位于AB的中央且距地面6m,建立如图所示的坐标系
(1)求抛物线的解析式;
(2)一辆货车高4m,宽2m,能否从该隧道内通过,为什么?
 (3)如果隧道内设双行道,那么这辆货车是否可以顺利通过,为什么?
(3)如果隧道内设双行道,那么这辆货车是否可以顺利通过,为什么?
| 得分 | 阅卷人 | 26.本题12分 |
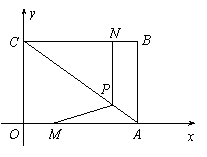
如图,在平面直角坐标系中,四边形OABC为矩形,点A,B的坐标分别为(4,0),(4,3),动点M,N分别从点O,B同 时出发,以每秒1个单位的速度运动,其中点M沿OA向终点A运动,点N沿BC向终点C运动,过点N作NP⊥BC,交AC于点P,连结MP,当两动点运动了![]() 秒时.
秒时.
(1)P点的坐标为( , )(用含![]() 的代数式表示).
的代数式表示).
(2)记△MPA的面积为S,求S与![]() 的函数关系式
的函数关系式![]() .
.
(3)当t为多少秒时,![]() 有最大值,最大值是多少.
有最大值,最大值是多少.
 (4)若点Q在
(4)若点Q在![]() 轴上,当S有最大值且△QAN为等腰三角形时,求直线AQ的解析式.
轴上,当S有最大值且△QAN为等腰三角形时,求直线AQ的解析式.