九年级数学4月份调研试卷
班级 学号 姓名 得分
一、选择题（本题有8小题，每小题3分，共24分．请选出各题中唯一的正确选项，不选、多选、错选，均不得分）
1．计算－1－（－5）的结果是【 】
（A）－6 （B）4 （C） 6 （D）－4
2． 9的算术平方根是 【 】
（A）±3 （B）
（C）3 （D）－3
3．据“保护长江万里行”考察队统计，仅2003年长江流域废水排放量已达163.9亿吨！治长江污染真是刻不容缓了！请将这个数据用四舍五入法，使其保留两个有效数字，再用科学记数法表示出来是【】
(A) 
亿吨 (B) 
亿吨 (C) 
亿吨 (D)
亿吨
4．下列计算中不正确的是 【 】
（A）(－2)0=1 （B）2－1=－2 （C）(a+b)2=a2+2ab+b2 （D）2a2·3a3=6a5
5． 若反比例函数
的图象经过点（-1 , 2 )，则这个函数的图象一定经过点【 】
(A)(2,-1)
(B)(
,2)
(C)(-2,-1) (D)(
,2)
6. 右边给出的是2006年3月份的日历表，任意
圈出一竖列上相邻的三个数，请你运用方程思想来研
究，发现这三个数的和不可能是【 】
(A) 69 (B) 54 (C) 27 (D)40
7．下列四个函数中，y随x增大而减小的是【 】
( A) y=2x (B) y=―2x+5 (C) y=―
(D) y=―x2+2x―1
如图是一次函数y1=kx+b和反比例函数y2=
的图象，
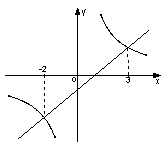8．观察图象写出y1＞y2时，
的取值范围【 】
（A）x＞3 （B）－2＜x＜0
（C）－2＜x＜0且x＞3 （D）－2＜x＜0或x＞3．
二、填空题（本题有8小题，每小题3分，共24分）
9．如果m与－2互为倒数，那么m的值是 .
10． 把x2＋9加上一个单项式，使其成为一个完全平方式．请你写出1个符合条件
的单项式 ．
11．关于x的不等式3x－2a≤－2的解集如图所示，则a的值是 .
12． 请你观察思考下列计算过程：
∵
∴
∵
∴
因此猜想：
＝
。
13．下列方程①
；②
；③
；④
中，无实根的方程是
。
14．计算
的结果是_ _；
15．函数y=
中，自变量x的取值范围是 .
16．某商场4月份随机抽查了5天的营业额，结果如下（单位：万元）：2.8，3.2，2.7，3.0，3.3，试估计该商场4月份的总营业额大约是 万元。
三、解答题（本题有8小题，前6小题，每小题6分，后2个小题每题8分，共52分）
17． 分解因式： 
.
18．计算：
19．课堂上老师给大家出了这样一道题：当
时，求代数式
的值，小明一算，发现计算结果相同，你能说明为什么吗？
20． 已知关于x的方程
的一个解与方程
的解相同。
⑴求k的值；
⑵求方程的另一个解.
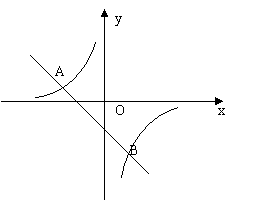
21．如图，一次函数
的图象与反比例函数
图象交于A（－2，1）、B（1，n）两点。
求n和一次函数的解析式;
 |
22．不透明的口袋里装有白、黄、蓝三种颜色的乒乓球（除颜色外其余都相同），其中白球有2个，黄球有1个，现从中任意摸出一个是白球的概率为.
（1）试求袋中蓝球的个数.
（2）第一次任意摸一个球（不放回），第二次再摸一个球，请用画树状图或列表格法，求两次摸到都是白球的概率.
23．浏阳河旅行社为吸引市民组团去张家界风景区旅游，推出如下收费标准：如果人数不超过25人，人均旅游费用为1000元；如果人数超过25人，每增加1人，人均旅游费用降低20元，但人均旅游费用不少于700元。某单位利用五一长假组织员工去张家界风景区旅游，共支付给旅行社旅游费用27000元。请问该单位这次共有多少员工去张家界风景区旅游？
24．某单位欲从内部招聘管理人员一名，对甲、乙、丙三名候选人进行了笔试和面试两项测试，三人的测试成绩如下表所示：
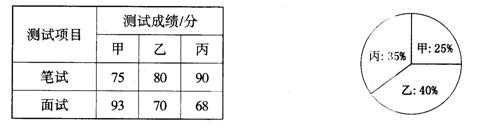
根据录用程序，组织200名职工对三人利用投票推荐的方式进行民主评议，三人得票率（没有弃权票，每位职工只能推荐1人）如上图所示，每得一票记作1分．
(l）请算出三人的民主评议得分；
(2）根据实际需要，单位将笔试、面试、民主评议三项测试得分按 4 : 3 : 3 的比例确定个人成绩，那么谁将被录用？
四、综合题(本题共2个小题，每小题10分，共20分)
25．某工厂现有甲种原料360千克，乙种原料290千克，计划利用这两种原料生产A、B两种产品共50件，已知生产一件A种产品用甲种原料9千克，乙种原料3千克，可获利700元；生产一件B种产品用甲种原料4千克，乙种原料10千克，可获利1200元。
（1）按要求安排A、B两种产品的生产件数，有哪几种方案？请你设计出来；
（2）设生产A、B两种产品总利润为
元，其中一种产品生产件数为件，试写出与之间的函数关系式，并利用函数的性质说明那种方案获利最大？最大利润是多少？
26．如图，P为轴正半轴上一点，半圆P交轴于A、B两点，交轴于C点，弦AE分别交OC、CB于点D、F，已知
。
（1）求证：AD＝CD；
（2）若DF＝
，tan∠ECB＝
，求经过A、B、C三点的抛物线的解析式；
（3）设M为轴负半轴上一点，OM＝
AE，是否存在过点M的直线，使该直线与（2）中所得的抛物线的两个交点到轴距离相等？若存在，求出这条直线的解析式；若不存在，请说明理由。
参考答案：
1~8： BCBB ADBD
9. 
；10、
；11、；12、 13、①；14、
；15、
16、90．
17、 
18.、
19、 化简后原式=1
20、（1）解得x=2，将x=2代入得k=-1；
（2）解
得
21、m=-2，n=-2；y=-x-1
22、解：⑴设蓝球个数为个
则由题意得
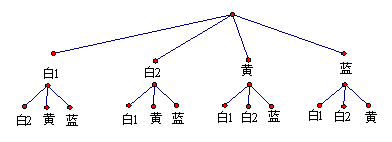答：蓝球有1个
∴ 两次摸到都是白球的概率 =
=
23、设这次去张家界旅游的员工有x人
解得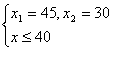
，
24、 解：(l)甲、乙、丙的民主评议得分分别为：50 分，80 分，70 分．
(2）如果将笔试、面试、民主评议三项测试得分按4 : 3 : 3的比例确定个人成绩，那么
甲的个人成绩为：
72.9（分）,
乙的个人成绩为：
77（分）
丙的个人成绩为：
77.4（分）
由于丙的个人成绩最高，所以候选人丙将被录用．
25、（1）设生产A种产品件，那么B种产品
件，则：
解得30≤≤32
∴＝30、31、32，依的值分类，可设计三种方案；
（2）设安排生产A种产品件，那么：
整理得：
（＝30、31、32）
根据一次函数的性质，当＝30时，对应方案的利润最大，最大利润为45 000元。
26、（1）连结AC；（2）
；（3）不存在