初中毕业生学业考试数学模拟试卷2

初中毕业生学业考试数学模拟试卷2

 (仁爱中学)

卷　一

一．选择题：（每小题3分，共36分）

1．如果与的和为O，那么是-----------------------------------------（　　）

A.2　 　　　　　　 B.　 　　　　 C.　　　　　 D.　　

2．随着中国综合国力的提升,近代来全球学习汉语的人数不断增加.据报道,2005年海外学习汉语的学生人数已达人,用科学记数法表示为（　　　）

　　A.3.82　　　　B. 　　C. 　　 D.

3．下列图形中不是轴对称图形的是(　　　)

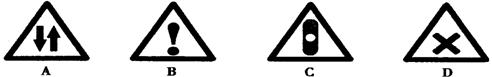4．由一些大小相同的小正方形组成的几何体三

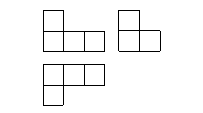视图如图所示，那么，组成这个几何体的小整

个正方体有　　　　　　　　　　  (　　　 )

A．6块　　　　　 B．5块　　　　　 

C．4块　　　　　 D．3块

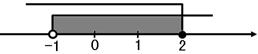
5．下列不等式组的解集，在数轴上表示为如图所示的是　（　　　）

Ａ．　　　  Ｂ．

Ｃ．　　　　Ｄ．　　　　　 

6． 晓晓根据下表，作了三个推理：

x	1	lO	100	1000	10000	…
	3	2.1	2．Ol	2.001	2.0001	…

　① (x>0)的值随着I的增大越来越小；

　② (x>0)的值有可能等于2；

　③  (x>O)的值随着x的增大越来越接近于2．

 则推测正确的有(　　　)

　A 0个　　B．1个　　C．2个　　D. 3个

7．某学校举行理科（含数学、物理、化学、生物四科）综合能力比赛，四科的满分都为100分．甲、乙、丙三人四科的测试成绩如下表：

学科	数学	物理	化学	生物
甲	95	85	85	60
乙	80	80	90	80
丙	70	90	80	95

综合成绩按照数学、物理、化学、生物四科测试成绩的的比例计分，则综合成绩的第一名是（　　　）

A．甲　　　　B．乙　　　C．丙　　　D．不确定

8．函数中，自变量x的取值范围是（　　　）

A. 　　　 B. 　　　　C . 　　　 D.

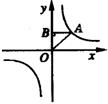9．如图，点A是y=图像上的一点，AB⊥y轴于点B，

则△AOB的面积是(　　　 )

A．1　　　　　B．2　　　　　　C．3　　　　　 D．4

第9题图形卡

10．如图，一次函数的图像经过A、B两点，

则解集是　  (　　　 )

第10题图形卡

A．　　　　 B．　　　　 

C．　　　　  D．

11 在一个不透明的布袋中，红色、黑色、白色的玻璃球共有40个，除颜色其他外完全相同，小李通过多次摸球试验后发现其中摸到红色、黑色球的频率分别为15%和45%，则口袋中白色球的数目很可能是 （　 ）

A．6　　　　 B．16　　　 C．18　　　　D．24

12．如图，在把易拉罐中水倒入一个圆水杯

的过程中，若水杯中的水在点P与易拉罐刚

好接触，则此时水杯中的水深为（　 ）。

A、2cm　　　　B、4cm　　　　

C、6cm　　　　D、8cm

卷　 二

二．填空题：（每小题3分，共21分）

13  已知6x－3y=16，并且5x＋3y=6，则4x－3y的值为　　　　。

第14题图形卡

14.如图，DE与△ABC的边AB，AC分别相交于D，E两点，且DE∥BC．

若DE＝2㎝，BC＝3㎝，EC＝㎝，则AC＝________㎝．

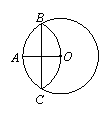
15.如图，⊙O的半径OA=6，以点A为圆心，OA为半径的弧交

第15题图形卡

⊙O于B，C两点，则BC等于　　　　　 。

16. 亮亮想制作一个圆锥模型，这个模型的侧面是用一个半径为9cm，圆心角为240°的扇形铁皮制作的，再用一块圆形铁皮做底。请你帮他计算这块铁皮的半径为________cm

17.如图，矩形AOCB的两边OC、OA分别位于x轴、y轴上，

点B的坐标为B（-，5），D是AB边上的一点，将△ADO

沿直线OD翻折，使A点恰好落在对角线OB上的点E处，若

第17题图形卡

点E在一反比例函数的图像上，那么该函数的解析式是_________．

18．有一块表面是咖啡色，内部是白色、形状是正方体

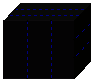的烤面包，用刀在它的上表面，前表面和右侧表面沿虚

线各切两刀（如图1），切成若干块小正方体面包（如图2），

 这些小正方体面包的表面只有白色与咖啡色两种，则表面是咖啡色的面有偶数个的小正方体个数是　　　　 .

(图2)

(图1)

(图1)

19.在实数的原有运算法则中,我们补充定义新运算”,

如下:当a≥b时,,当a<b时,则=

当-2≤x≤2时,的最大值为______.

三．解答题：第20～23题各6分，第24～26题各9分，第27题12分，共63分）

20．　　　　　 21．解方程：

22．今有甲，乙两人进行射击练习，成绩（命中环数）按先后次序记录如下：

甲	9	6	7	6	2	7	8	9	8	9
乙	3	4	6	8	7	8	8	8	9	10

试运用所学知识对甲，乙两人的成绩给予评判。（评判标准有三点以上者满分）

　　　　　　　　　　　　　　　　　　　　　　　　　　　　 

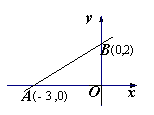
23．B港在离观测站A的正北10海里处, 一艘轮船从B港出发向东航行.观测站第一次测得该船在A地北偏东30°的M处,半小时后测得该船在A地北偏东60°的N处,求这艘轮船的速度。

　　　　　　　　　　　　　　　　　  北

东

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

A

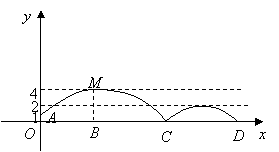
24．如图，足球场上守门员在处开出一高球，球从离地面1米的处飞出（在轴上），运动员乙在距点6米的处发现球在自己头的正上方达到最高点，距地面约4米高，球落地后又一次弹起．据实验测算，足球在草坪上弹起后的抛物线与原来的抛物线形状相同，最大高度减少到原来最大高度的一半．

（1）求足球开始飞出到第一次落地时，该抛物线的表达式．

（2）足球第一次落地点距守门员多少米？（取）

（3）运动员乙要抢到第二个落点，他应再向前跑多少米？（取）

www.1230.org 初中数学资源网 收集整理

25．已知：将一副三角板（Rt△DEF）如图1摆放，点E、A、D、B在一条直线上，且D是AB的中点，将Rt△DEF绕点D顺时针方向旋转角α（0°<α<90°）．在旋转过程中，直线DE、AC相交于点M，直线DF、BC相交于点N，分别过点M、N作直线AB的垂线，垂足为G、H．

　　（1）当α=30°时（如图2），求证：AG=DH；

　　（2）当α=60°时（如图3），（1）中的结论是否成立？请写出你的结论，并说明理由；

（3）当0°<α<90°时（如图4），（1）中的结论是否成立？请写出你的结论，并说明理由．

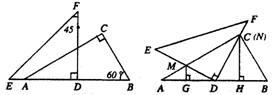
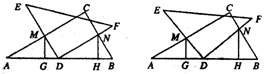
　　　　图1　　　　　　　　 图2　　　　　　  图3　　　　　　　　 图4

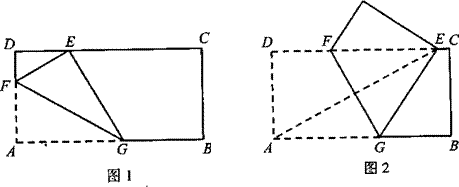
26.已知矩形纸片ABCD，AB=2，AD=1，将纸片折叠，使顶点A与边CD上的点E重合.

(1)如果折痕FG分别与AD、AB交于点F、G(如图1)，，求DE的长；

 (2)如果折痕FG分别与CD、AB交于点F、G(如图2)，△AED的外接圆与直线BC相切，

　求折痕FG的长．

27.如图平面直角坐标中，四边形OABC是梯形，BC∥OA,OA=7，AB=OC=4，BC=3，

　(1)求∠COA的度数；　　　　

　(2)若P点在坐标轴上，且P、O、C三点构成等腰三角形，求P坐标；(只要写出坐标即可)

(3)在(2)中条件下,任取其中三点使经过该三点的图像是以y轴为对称轴的抛物线,称为最佳组合,求任取三点是最佳组合的概率.

(4)若有一个角是60°的三角板,60°角的顶点P在x轴上移动,三角板的60°角的一边经过C点,另一边与腰AB交与D ,问是否存在最大线段AD长度,如有求出最大值,且此时P点坐标,如没有,要说明理由.