中考数学仿真模拟试题七
一、选择题:(本大题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一项符合题目要求)
1.![]() 的相反数是( )
的相反数是( )
A.-2 B.2 C.![]() D.-
D.-![]()
2.下列运算正确的是( )
A. =±2 B. 2-3=-6 C. x2·x3=x6 D. (-2x)4=16x4
3.如图,给出了过直线外一点作已知直线的平行线的方法,其依据是( )
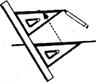 A. 同位角相等,两直线平行
A. 同位角相等,两直线平行
B. 内错角相等,两直线平行
C. 同旁内角互补,两直线平行
D. 两直线平行,同位角相等
 4.下列基本图形中,经过平移、旋转或轴对称变换后,不能得到右图的是 ( )
4.下列基本图形中,经过平移、旋转或轴对称变换后,不能得到右图的是 ( )
![]()
![]() A. B.
A. B.
 | |||
C. D.
5.已知两个分式![]() ,
,![]() .其中x ≠ ±2. 则下面三个结论正确的是( )
.其中x ≠ ±2. 则下面三个结论正确的是( )
A. A=B B. A、B互为倒数 C. A、B互为相反数 D. A大于B
 6.如图是一个正方体的侧面展开图,若将它折成一个正方体,则空白面
6.如图是一个正方体的侧面展开图,若将它折成一个正方体,则空白面
所对的文字应是( )
A.北 B.京
C.欢 D.迎
7.国家统计局发布的统计公报显示:2001到2005年,我国GDP增长率分别为8.3%,9.1%,10.0%,10.1%,9.9%。经济学家评论说:这五年的年度GDP增长率之间相当平稳。从统计学的角度看,“增长率之间相当平稳”说明这组数据的( )较小。
 A. 中位数 B. 标准差 C. 平均数 D. 众数
A. 中位数 B. 标准差 C. 平均数 D. 众数
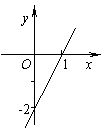
8.已知一次函数y=kx+b的图象如图所示,当x≥0时,y的取值范围
是( )
A. y≥0 B. y≥1 C. -2≤y≤0 D. y≥-2
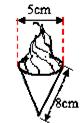 9.如图,冰淇淋蛋筒下部呈圆锥形,则蛋筒圆锥部分包装纸的面积
9.如图,冰淇淋蛋筒下部呈圆锥形,则蛋筒圆锥部分包装纸的面积
(接缝忽略不计)是( )
A.20![]() B.40
B.40![]()
C.20![]()
![]() D.40
D.40![]()
![]()
10.已知二次函数y=2x2+9x+34,当自变量x取两个不同的值x1、x2时,函数值相等,则当自变量x取x1+x2 时的函数值与( )
A.x=1时的函数值相等 B.x=0时的函数值相等
C.x=![]() 时的函数值相等 D.x=-
时的函数值相等 D.x=-![]() 时的函数值相等
时的函数值相等
| 得分 | 评卷人 |
|
|
|
二、填空题(本大题共6小题,每小题3分,共18分,把答案填写在题中横线上)
11. 水位上升用正数表示,水位下降用负数表示,如图,水面从原来的位置到第二次变化后的位置,其变化值是__________.
水位上升用正数表示,水位下降用负数表示,如图,水面从原来的位置到第二次变化后的位置,其变化值是__________.
12.2005年我国国民生产总值为18.23万亿元,国家发
展和改革委员会预计2006年全年国民生产总值将
同比增长10.5%,用科学记数法表示2006年国民生
 产总值为________________亿元(保留三个有效数
产总值为________________亿元(保留三个有效数
字).
13.有四张背面相同的纸牌,其正面分别画有四个
不同的几何图形(如图).小华将这4张纸牌
背面朝上洗匀后摸出一张,则摸出纸牌牌面图
 形为中心对称图形的概率为__________.
形为中心对称图形的概率为__________.
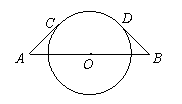
 14.如图,AB=
14.如图,AB=![]() ,O为AB的中点,AC,BD都是半径为3的⊙O的切线,C,D为切点,则弧CD的长为_________.
,O为AB的中点,AC,BD都是半径为3的⊙O的切线,C,D为切点,则弧CD的长为_________.
15.如图,将n个边长都为1cm的正方形按如图所示摆放,点A1、A2、…、An分别是正方形的中心,则n个这样的正方形重叠部分的面积和为___________.
 16.如图,△OAP、△ABQ均是等腰直角三角形,点P、Q
16.如图,△OAP、△ABQ均是等腰直角三角形,点P、Q
在函数![]() 的图象上,直角顶点A、B均在
的图象上,直角顶点A、B均在![]() 轴上,则
轴上,则
点B的坐标为______________.
三、解答题:(本大题共11小题,共72分,解答应写出文字说明和演算步骤)
17.(本小题5分)17.解不等式x>![]() x-2,并将其解集表示在数轴上.
x-2,并将其解集表示在数轴上.
18.(本小题6分)解方程:![]()
19.(本小题6分)八年级三班在召开期末总结表彰会前,班主任安排班长李小波去商店买奖品,下面是李小波与售货员的对话:
李小波:阿姨,您好!
售货员:同学,你好,想买点什么?
李小波:我只有100元,请帮我安排买10支钢笔和15本笔记本.
售货员:好,每支钢笔比每本笔记本贵2元,退你5元,请清点好,再见.
根据这段对话,你能算出钢笔和笔记本的单价各是多少吗?
20.(本小题6分)如图,AB是⊙O的直径,BC是弦,OD⊥BC于E,交于D.
(1)请写出两个不同类型的正确结论;
(2)若BC = 8,ED = 2,求⊙O的半径.
21.(本小题6分)在“不闯红灯,珍惜生命”活动中,文明中学的关欣和李好两位同学某天来到城区中心的十字路口,观察、统计上午7:00~12:00中闯红灯的人次.制作了如下的两个数据统计图.
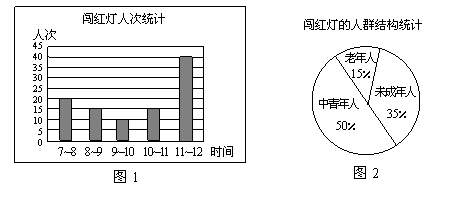
(1)求图1提供的五个数据(各时段闯红灯人次)的众数和平均数.
(2)估计一个月(按30天计算)上午7:00~12:00在该十字路口闯红灯的未成年人约有________人次.
(3)请你根据统计图提供的信息向交通管理部门提出一条合理化建议.
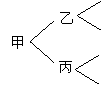
22.(本小题7分)三人之间相互随机传球,由甲开始发球,并作为第一次传球.小明利用树状图对传球次数n与球分别回到甲、乙、丙手中的可能性大小,做了如下的探索:
| 传球次数n | 1 | 2 | 3 | 4 | … |
| 球回到甲手中的概率 | 0 |
|
| … | |
| 球回到乙手中的概率 |
|
| … | ||
| 球回到丙手中的概率 |
|
| … |
(1)请你经历小明的探索过程,帮助小明将上表中的空格填写完整;
(2)根据上表中的数据,请就传球次数![]() 与球分别回到甲、乙、丙手中的可能性大小,提出你的猜想(写出结论即可).
与球分别回到甲、乙、丙手中的可能性大小,提出你的猜想(写出结论即可).
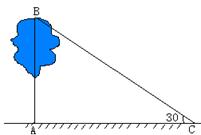
23.(本小题6分)某数学兴趣小组,利用树影测量树高.已测出树AB的影长AC为9米,并测出此时太阳光线与地面成30°夹角.
(1)求出树高AB;(计算结果精确到0.1米,参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
(2)请你再设计一种测量方案,(测量工具有:①皮尺一根;②教学三角板一副;③长为2米的标杆一根;④高度为1.5米的测角仪一架。)写出所需测量工具,并画出测量示意图,标明需要测得数据(角用α、β;线段用a、b、c表示)。
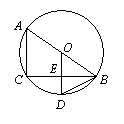
24.(本小题7分)如图,在梯形纸片ABCD中,AD∥BC,AD > CD,将纸片沿过点D的直线折叠,使点C落在AD上的点C′处,折痕DE交BC于点E,连结C’E
(1)求证:四边形CDC’E是菱形;
(2)若BC = CD + AD,试判断四边形ABED的形状,并加以证明.

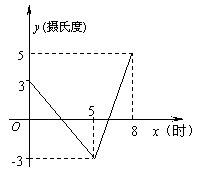
25.(本小题7分)春秋季节,由于冷空气的入侵,地面气温急剧下降到0℃以下的天气称为“霜冻”,由霜冻导致植物生长受到影响或破坏的现象称为霜冻灾害。
某种植物在气温0℃以下持续时间超过3小时,即遭受霜冻灾害,需要采取预防措施。如图是气象台某天发布的该地区气象信息,预报了次日0时至8时气温随时间变化的情况,其中0时至5时,5时至8时的图象分别满足一次函数关系,请你根据图中信息,针对这种植物判断次日是否需要采取防冻措施,并说明理由。
26.(本小题7分)已知在![]() 中,
中,![]() 取一块含
取一块含![]() 角的三角板,将
角的三角板,将![]() 角的顶点放在斜边BC的中点O处,顺时针方向旋转(如图1),使
角的顶点放在斜边BC的中点O处,顺时针方向旋转(如图1),使![]() 角的两边与
角的两边与![]() 的两边AB,AC分别交于E,F(如图2),设BE=x,CF=y.
的两边AB,AC分别交于E,F(如图2),设BE=x,CF=y.
(1)求![]() 与
与![]() 的关系式,并写出
的关系式,并写出![]() 的取值范围;
的取值范围;
(2)三角形绕O点旋转的过程中,△OEF能否成为等腰三角形?若能,求出△OEF是等腰三角形的所有![]() 值。若不能,请说明理由。
值。若不能,请说明理由。
 |
27.(本小题9分)如图1,正方形ABCD的顶点A,B的坐标分别为A(0,10),B(8,4),顶点C,D在第一象限。点P从点A出发,沿正方形按逆时针方向匀速运动,同时,点Q从点E(4,0)出发,沿x轴正方向以相同的速度匀速运动。当点P到达点C时,P,Q两点同时停止运动,设运动的时间为t秒。
(1)求正方形的边长;
(2)当点P在AB边上运动时,△OPQ的面积S(平方单位)与时间t(秒)之间的函数图象为抛物线的一部分(如图2所示),求P,Q两点的运动速度;
(3)求(2)中面积S(平方单位)与时间t(秒)的函数关系式及面积S取最大值时点P的坐标。
(4)若点P,Q保持(2)中的速度不变,则点P沿着AB边运动时,∠OPQ的大小随着时间t的增大而增大;沿着BC边运动时,∠OPQ的大小随着时间t的增大而减小。当点P沿着这两边运动时,使∠OPQ=90°的点P有几个?

中考模拟七答案
一、选择题:1、A 2、D 3、A 4、C 5、C 6、D 7、B 8、D 9、C 10、B
二、填空题:
11. -8 12. 2.01×105 13. ![]() 14.
14. ![]() 15.
15. ![]() 16. (
16. (![]() ,0)
,0)
三、解答题:
17.x>-3 18. x=![]() 19、 钢笔每支5元,笔记本每本3元.
19、 钢笔每支5元,笔记本每本3元.
20.(1)不同类型的正确结论有:
① BE = CE;② = ;③ ∠BED = 90°;④ ∠BOD =∠A;⑤ AC∥OD;
⑥ AC⊥BC;⑦ ![]() ;⑧ S△ABC = BC·OE;⑨ △BOD是等腰三角形;⑩ △BOE ∽ △BAC;等等 (2) ⊙O的半径为5.
;⑧ S△ABC = BC·OE;⑨ △BOD是等腰三角形;⑩ △BOE ∽ △BAC;等等 (2) ⊙O的半径为5.
21.(1)众数为15,平均数为20. (2)1050人次 (3)加强对11-12点时段的交通管理,或加强对中青年人(或未成年人)的交通安全教育.
22.(1)
| 传球次数n | 1 | 2 | 3 | 4 | … |
| 球回到甲手中的概率 | 0 |
|
|
| |
| 球回到乙手中的概率 |
|
|
|
| |
| 球回到乙手中的概率 |
|
|
|
|
(2)猜想:当n为奇数时,P(球回到甲手中)<P(球回到乙手中)=P(球回到丙手中)
当n为偶数时,P(球回到甲手中)>P(球回到乙手中)=P(球回到丙手中)
且第n次传球后球回到甲手中的概率与第n-1次传球后球回到乙或丙手中的概率相等(n>1)。
23.(1)AB=3≈5.2米
(2)可以选:①;③
24.(1) 四边形CDC’E为菱形.
(1) 当BC = CD + AD时,四边形ABED是平行四边形.
25 、解析式为y=![]() x+3 解析式为y=
x+3 解析式为y=![]() x-
x-![]()
次日需要采取防冻措施
26.(1)![]() (1≤x≤2)
(1≤x≤2)
(2)若OE=FE, 则∠OEF=90°,∴![]() =
=![]() ∴x=1
∴x=1
若FE=FO, 则∠EFO=90°,∴![]() ∴x=2
∴x=2
若OE=OF,则![]() ,∴x=
,∴x=![]()
27.(1)AB=10
(2)P,Q两点的运动速度均为每秒1个单位。
(3)![]() ,当t=
,当t=![]() 时,S有最大值 ,点P的坐标为(
时,S有最大值 ,点P的坐标为(![]() ,
,![]() )
)
(4)使∠OPQ=90°的点P有2个.