中考数学复习动点专题
1、 如图,边长为1的正方形OABC的顶点A在x轴正半轴上,将正方形OABC绕点O顺时针旋转30°,使点A落在抛物线![]() (
(![]() )图像上。(1)求抛物线方程。(2)正方形OABC继续顺时针旋转多少度时,点A再次落在抛物线
)图像上。(1)求抛物线方程。(2)正方形OABC继续顺时针旋转多少度时,点A再次落在抛物线![]() 的图像上?并求这个点的坐标。
的图像上?并求这个点的坐标。
 解:(1)设旋转后点A落在抛物线上点A1处,OA1=1,过A1作A1M⊥x轴
解:(1)设旋转后点A落在抛物线上点A1处,OA1=1,过A1作A1M⊥x轴
于M,则OM=![]() ,
,![]() ,
,![]() ,由A1在
,由A1在
![]() 上得
上得![]() ,解得
,解得![]()
∴![]()
(2)由抛物线关于y轴对称,再次旋转后A落在抛物线上的点A2处,点A2与点A1关于y轴对称,易见继续旋转120°,点A2的坐标为![]()
2、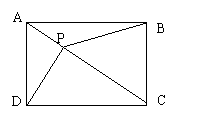 如图,矩形ABCD中,AB=8,BC=6,对角线AC上有一个动点P(不包括A和C),设AP=x,四边形PBCD的面积为y,
如图,矩形ABCD中,AB=8,BC=6,对角线AC上有一个动点P(不包括A和C),设AP=x,四边形PBCD的面积为y,
(1)写出y与x的函数关系,并确定自变量x的范围。
(2)有人提出一个判断“关于动点P,△PBC面积与
△PAD面积之和为常。” 请说明此判断是否正确,并说明理由。
(3)将题目中的矩形改为平行四边形,且已知平行四边形的面积为S,对角线上一动点P,是否有“△PBC面积与△PAD面积之和为常”,并说明理由。
解:(1)过点P作PE⊥BC于点E,在Rt△ABC中,AC=10,PC=AC-AP=10-x,∵PE⊥BC,AB⊥BC,∴△PEC∽△ABC,则![]() ,即
,即![]() ,PE=8-
,PE=8-![]() ,∴△PBC面积=
,∴△PBC面积=![]() ,又△PCD面积=△PBC面积,∴y=
,又△PCD面积=△PBC面积,∴y=![]() (0<x<10)
(0<x<10)
(2)这个判断是正确的,S△PBC+S△PAD=24;(3)有,S△PBC+S△PAD=![]()
 3、如图,平面直角坐标系中,直线AB与x轴,y轴分别交于A(3,0),B(0,
3、如图,平面直角坐标系中,直线AB与x轴,y轴分别交于A(3,0),B(0,![]() )两点,点C为线段AB上的一动点,过点C作CD⊥
)两点,点C为线段AB上的一动点,过点C作CD⊥![]() 轴于点D。
轴于点D。
(1) 写直线AB的解析式;
(2)
若S梯形OBCD=![]() ,求点C的坐标;
,求点C的坐标;
(3) 在第一象限内是否存在点P,使得以P,O,B为顶点
的三角形与△OBA相似。若存在,请求出所有符合条件的点P的坐标;若不存在;请说明理由。
解:(1)直线AB解析式为:y=![]() x+
x+![]()
(2)∵![]() ,
,![]() =
=![]() ,∴
,∴![]()
由OA=![]() OB,得∠BAO=30°,AD=
OB,得∠BAO=30°,AD=![]() CD。
CD。
∴![]() =
=![]() CD×AD=
CD×AD=![]() =
=![]() ,可得CD=
,可得CD=![]() 。
。
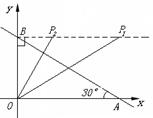 ∴AD=1,OD=2.∴C(2,
∴AD=1,OD=2.∴C(2,![]() )。
)。
(3)当∠OBP=Rt∠时,如图
①若△BOP∽△OBA,则∠BOP=∠BAO=30°,BP=![]() OB=3,
OB=3,
∴![]() (3,
(3,![]() )。
)。
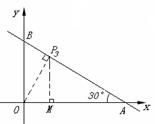 ② 若△BPO∽△OBA,则∠BPO=∠BAO=30°,OP=
② 若△BPO∽△OBA,则∠BPO=∠BAO=30°,OP=![]() OB=1,
OB=1,
∴![]() (1,
(1,![]() )。
)。
当∠OPB=Rt∠时,
③ 过点P作OP⊥BC于点P(如图),此时△PBO∽△OBA,
∠BOP=∠BAO=30°。过点P作PM⊥OA于点M。
 在Rt△PBO中,BP=
在Rt△PBO中,BP=![]() OB=
OB=![]() ,OP=
,OP=![]() BP=
BP=![]() 。
。
∵ 在Rt△PMO中,∠OPM=30°,
∴ OM=![]() OP=
OP=![]() ;PM=
;PM=![]() OM=
OM=![]() .∴
.∴![]() (
(![]() ,
,![]() ).
).
④ 若△POB∽△OBA(如图),则∠OBP=∠BAO=30°,∠POM=30°。
∴PM=![]() OM=
OM=![]() 。∴
。∴![]() (
(![]() ,
,![]() )(由对称性也可得到点
)(由对称性也可得到点![]() 的坐标)。
的坐标)。
当∠OPB=Rt∠时,点P在x轴上,不符合要求。
综合得,符合条件的点有四个,分别是:![]() (3,
(3,![]() ),
),![]() (1,
(1,![]() ),
),![]() (
(![]() ,
,![]() ),
),![]() (
(![]() ,
,![]() )。
)。
4、如图,在直角梯形ABCD中,AD∥BC,∠C=90°,BC=16,CD=12,DA=21。动点P从点D出发,沿射线DA的方向以每秒2个单位长度的速度运动;动点Q从点C出发,在线段CB上以每秒1个单位长度的速度向点B运动。点P,Q分别从点D,C同时出发,当Q运动到点B时,点P随之停止运动。设运动的时间为t(秒)。
(1)设△BPQ的面积为S,求S与t之间的函数关系式;
 (2)当t为何值时,以B,P,Q三点为顶点的三角形是
(2)当t为何值时,以B,P,Q三点为顶点的三角形是
等腰三角形?
(3)当线段PQ与线段AB相交于点O,且2AO=OB时,
求∠BQP的正切值;
(4)是否存在时刻t,使得PQ⊥BD?若存在,求出t的
值;若不存在,请说明理由。
 解:(1)首先0≤t≤16,如图,过点P作PM⊥BC,垂足为M,
解:(1)首先0≤t≤16,如图,过点P作PM⊥BC,垂足为M,
则四边形PDCM为矩形,PM=DC=12。∵QB=16-t,
∴S=12×(16-t)÷2=96-t,0≤t≤16。
(2)设△BPQ是等腰三角形,分三种情况:①PQ=BQ,
在Rt△PMQ中,PQ2=t2+122=BQ2=(16-t)2,解得t=3.5;②BP=BQ,在Rt△PMB中,BP2=(16-2t)2+122=BQ2=(16-t)2,即3t2-32t+144=0,无解。③PB=PQ,由PB2=PQ2,得t2+122=(16-2t)2+122,整理得3t2-64t+256=0,解得![]() (不合题意,舍去)。综上可知,答案为t=3.5或
(不合题意,舍去)。综上可知,答案为t=3.5或![]() 秒。
秒。
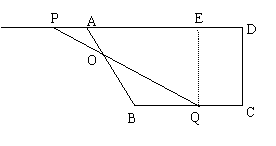 (3)如图,由△OAP∽△OBQ,得
(3)如图,由△OAP∽△OBQ,得![]() .
.
∵AP=2t-21,BQ=16-t, ∴2(2t-21)=16-t, ![]() ,
,
过点Q作QE⊥AD,垂足为E。∵PD=2t,ED=QC=t,
∴PE=t。在Rt△PEQ中,

![]()
(4)设存在时刻t,使得PQ⊥BD,如图,过点Q作QE⊥AD,
垂足为E,易见Rt△BDC∽Rt△QPE, ![]() ,即
,即


![]() ,解得t=9。所以当t=9秒时,PQ⊥BD。
,解得t=9。所以当t=9秒时,PQ⊥BD。
5、如图,在Rt△ABC和Rt△DEF中,
∠ABC=90°,AB=4,BC=6,∠DEF=90°,
DF=EF=4。
(1)移动△DEF,使边DE与AB重合(如图1),再将△DEF沿AB所在的直线向左平移,使点F落在AC上(如图2),求BE的长。
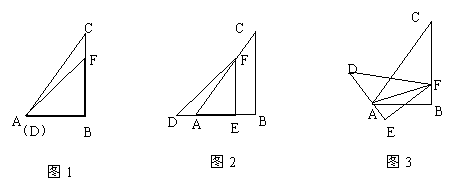
(2)将图2中的△DEF绕点A顺时针旋转,使点F落在BC上,连接AF(如图3),请找出图中的全等三角形,并说明它们全等的理由(不再添加辅助线和标注其它字母)
解:(1)∵EF∥BC ∴∠FEA=∠B=90°,∠CAB=∠FAE。∴△AEF∽△ABC,![]() 。
。
∵AB=4,BC=6,DE=EF=4,∴![]() ,AE=
,AE=![]() ,∴BE=AB-AE=4-
,∴BE=AB-AE=4-![]() =
=![]()
(2)Rt△AEF≌Rt△FBA,在Rt△AEF和Rt△FBA中,EF=BA,AF=FA,∠B=∠E=90°
∴Rt△AEF≌Rt△FBA