三角形四边形综合能力检测题
一、选择题（每小题2分，共28分）
（ ）1．时钟8点整，时针与分针之间的夹角为
A．120° B．100° C．180° D．160°
（ ）2．在△ABC中，∠C=90°，AB=BC，AD是∠BAC的平分线，DE⊥AB垂足为E，若AB=20cm，则△DBE的周长为 A．20cm B．16cm C．24cm D．18cm
（ ）3．一个三角形的两边长分别为3和7，且第三边长为整数，这样的三角形的周长最小值是 A．14 B．15 C．16 D．17
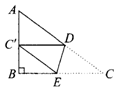
（ ）4．（2006年黑龙江省）如图1，△ABC中，∠B=90°，AB=6，BC=8，将△ABC沿DE折叠，使点C落在AB边上的C′处，并且C′D∥BC，则CD的长是
A．
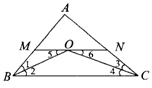
（ ）5．如图2，△ABC中，∠B与∠C的平分线相交于点O，过点O作MN∥BC，分别交AB、AC于点M、N，若AB=12，AC=18，BC=24，则△AMN的周长
A．30 B．36 C．39 D．42
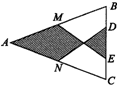
（ ）6．如图3，△DAC和△EBC均是等边三角形，AE、BD分别与CD、CE交于点M、N，有如下结论： ①△ACE≌△DCB；②CM=CN；③AC=DN．其中，正确结论的个数是 A．3个 B．2个 C．1个 D．0个
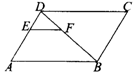
（ ）7．如图4，在平行四边形ABCD中，EF∥AB，DE：AE=2：3，EF=4，则CD的长为
A．
B．8 C．10
D．16
|
|
|
|
（ ）8．若一个正多边形的每一个内角都等于120°，则它是
A．正方形 B．正五边形 C．正六边形 D．正八边形
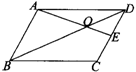
（ ）9．（2006年绍兴市）如图5，在平行四边形ABCD中，E为DC边的中点，AE交BD于点O，若S△DOE=9，则S△AOB等于 A．18 B．27 C．36 D．45
|
|
|
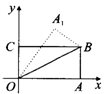
（ ）10．如图6，在直角坐标系中，将矩形OABC沿OB对折，使点A落在点A1处，已知OA=
，AB=1，则点A的坐标是
A．（
，
） B．（，3） C．（，） D．（
，）
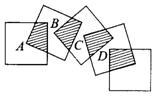
（ ）11．将五个边长都为2的正方形按如图7所示摆放，点A、B、C、D分别为四个正方形中心，则图中四块阴影面积的和为 A．2 B．4 C．6 D．8
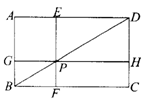
（ ）12．（2006年黑龙江省）如图8，在矩形ABCD中，EF∥AB，GH∥BC，EF、GH的交点P在BD上，图中面积相等的四边形有 A．3对 B．4对 C．5对 D．6对
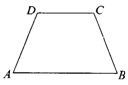
（ ）13．如图9，等腰梯形ABCD中，AB∥DC，AD=BC=8，AB=10，CD=6，则梯形ABCD的面积是 A．16
B．16
C．32
D．16
（ ）14．（2006年黑龙江省）如图10，E、F分别是正方形ABCD的边CD、AD上的点，且CE=DF，AE、BF相交于点O，下列结论①AE=BF；②AE⊥BF；③AO=OE；④S△AOB=S四边形DEOF中，错误的有
A．1个 B．2个 C．3个 D．4个
|
|
|
二、填空题（每小题3分，共36分）
1．已知等腰三角形的腰长是6cm，底边长是8cm，那么以各边中点为顶点的三角形的周长是_______．
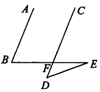
2．如图11，已知AB、CD相交于点O，AO=BO，要判定图中的两个三角形全等，只需再补充一个条件，这个条件可能是___________．
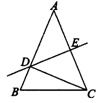
3．如图12，AB∥CD，∠B=68°，∠E=20°，则∠D的度数为______．
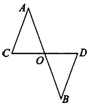
4．如图13，△ABC中，AB=AC，∠A=45°，AC的垂直平分线分别交AB，AC于D，E两点，连接CD．如果AD=1，那么tan∠BCD=________．
5．（2006年盐城市）如图14所示，已知：在△ABC中，∠A=60°，∠B=45°，AB=8，则△ABC的面积是_________（结果可保留根号）
|
|
|
|
|
6．如图15，△ABC中，AB=AC，M、N分别是AB、AC的中点，D、E为BC上的点，连结DN、EM．若AB=13cm，BC=10cm，DE=5cm，则图中阴影部分的面积为______cm2．
7．如图16，在矩形ABCD中，AB=3，AD=4，P是AD上的动点，PE⊥AC于E，PF⊥BD于F，则PE+PF的值为________．
8．如图17，若将四根木条钉成的矩形木框变成平行四边形ABCD的形状，并使其面积为矩形面积的一半，则这个平行四边形的最小内角等于________．
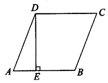
9．如图18，在菱形ABCD中，DE⊥AB于E，DE=6，sinA=
，则菱形ABCD的周长为____．
|
|
|
|
10．已知菱形的周长是52cm，一条对角线长是24cm，则它的面积是_______cm2．
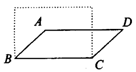
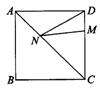11．如图19，正方形ABCD的边长为8，M在DC上，且DM=2，N是安插在AC上的一动点，则DN+MN的最小值为_______．
|
|
三、解答题
1．（7分）已知：如图AB∥ED，点F、点C在AD上，AB=DE，AF=DC．
求证：BC=EF．
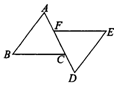
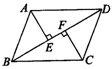
2．（7分）已知：如图，平行四边形 ABCD中，BD是对角线，AE⊥BD于E，CF⊥BD于F，求证：BE=DF．
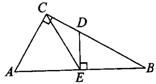
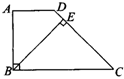3．已知：如图，在梯形ABCD中，AD∥BC，∠ABC=90°，∠C=45°，BE⊥CD于点E，AD=1，CD=2
，求BE的长．
4．（7分）如图，已知：在Rt△ABC中，∠ACB=90°，sinB=
，D是BC上一点，DE⊥AB，垂足为E，CD=DE，AC+CD=9，求BC的长．
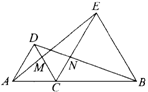
5．（8分）如图，梯形ABCD中，AB∥CD，且AB=2CD，E、F分别是AB、AC的中点，EF与BD相交于点M．
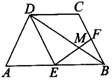（1）求证：△EDM∽△FBM；（2）若DB=9，求BM．
附加题（10分）:
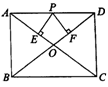
如图， △ ABC 内接于⊙0 , BD 是⊙0 的直径， AE ⊥ BD 于点 E , AE 的延长线交 BC 于点 F ，交⊙0 于 G .
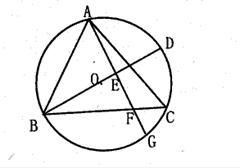( l ）求证：∠ C ＝∠ BAF :
( 2 ）如果 AF = 6 , FG = 2 , CF = 3 ，求 BF 、 AB 的长．