中考试题集锦
（一）填空题
1．（南宁）顺次连接一个任意四边形四边的中点，得到一个_______四边形．
2．（三明）顺次连接对角线相等的四边形的各边中点，所得四边形是_________．
3．（柳州，北海）平行四边形的周长为28，两邻边的比为4：3，则较短的一条边的长为_______．
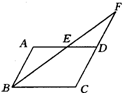
4．（陕西）如图1，已知：在
ABCD中，AB=4cm，AD=7cm，∠ABC的平分线交AD于点E，交CD的延长线于点F，则DF=______cm．
（1） （2） （3）
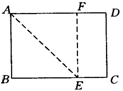
5．（河南）如图2，一张矩形纸片，要折叠出一个最大的正方形，小明把矩形的一个角沿折痕AE翻折上去，使AB与AD边上的AF重合，则四边形ABEF就是一个最大的正方形，他判定方法是_______．
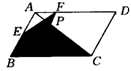
6．（贵阳）如图3，菱形ABCD的对角线的长分别为2和5，P是对角线AC上任一点（点P不与点A、C重合）且PE∥BC交AB于E，PF∥CD交AD于F，则阴影部分的面积是______．
（二）选择题
1．（南宁）如果要用正三角形和正方形两种图案进行密铺，那么至少需要（ ）
A．三个正三角形，两个正方形 B．两个正三角形，三个正方形
C．两个正三角形，两个正方形 D．三个正三角形，三个正方形
2．（宁安）使用同一种规格的下列地砖，不能密铺的是（ ）
A．正六边形地砖 B．正五边形地砖 C．正方形地砖 D．正三角形地砖
3．（山西）下面的选项中，既是轴对称图形又是中心对称图形的是（ ）
A．正六边形 B．平行四边形 C．正五边形 D．等边三角形
4．（常德）已知梯形的上底与下底的比为2：5，且它的中位线长为14cm，则这个梯形的上，下底的长分别为（ ）
A．4cm，10cm B．8cm，20cm C．2cm，5cm D．14cm，28cm
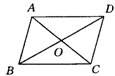
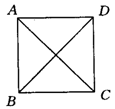
5．（四川）如图4，如果ABCD的对角线AC、BD相交于点O，那么图中的全等三角形共有（ ）
A．1对 B．2对 C．3对 D．4对
（4） （5）
6．（昆明）顺闪连接矩形各边中点所得的四边形是（ ）
A．等腰梯形 B．正方形 C．菱形 D．矩形
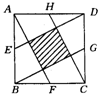
7．（杭州）如图5，E、F、G、H分别是正方形ABCD各边的中点，要使中间阴影部分的小正方形的面积为5，则大正方形的边长应该是（ ）
A．2
B．3 C．5 D．
（三）解答题
1．（南京）如图，已知E、F是ABCD的对角线AC上的两点，AE=CF．
求证：（1）△ABE≌△CDF；（2）BE∥DF。
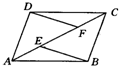
2．（北京海淀）如图，已知在菱形ABCD中，E、F分别是BC、CD上的点，且CE=CF．
（1）求证：△ABE≌△ADF；
（2）过点C作CG∥EA交AF于H，交AD于G，若∠BAE=25°，∠BCD=130°，求∠AHG的度数．
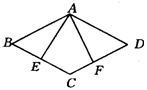
3．（呼和浩特）已知梯形ABCD中，AD∥BC，AD=2，BC=4，对角线AC=5，BD=3，试求此梯形的面积．
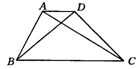
4．（宁夏）将一张矩形纸片沿直线折叠一次，折痕恰好把矩形分为面积相等的两部分．
（1）这样的折痕有多少条？（2）这样的折痕具有什么特点？
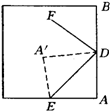
5．（柳州，北海）如图，斜折一页书的一角，使点A落在同一页书内的A′处，DE为折痕，作DF平分∠A′DB，试猜想∠FDE等于多少度，并说明理由．
6．在平面内确定四个点，连结每两点，使任意三点构成等腰三角形（包括等边三角形），且每两点之间的线段长只有两个数值，举例如下（见下图）：相等的线段有：AB=BC=CD=DA，AC=BD，请你画出满足题目条件的三个图形，并指出每个图形中相等的线段．
答案：
一、填空题：
1．平行 2．菱形 3．6 4．3 5．对角线平分内角的矩形是正方形等 6．2．5
二、选择题：
1．A 2．B 3．A 4．B 5．D 6．C 7．C
三、解答题
1．（1）略 （2）证∠BEC=∠DFA．
2．（1）略 （2）100°
3．解：作AE∥DB，交CB延长线于E，作AF⊥BC于F，易知ADBE为平行四边形
∴AE=DB=3 EB=AD=2
∴CE=6 设EF=x 有AE2-EF2=AC2-CF2
即32-x2=52-（6-x）2 x=
∴AF=
=
S梯=
AF（AD+BC）=2．
4．（1）无数条 （2）过矩形对称中心．
5．猜想∠FDE=90°，理由略．毛
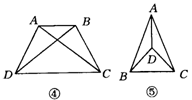
6．【解】
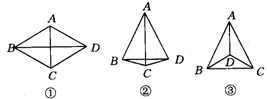
其中：①AB=BC=CD=DA=AC≠BD；
②AB=AC=AD=BD，BC=CD；
③AB=BC=CA，AD=BD=CD；
④AB=AD=BC，AC=BD=DC；
⑤AB=AC，AD=BD=CD=BC．