高中保送生测试数学卷
一选择题:(每题4分,共21分)
1.
|

![]()
 (A)(3,-4)
(B)(-3,-4)(C)(3,4)(D)(-3,4)
(A)(3,-4)
(B)(-3,-4)(C)(3,4)(D)(-3,4)
|
|
|
|
则弧AB的度数是( )
 (A)300 (B)600 (C)900 (D)1200
(A)300 (B)600 (C)900 (D)1200
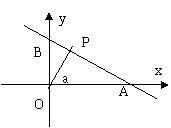
3.如图,已知∠а的终边OP⊥AB,直线AB的方程为
y=![]() x+
x+![]() ,则cosа=( )
,则cosа=( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
 4.银行存款,一年定期年利率为r,取款时还要上交20%的利息税,某人存一年定期x元,到期后所得本金与利息之和为y元,则y与x之间的函数关系为( )
4.银行存款,一年定期年利率为r,取款时还要上交20%的利息税,某人存一年定期x元,到期后所得本金与利息之和为y元,则y与x之间的函数关系为( )
(A)y=(1+ r)x (B)y=(1+ r)×80% x
(C)y=(1+ r×80%)x (D)y=(1+ r×20%)x
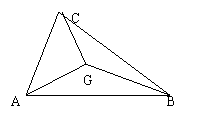
5.G为△ABC的重心,△ABC的三边长满足AB>BC>CA,记
△GAB、△GBC、△GCA的面积分别为S1、S2、S3,则有( )
 (A)S1>S2
>S3 (B)S1 =S2 =S3 (C)S1 < S2 < S3 (D)S1 S2 S3的大小关系不确定。
(A)S1>S2
>S3 (B)S1 =S2 =S3 (C)S1 < S2 < S3 (D)S1 S2 S3的大小关系不确定。
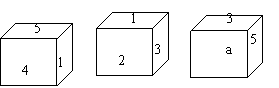
6.如图,一个正方体六个面上分别标有数字
1,2,3,4,5,6.根据图中三种状态,则a
表示的数字是( )
(A)1 (B)2 (C)4 (D)6
7.设b>0,二次函数y=ax2+bx+a2-1的图象为下列之一,则a的值为( )
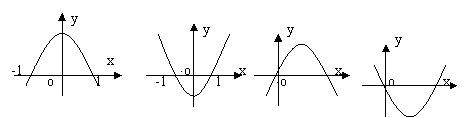
二.填空题:(每小题3分,共21分)
8.已知在直角三角形中,两直角边长分别为1与2。则斜边上的高线长为 。
 9.若x<0且x-
9.若x<0且x-![]() =2
=2![]() ,则x+
,则x+![]() = 。
= 。
10.根据如图的规律,数b= 。
11.规定![]() 表示不超过x的最大整数,如
表示不超过x的最大整数,如
![]() =2,
=2,![]() =-4,若
=-4,若![]() =3,则x的取值范围是 。
=3,则x的取值范围是 。
12.罗马数字有7个基本符号,它们分别是I,V,X,L,C,D,M分别代表1,5,10,50,100,500,1000。罗马数依靠这7个符号变换组合来表示的,如:I,II,III,IV,V,VI,VII,分别表示1,2,3,4,5,6,7;用IX,X,XI,XII,分别表示9,10,11,12;根据以上规律,你认为LII表示的数应该是 。
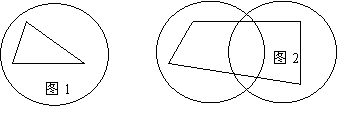 13.对于平面图形A,若存在一个或一个以上的圆,使图形A上任意一点到其中某个圆的圆心的距离都不大于这个圆的半径,则称图形A被这些圆所覆盖,图1中的三角形被一个圆所覆盖,图2中的四边形被两个圆所覆盖,若长宽分别 为2cm与1cm
13.对于平面图形A,若存在一个或一个以上的圆,使图形A上任意一点到其中某个圆的圆心的距离都不大于这个圆的半径,则称图形A被这些圆所覆盖,图1中的三角形被一个圆所覆盖,图2中的四边形被两个圆所覆盖,若长宽分别 为2cm与1cm
的矩形被两个半径均为r的圆覆盖,
则r的最小值为 cm。
14.设坐标平面内有一个质点从
原点出发,沿x轴跳动,每次向正方向
或负方向跳动1个单位,经过5次跳动质点落在点(3,0)(允许重复过此点)处,则质点不同的运动方案共有 种。
三解答题:(第15题10分、其余每题12分,共58分)
15.已知一次函数y1=x+1,点P在反比例函数y2=![]()
![]() (k)0)的图象上,PA⊥x轴,垂足为A,PB⊥y轴垂足为B,且四边形AOBP(O为坐标原点)的面积为2。
(k)0)的图象上,PA⊥x轴,垂足为A,PB⊥y轴垂足为B,且四边形AOBP(O为坐标原点)的面积为2。
(1)求k的值;
(2)求所有满足y1=y2的x;
(3)试根据这两个函数的图象,写出满足y1 > y2 的x的取值范围(只需直接写出结论)
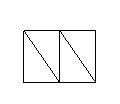 16.如图,把长为2cm的正方形剪成四个全等的直角三角形,
16.如图,把长为2cm的正方形剪成四个全等的直角三角形,
请用这四个直角三角形(全部用上)拼成下列符合要求的图形(互不重叠且没有空隙),并把你的拼法画在下列的方格纸内(方格为1cm×1cm)
(1)画一个不是正方形的菱形 (2)画一个不是正方形的矩形
(3)画一个不是矩形也不是菱形的平行四边形
|
| ||||||
(4)画一个梯形 (5) 画一个不是梯形也不是平行四边形的四边形
|
| ||||||
|
| ||||||
17.上因特网的费用由两部分组成:电话费和上网费。以前某地区上因特网的费用为电话费每分钟0.04元,上网费每分钟0.12元。经调整后,该地区上因特网的费用为电话费每3分钟0.16元,上网费每月不超过60小时,以每小时4元计算,超过6小时部分以每小时8元计算。
(1)根据调整后的规定,将每月上因特网费用y(元)表示为时间x(小时)的函数(每月按30天计算);
(2)某网民经济预算中有一笔每月上网60小时的费用支出(每月按30天计算),调整收费后,若要不超过其经济预算中上网费的支出,该网民现在可上网多少小时(精确到0.01小时)?
 18.一家餐馆要想拥有很多老顾客,菜单的设计就要富有变化,某餐馆的老板提出一份计划,她保证一年当中没有任何两天的菜单会一模一样,她把每天的餐饮分为四大类。包含有:(1)马铃薯等主食类;(2)肉类;(3)蔬菜类;(4)甜点。下面列出各类的细目。
18.一家餐馆要想拥有很多老顾客,菜单的设计就要富有变化,某餐馆的老板提出一份计划,她保证一年当中没有任何两天的菜单会一模一样,她把每天的餐饮分为四大类。包含有:(1)马铃薯等主食类;(2)肉类;(3)蔬菜类;(4)甜点。下面列出各类的细目。
在这一年的第一天,菜单是炸薯片、猪肉、豌豆和苹果派,然后在第二天再换到第二行,当一列内所有项目皆轮过一遍之后,再依序从最上面一项开始轮起。例如某一天的菜单是米饭、鱼肉、豆芽和苹果派,则次日的菜单是炸薯片、牛排、豌豆和冰淇淋。
请问同一种菜式的菜单经多久才会再重复一次?第100天的菜单为何?又哪一天的菜单是烤马铃薯、羊肉、卷心菜和苹果派?
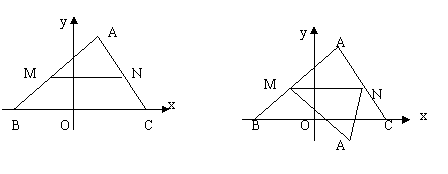
19.如图,点B、C在x轴上(点B在点C的左边),点A在第一象限,过A、B、C三点的抛物线的解析式是y=![]() x2+
x2+![]() 。M是AB边上的一动点(M与点A、B不重合),过M作MN∥BC,交AC与点N,若△ABC的面积是25平方单位,设MN=a
。M是AB边上的一动点(M与点A、B不重合),过M作MN∥BC,交AC与点N,若△ABC的面积是25平方单位,设MN=a
(1)用a表示△AMN的面积;
(2)将△AMN沿MN对折,使△AMN紧贴四边形BCNM(边AM、AN落在四边形BCNM所在平面内),设点A落在平面BCNM内的点为A‘,△A’MN与四边形BCNM重叠部分的面积为S。
①试写出S关于的函数关系式;
②求S的最大值。A