
 高中招生考试数学试卷
高中招生考试数学试卷
一、填空题(每小题4分,共24分)
1.若![]() ,则代数式
,则代数式![]() 的值为_____________.
的值为_____________.
2.在![]() 中,
中,![]() ,现以AB为轴旋转一周得到一个几何体,则该几何体的表面积为_____________.
,现以AB为轴旋转一周得到一个几何体,则该几何体的表面积为_____________.
3.已知圆内接正三角形的边长为![]() ,则同圆外切正三角形的面积为___________.
,则同圆外切正三角形的面积为___________.
4.已知二次函数![]() 的图象与
的图象与![]() 轴交于A、B两点,点C是抛物线上异于A、B的一个点,当
轴交于A、B两点,点C是抛物线上异于A、B的一个点,当![]() 的面积等于__________时,满足条件的点C有且只有三个.
的面积等于__________时,满足条件的点C有且只有三个.
5.对于实数![]() ,定义新运算
,定义新运算![]() ,其中
,其中![]() 为常数,等式右边为通常的加法和乘法运算,若
为常数,等式右边为通常的加法和乘法运算,若![]() ,
,![]() ,则
,则![]() _____________.
_____________.
![]() 6.使用计数器依照预先编制的程序进行计算,当依次输入两个数据为1和1时,输出的结果为2;若依次输入两个数据为
6.使用计数器依照预先编制的程序进行计算,当依次输入两个数据为1和1时,输出的结果为2;若依次输入两个数据为![]() 时,输出的结果为
时,输出的结果为![]() ,依次输入两个数据为
,依次输入两个数据为![]() 时,输出的结果为
时,输出的结果为![]() ,则当依次输入两个数据为
,则当依次输入两个数据为![]() 时,输出的数据结果为_____________.
时,输出的数据结果为_____________.
二、选择题(每小题5分,共30分)
1.已知![]() ,则
,则![]() 化简后为
( )
化简后为
( )
| A. | B. | C. | D. |
2.已知![]() ,
,![]() ,且
,且![]() ,则
,则![]() 的值为( )
的值为( )
| A.2 | B.-2 | C.-1 | D.0 |
3.在一列数1,2,3,4,……,1000中,数字“0”出现的次数一共为( )
| A.182 | B.189 | C.192 | D.194 |
4.如图,![]()
![]() 中,
中,![]() 上一点,
上一点,![]() ,
,![]() ,
,![]() ,则
,则![]() 的长是
( )
的长是
( )
| A. |
|
| C.3 | D. |
5.某商场出售甲、乙两种不同价格的笔记本电脑,其中甲电脑因供不应求,连续两次提价10%,而乙电脑因外观过时而滞销,只得连续两次降价10%,最后甲、乙两种电脑均以9801元售出。若商场同时售出甲、乙电脑各一台与价格不升不降比较,商场的盈利情况是 ( )
| A.前后相同 | B.少赚598元 | C.多赚980.1元 | D.多赚490.05元 |
6.小李骑车上学,开始以正常速度匀速行驶,但行驶途中自行车出现了故障,只好停下来修车。修好后,因怕耽误上课,他比修车前加快了骑车速度继续匀驶。下面是行驶路程![]() 关于时间
关于时间![]() 的函数图象,那么符合小李同学行驶情况的大致图象是
的函数图象,那么符合小李同学行驶情况的大致图象是
|
|
|
|
 | |||||||
 | |||||||
|
|
|
|
|
|
|
|
|
|
|
三、解答题:
1.(10分)关于![]() 的方程
的方程![]() 有实数根
有实数根
⑴ 求![]() 的取值范围;
的取值范围;
⑵ 是否存在实数![]() ,使方程有两个不等实根且它们的倒数和等于0?
,使方程有两个不等实根且它们的倒数和等于0?
若存在,求出![]() 的值,若不存在说明理由。
的值,若不存在说明理由。
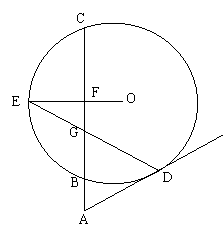

 2.(10分)如图,割线
2.(10分)如图,割线![]() 与⊙
与⊙![]() 相交于
相交于![]() 、
、![]() 两点,
两点,![]() 为⊙
为⊙![]() 上一点,
上一点,![]() 为弧
为弧![]() 的中点,
的中点,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
求证:![]() .
.
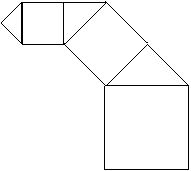
3.(12分)如图所示,在正方形上连接等腰直角三角形和正方形,无限重复同一过程,第一个正方形的边长为1,第一个正方形与第一个等腰直角三角形的面积和为![]() ,第二个正方形与第二个等腰直角三角形的面积和为
,第二个正方形与第二个等腰直角三角形的面积和为![]() ,……,第
,……,第![]() 个正方形与第
个正方形与第![]() 个等腰直角三角形的面积和为
个等腰直角三角形的面积和为![]() .
.
⑴ 求出![]() 、
、![]() 、
、![]() 、
、![]() .
.
⑵ 总结出![]() 与
与![]() 的关系,并猜想出
的关系,并猜想出![]() 与
与![]() 的关系.
的关系.
 |
4.(14分)如图,二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 、
、![]() 两点(
两点(![]() 在
在![]() 的左边),与
的左边),与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,
⑴ 在直线![]() 上有一点
上有一点![]() (
(![]() 在第一象限),使得以
在第一象限),使得以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 、
、![]() 、
、![]() (原点)为顶点的三角相似,求点
(原点)为顶点的三角相似,求点![]() 坐标(用含
坐标(用含![]() 的代数式表示)
的代数式表示)
|
|
|
|
|
|
|
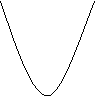
 B.
B.