初三数学中考研究型试题例析
例1：请先阅读材料：解方程
，得
，
，解题的依据是：若两个数的积为零，那么这两个数中至少有一个是零，然后解以下问题：
（1）若两数的积大于零，那么这两数的符号如何？
（2）解不等式：
例2：（02 徐州市）如图，梯子AB斜靠在墙上，∠ACB = 90º，
AB = 5cm，BC = 4cm，当点B下滑到点B/时，点A向左平移
到点A/，设BB/ =
cm
，AA/ =
cm。
（1）用含的代数式表示。
（2）当为何值时，点B下滑的距离与点A向左平移的距离相等？
（3）请你对再取几个值，计算出对应的值，并比较对应的值与值的大小（可以用精确到0.01的近似数表示，也可用无理数表示）。
（4）根据第（1）～（3）题的计算，还可结合图形，观察推测与的大小关系及对应的的取值范围。
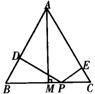
例3：（02 黑龙江）已知等边△ABC和点P，设点P到△ABC三边AB、AC、BC的距离分别为h1，h2，h3，△ABC的高为h。
“若点P在一边BC上（如图1），此时，可得结论：h1 + h2 + h3 = h。”
请直接应用上述信息解决下列问题：
当点P在△ABC内（如图2）、点P在△ABC外（如图3）这两种情况时，上述结论是否成立？若成立，请给予证明；若不成立，h1，h2，h3与h之间又有怎样的关系，请写出你的猜想，不需证明。
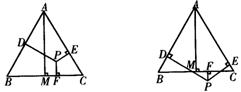
例4：如图，⊙O表示一圆形纸板，根据要求，需通过多次剪裁，把它剪成若干个扇形面积，操作过程如下：第1次剪裁，将圆形纸板等分为4个扇形；第2次剪裁，将上次得到的扇形中的一个再等分为4个扇形；以后按第2次剪裁的作法进行下去。
（1）请你在⊙O中，用尺规作出第2次剪裁后得到的7个扇形（保留痕迹，不写作法）
（2）请你通过操作和猜想，将第3、第4和第n次裁剪后所得扇形的总数（S）填入下表：
| 等分圆及扇形面的次数（n） | 1 | 2 | 3 | 4 | … | n |
| 所得扇形的总个数（S） | 4 | 7 | … |
（3）请你推断，能不能按上述操作过程，将原来的圆形纸板剪成33个扇形？为什么？（02 济南）
练习
1、下面一道题目出自一本数学复习资料：“已知△ABC的面积为S = 18，周长l = 12，求它的内切圆的半径r。”
（1）你会解这道题吗？写出解题过程。
（2）根据你所得到的答案，你认为题目给出的已知条件是否合理？为什么？
2、已知抛物线经过点A（2，0）和B（6，0），最高点C的纵坐标为1。
（1）求抛物线解析式；
（2）设抛物线对称轴交轴于D点，抛物线交轴于E点，请在抛物线上另找一点P，先分别求点A、C、E、P与点D的距离，再求这些点与直线
的距离；
（3）你发现这条抛物线上的点具有何种规律？
3、行驶中的汽车，在刹车后由于惯性的作用，还要继续向前滑行一段距离才能停止，这段距离称为“刹车距离”，为了测定某种型号汽车的刹车性能（车速不超过140千米/时），对这种汽车进行测试，测得的数据如下表：
| 刹车时车速（千米/时） | 0 | 10 | 20 | 30 | 40 | 50 | 60 |
| 刹车距离（米） | 0 | 0.3 | 1.0 | 2.1 | 3.6 | 5.5 | 7.8 |
（1）以车速为轴，以刹车距离为轴，在坐标系中描出这些数据所表示的点，并用光滑的曲线连结这些点，得到函数的大致图象；
（2）观察图象，估计函数的类型，并确定一个满足这些数据的函数的解析式；
（3）该型号汽车在国道上发生了一次交通事故，现场测得刹车距离为46.5米，请推测刹车时的速度是多少？请问在事故发生时，汽车是超速行驶还是正常行驶？