黑龙江省2005年中考数学试题（实验区）
2005年黑龙江省课改实验区初中升学统一考试
〖本卷满分120分，考试时间120分钟〗
一、填空题(每小题3分，满分36分)
1. 中国的互联网上网用户数居世界第二位，用户已超过7800万，用科学记数法表示7800万这个数据为 _________ 万.
2. 函数 
中，自变量x的取值范围是
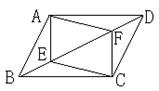3.
如图, E、F是
□ABCD对角线BD上的两
点，请你添加一个适当
的条件: ___________ ，
使四边形AECF是平行四边形.
4． 已知∠α与∠β互余，且∠a=400，则∠β的补角为 _________ 度．
5． 已知抛物线 y=ax2+bx+c 经过点(1，2)与
(-l，4)，则a+c的值是
6. 如图，有6张牌，从中任意抽取两张，点数和是奇数的概率是 ________
7. 有6个数，它们的平均数是12，再添加一个数5，则这7个数的平均数是
8.
小华的妈妈为爸爸买了一件衣服和一条裤子，共用306元. 其中衣服按标价打七折，裤子按标价打八折，衣服的标价为300元，则裤子的标价为 ________ 元.
9. 如图，AB是半圆的
直径，O是圆心，C是
半圆上一点, E是弧AC
的中点，OE交弦AC于D. 若AC=8cm，DE=2cm，则OD的长为 _________ cm
10. 在同一平面内，△ABC与△A1B1C1关于直线m对称, △A1B1C1与△A2B2C2关于直线n对称， 且有m∥n, 则△ABC可以通过一次 ________ 变换直接得到△A2B2C2
11. 已知菱形ABCD的边长为6，∠A=60°，如果点P是菱形内一点，且PB=PD=
，那么AP的长为
_________
12. 一次函数y=kx+3的图像与坐标轴的两个交点之间的距离为5，则k的值为 ________
二、单项选择题(每小题3分，满分24分)
13. 李刚同学设计了四种正多边形的瓷砖图案，在这四种瓷砖中，用一种瓷砖可以密铺平面的是
①
② ③
④
( )
A. ①②④ B. ②③④
C. ①③④ D. ①②③
14. 若梯形的上底长为4，中位线长为6，则此梯形的下底长为
A.5 B.8 C.12 D.16
15. 在下面图形中， 每个大正方形网格都是由边长为1的小正方形组成，则图中阴影部分面积最大的是 ( )
A.
B.
C.
D.
16. 在平面直角坐标系中，点P(-2，3)关于x轴的对称点在 （ ）
A. 第一象限 B. 第二象限
C. 第三象限 D. 第四象限
17. 如图①是一个正方形毛坯， 将其沿一组对面的对角线切去一半，得到一个工件如图②，对于这个工件，左视图、俯视图正确的一组的是
( )
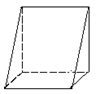
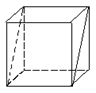① ②
 | |||
 |
a b c d
A.a、b B.b、d C.a、c D.a、d
18. 在相同时刻的物高与影长成比例，小明的身高为1.5米，在地面上的影长为2米，同时一古塔在地面上的影长为40米，则古塔高为( )
A. 60米 B. 40米
C. 30米 D. 25米
19. 不等式组
的解集是 ( )
A. x≤3 B. 1<x≤3
C. x≥3 D. x>1
20. 甲、乙、丙、丁四名运动员参加4×100米接力赛，甲必须为第一接力棒或第四接力棒的运动员，那么这四名运动员在比赛过程中的接棒顺序有 ( )
A.3种 B.4种 C.6种 D.12种
三、解答题(满分60分)
21．(本题5分)
先化简，再求值：
，其中
22．(本题6分)
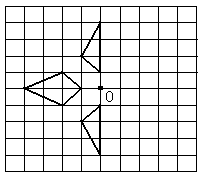
如图网格中有一个四边形和两个三角形.
(1) 请你画出三个图形关于点O的中心对称图形;
(2) 将(1)中画出的图形与原图形看成一个整体图形，请写出这个整体图形对称轴的条数; 这个整体图形至少旋转多少度与自身重合
23．(本题6分)
王叔叔家有一块等腰三角形的菜地， 腰长为40米，一条笔直的水渠从菜地穿过，这条水渠恰好垂直平分等腰三角形的一腰，水渠穿过菜地部分的长为15米(水渠的宽不计)， 请你计算这块等腰三角形菜地的面积．
24．(本题7分)
为了了解业余射击队队员的射击成绩，对某次射击比赛中每一名队员的平均成绩(单位：环，环数为整数)进行了统计．分别绘制了如下统计表和频率分布直方图，请你根据统计表和频率分布直方图回答下列问题：
| 平均成绩 | 0 | l | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 人数 | O | 1 | 3 | 3 | 4 | 6 | 1 | 0 |
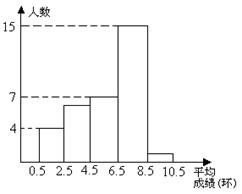
(1) 参加这次射击比赛的队员有多少名?
(2) 这次射击比赛平均成绩的中位数落在频率分布直方图的哪个小组内?
(3) 这次射击比赛平均成绩的众数落在频率分布直方图的哪个小组内?
25．(本题8分)
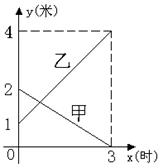
某企业有甲、乙两个长方体的蓄水池，将甲池中的水以每小时6立方米的速度注入乙池，甲、乙两个蓄水池中水的深度y(米)与注水时间x(时)之间的函数图象如图所示，结合图象回答下列问题：
(1) 分别求出甲、乙两个蓄水池中水的深度y与注水时间x之间的函数关系式；
(2) 求注水多长时间甲、乙两个蓄水池水的深度相同；
(3) 求注水多长时间甲、乙两个蓄水池的蓄水量相同．
 |
26．(本题8分)
已知矩形ABCD和点P，当点P在图1中的位置时，则有结论：S△PBC=S△PAC+S△PCD理由：过点P作EF垂直BC，分别交AD、BC于E、F两点．
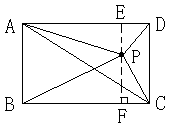
图l
∵ S△PBC+S△PAD=
BC·PF+AD·PE
=BC（PF+PE）=BC·EF=S矩形ABCD
又∵ S△PAC+S△PCD+S△PAD=S矩形ABCD
∴ S△PBC+S△PAD= S△PAC+S△PCD+S△PAD．
∴ S△PBC=S△PAC+S△PCD．
请你参考上述信息，当点P分别在图2、图3中的位置时，S△PBC、S△PAC、SPCD又有怎样的数量关系? 请写出你对上述两种情况的猜想，并选择其中一种情况的猜想给予证明．
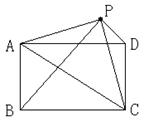
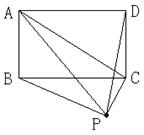
图2 图3
27．(本题10分)
某房地产开发公司计划建A、B两种户型的住房共80套，该公司所筹资金不少于2090万元，但不超过2096万元，且所筹资金全部用于建房，两种户型的建房成本和售价如下表：
| A | B | |
| 成本(万元/套) | 25 | 28 |
| 售价(万元/套) | 30 | 34 |
(1) 该公司对这两种户型住房有哪几种建房方案?
(2) 该公司如何建房获得利润最大?
(3) 根据市场调查，每套B型住房的售价不会改变，每套A型住房的售价将会提高a万元(a>0)，且所建的两种住房可全部售出，该公司又将如何建房获得利润最大?
注：利润=售价-成本
28．(本题10分)
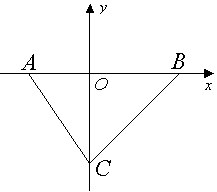
如图，在平面直角坐标系中，Rt△ABC的斜边AB在x轴上，AB=25，顶点C在y轴的负半轴
上，
，点P在线段OC上，且PO、PC
的长(PO<PC)是关于x的方程x2-(2k+4)x+8k=O的两根．
(1) 求AC、BC的长；
(2) 求P点坐标；
(3) 在x轴上是否存在点Q，使以点A、C、P、Q为顶点的四边形是梯形? 若存在，请直接写出直线PQ的解析式；若不存在，请说明理由．
 |