初三学业考试模拟考数学试卷

初三学业考试模拟考数学试卷

（满分150分，考试时间100分钟　）　　　　　　

题号	一	二	三	四	总分
得分

考生注意：

1．本卷含四大题，共25题；

2．除第一、二大题外，其余各题如无特别说明，都必须写出证明或计算的主要步骤．

一．填空题：(本大题共12小题，满分36分）

【只要求直接写出结果，每空格填对得3分，否则得零分】

1．－的相反数是　　　　   ；

2．2x³·（－x²）＝____________；

3．不等式≤0的解是______________；

4．在实数范围内因式分解：_____________________；

5．若方程，设则原方程可化为　　　　　　　 ；

6．函数的自变量x的取值范围是____________________；

7．已知、是一元二次方程2x+4x﹣1=0的两个实数根，那么+=________；

8．已知：在直角三角形ABC中，　AC=4　，那么AB=　　　　；

9．在平面直角坐标系内，O为原点，点P是函数图象上一点，作PG⊥y轴，垂足为G，那么三角形OPG的面积等于　　　　　　　  ;

10．正六边形绕着它的中心最少旋转　　　　　　 度后与它本身重合；

11．相交两圆的半径分别为5和4，公共弦长为6，求两圆的圆心距长 　　　 　　　 ；

12．有一块矩形的纸片ABCD，AB=9,AD=6,将纸片折叠，使得AD边落在AB边上，折痕为AE，再将△AED沿DE向右翻折，AE与BC的交点为F，则△CEF的面积为　　　　　　　　   ．

A　　　　　　　 　B　  A　　　　　 D　　 B　　D　　B　　

F　　　　　　　

D　　　　　　　　 　C　　　　　 　 E　　　C　 E　　　C

二．选择题：（本题共4小题，满分16分）

【下列各题的四个结论中，有且只有一个结论是正确的，把正确结论的代号写在题后的圆括号内，选对得4分；不选、错选或者多选得零分】

13．下列二次根式中，与是同类二次根式的是　　　　　　　　　　 （　　 ）

（A）；　　　（B）；　　 （C）；　　 （D）．

14．已知一次函数，当时，函数图像一定不经过　  （　　 ）

（A）第一象限； （B）第二象限；（C）第三象限； （D）第四象限．

15．地球的质量为6×10¹³亿吨，太阳的质量是地球质量的3.3×10⁵倍，太阳的质量用科学记数法表示为　　　　　　　　　　　　 　　　　　　　　 （　　）

　　　　（A）1.98×10¹⁸亿吨　　　　　　　　　　　　（B）1.98×10¹⁹亿吨

　　　　（C）1.98×10²⁰亿吨　　　　　　　　　　　　（D）1.98×10⁶⁵亿吨

16．下列语句中，正确的是　　　　　　　　　　　　　  　　　　　　 （　　）

 （A）三个点确定一个圆；　　　 （B）一个圆中可以有无数条弦，但只有一条直径；

（C）弦相等则所对的弧相等； 　（D）圆是轴对称图形，又是中心对称图形．

三．（本题共5小题，满分48分）

17．（本题满分9分）

计算：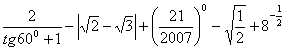

18．（本题满分9分）

解方程组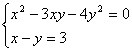

解：

19．（本题满分10分，每小题满分各5分）

如图，在中，，AC=BC，AD平分，，垂足为E．

　 （1）求证：；

　 （2）若AB=10，求BD的长度．

（1）证明：　　　　　　　　　　　　　　　　　　　　　　　　 

C

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D

 

A　　　　  　　 E　　 B

（2）解：

20．（本题满分10分）

某中学举行了一次演讲比赛，分段统计参赛同学的成绩，结果如下表：（分数均为整数，满分为100分，表中分数段包含端点分数）

分数段（分）	61～70	71～80	81～90	91～100
人  数（人）	2	8	6	4

请根据表中提供的信息，解答下列各题：

（1）参加这次演讲比赛的同学有　　　　  人；

（2）已知成绩在91～100分的同学为优胜者，那么优胜率为　　　　  ；

（3）所有参赛同学的平均得分M（分）在什么范围内？

　　 答：　　　　　　　　　　　　　　　　  ．

（4）将成绩频率分布直方图补充完整．

21．（本题满分10分）

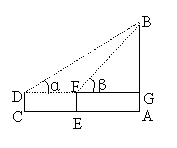
如图，在C处用高1.20米的测角仪测得塔AB顶端B的仰角α=30°，向塔的方向前进20米到E处，又测得塔顶端B的仰角β=45°．求塔AB的高（这里，结果精确到百分位）．

 

 

 

四．（本题共4小题，满分50分）

22．（本题满分12分，每小题满分4分）

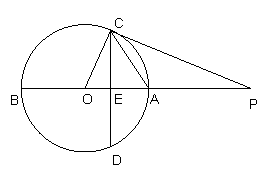
如图，AB是⊙O的直径，点P在BA的延长线上，弦CD⊥AB于点E，

OE：EA＝1：2，PA＝6，∠POC＝∠PCE．

（1）　  求证：PC是⊙O的切线；

（2）　  求⊙O的半径；

（3）　  求sin∠PCA的值．

　

23．（本题满分12分）

在男子引体向上团体比赛中，按每个组的人数不超过10个人为原则分组．比赛结果是：甲组男生共完成了36次，乙组共有5名男生，他们共完成了41次；又知甲、乙两组男生人均完成的次数比甲组男生人均完成的次数多1次．问甲组共有男生多少名？

24．（本题满分12分，每小题满分4分）

已知一条抛物线的对称轴是直线x=1；它与x轴相交于A，B两点（点A在点B的左边），

且线段AB的长是4；它还与过点C（1，-2）的直线有一个交点是D（2，-3）．

　（1）求这条直线的函数解析式；

　（2）求这条抛物线的函数解析式；

　（3）若这条直线上有P点，使，求点P的坐标．

25．（本题满分14分，第（1）小题满分2分，第（2）小题满分5分，第（3）小题满分4分，第（4）小题满分3分）

如图，在平面直角坐标系中，△ABC的顶点A在原点，边AC在x轴的正半轴，AC＝16，∠BAC＝60°，AB＝10，⊙P分别与边AB、AC相切于D、E(切点D、E不在边AB、AC的端点)，ED的延长线与CB的延长线相交于点F.

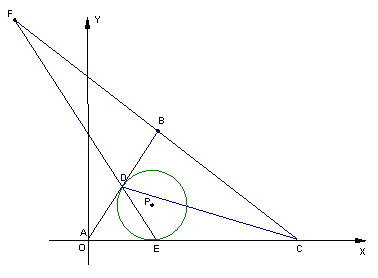
（1）求BC边的长和△ABC的面积；

（2）设AE＝x，DF＝y，写出y与x的函数解析式，并写出自变量x的取值范围；

（3）探索△ADC与△DBF能否相似？若能相似，请求出x的值，同时判断此时⊙P与边BC的位置关系，并证明之；若不能相似，请说明理由；

（4）当⊙P与△ABC内切时，⊙P与边BC相切于G点，请写出切点D、E、G的坐标(不必写出计算过程).