初中毕业升学考试数学科试题
（含超量题满分110分，考试时间100分钟）
特别提醒：
1.选择题用2B铅笔填涂其余答案一律用黑色笔填写在答题卡上，写在试题卷上无效.
2.答题前请认真阅读试题及有关说明.
3.请合理安排好答题时间.
一、选择题（本大题满分20分，每小题2分）
在下列各题的四个备选答案中，只有一个是正确的，请在答题卡上把你认为正确的答案的字母代号按要求用2B铅笔涂黑.
1．
的相反数是
A.
B.
C.
D.
2.参加2007年海南省初中毕业升学考试的学生达到113000人，用科学记数法表示这个人数应记作
A.
B.
C.
D.
|
A.
B.
C.
D.
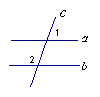
4.如图1，两条直线
、
被第三条直线
所截，如果∥，
，那么
的度数为
A.
B.
C.
D.
图1
|
所示，则这个立体图形应是下图中的
图
A
B
C
D
6.一次函数
的图象不经过
A.第一象限 B. 第二象限 C. 第三象限 D. 第四象限
7.在Rt
中，
，如果
，
，那么
的值是
A.
B.
C.
D.
8.如图
，已知
，那么添加下列一个条件后，仍无法判定∽
的是
|
B.
C.
D.
图
图4
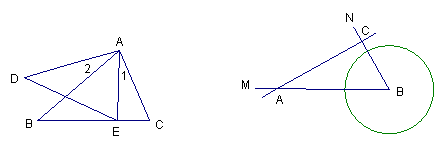
9.如图4，⊙
的半径为4
，
，点
、
分别是射线
、
上的动点，且直线
.当
平移到与⊙相切时，
的长度是
A.
B.
C.
D.
10.自然数
、
、、
、
从小到大排列后，其中位数为，如果这组数据唯一的众数是,那么，所有满足条件的、中，
的最大值是
A. B. C.
D.
二、填空题（本大题满分24分，每小题3分）
11.分解因式：
= .
12.反比例函数
的图象经过点
，则这个反比例函数的关系式为 .
13.函数
的自变量的取值范围是 .
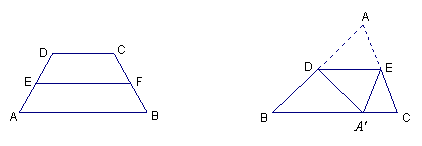
14.如图，已知等腰梯形
的中位线
的长为，腰
的长为，则这个等腰梯形的周长为 .
|
图 图
15.如图，沿
折叠后，点落在
边上的
处，若点
为边的中点，
，则
的度数为 .
16.已知关于的方程
的一个根是
，那么
.
|
个白球，
个黄球，它们除颜色不同外，其余均相同.若从中随机摸出一个球，它是黄球的概率是
，则= .
18.已知一个圆柱体侧面展开图为矩形（如图7），
若
，
，则该圆柱体的体积约
为 
（取
，结果精确到0.1）.
图7
三、解答题（本大题满分66分）)
19. （本题满分10分，每小题5分）
（1）计算：
|
|
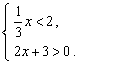
20. （本题满分10分）“海之南”水果种植场今年收获的“妃子笑”和“无核Ⅰ号”两种荔枝共
千克，全部售出后收入
元.已知“妃子笑”荔枝每千克售价
元，“无核Ⅰ号”荔枝每千克售价
元，问该种植场今年这两种荔枝各收获多少千克？
|
）与“海南省
年教育经费支出扇形统计图”（图
）提供的信息，回答下列问题：
图
图
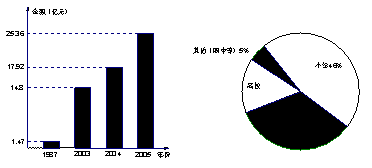
（1）海南省年中学教育经费支出的金额是 亿元（精确到0.01）；
（2）海南省年高校教育经费支出占全年教育经费总支出的百分率是 ,在图
中表示此项支出的扇形的圆心角的度数为 ；
（3）海南省年教育经费总支出与
年比较，增长率是 （精确到0.01%），相当于建省前的
年的 倍（精确到个位）；
（4）请根据以上信息，写出一条你认为正确的结论或对海南教育发展有益的建议.
|
的方格纸中，的顶点坐标分别为
、
和
.
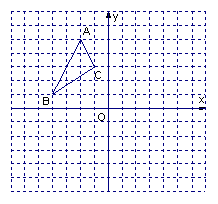
（1）作出关于轴对称的
，并写出
点、、的对称点
、
、
的坐标；
（2）作出关于原点
对称的
，并写
出点、、的对称点
、
、
的坐标；
（3）试判断：与是否关于轴对称（只需写出判断结果）.
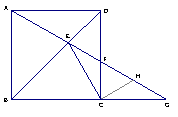
23.（本题满分12分）如图11，在正方形中，点
在
边上，射线
交
于点
，交的延长线于点
.
（1）求证：≌
；
（2）过点作
，交
于点
，求证：
；
|
，
，试问是否存在的值，使
为等腰三角形，若存在，请求出的值；若不存在，请说明理由.
|
图11
图
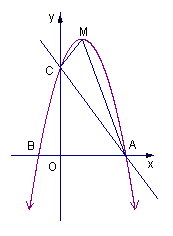
24. （本题满分14分）如图，直线
与轴交于点，与轴交于点，已知二次函数的图象经过点、和点
.
（1）求该二次函数的关系式；
（2）设该二次函数的图象的顶点为
，求四边形
的面积；
（3）有两动点、同时从点出发，其中点以每秒
个单位长度的速度沿折线
按→→的路线运动，点以每秒个单位长度的速度沿折线
按→→的路线运动，当、两点相遇时，它们都停止运动.设、同时从点出发
秒时，
的面积为S .
①请问、两点在运动过程中，是否存在∥
，若存在，请求出此时的值；若不存在，请说明理由；
②请求出S关于的函数关系式，并写出自变量的取值范围；
③设
是②中函数S的最大值，那么 = .