初中毕业生数学模拟试卷（一）

初中毕业生数学模拟试卷（一）

一，选择题：

1．我国首次载人航天飞船“神州五号”成功绕地球飞行14圈，行程约591000千米，用科学计数法表示正确的是（　　）

A;591×10³千米　 B;5.91×10³千米　　 C; 5.91×10⁵千米　　　 D;0.591×10⁶千米

2．若∠A是锐角，sinA=cosA,则∠A的度数是（　　）

A;30⁰　　　　　  B;45⁰　　　　　　　 C;60⁰　　　　　　　　 D;90⁰

3．到△ABC的三个顶点距离相等的点是△ABC的（　　）

A;三条中线的交点　　　　　　　　  B;三条高线的交点　

C;三条角平分线的交点　　　　　　  D;三条边的垂直平分线的交点。

4．四边形ABCD是圆内接四边形，若∠A:∠B:∠C=1:2:3，则∠D等于(　　)

A;60⁰ 　　　　　 B;90⁰　　　　　　  C;100⁰　　　　　　　  D;120⁰

5.点P关于x轴对称的点在双曲线y=上，则k的值为（　　）

A;2　　　　　　  B;－2　　　　　　 C;　　　　　　　　 D;－

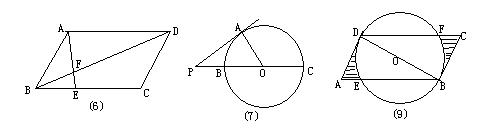
6.如图，在平行四边形ABCD中，E是BC上一点，BE:EC=2:3,AE交BD于F，则BF:FD等于(　 )

A;2；3　　　　  B;2：5　　　　　　 C;3：5　　　　　　　  D;5：7

7．如图，PA切⊙O于点A，PBC是⊙O的割线且过O点，PA=4,PB=2,则⊙O的半径等于（　　）

A;3　　　　　　 B;4　　　　　　　  C;5　　　　　　　　　 D;6

8.关于x的方程ax²+2x+1=0有两个不相等的实根，则a的取值范围是（　　）

A;a>1　　　　　 B;a=1　　　　　　  C;a<1　　　　　　　　 D;a<0或0<a<1

9.如图，在平行四边形ABCD中，BD⊥AD,以BD为直径作⊙O,交AB于E，交CD于F，若BD=12，AD:AB=1:2,则图中阴影部分的面积为(　　 )

A;　　　　 B;15　　  C;30　　　　  D;48

10.已知抛物线y=x²+(m+1)x－m²－1（m为整数），与x轴交于点A，与y轴交于点B，且OA=OB，则m的值为（　　）

A;　　　 B;　　　　　  C;－2　　　　　　　　 D; 或－2

二，填空题：

11．分解因式：a³－6a²+9a－ab²=　　　　　　　　　　 .

12.某商品的标价是1100元，打8折出售，仍可获利10％，则此商品的进价为　　　 元。

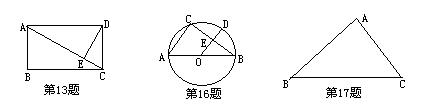
13．如图，在矩形ABCD中，DE⊥AC于E，设∠ADE=,且cos=,ab=4,则AD的长为　　　。

14．如果圆柱底面直径为6cm,母线长为4cm,那么圆柱的侧面积为　　　　　　　 。

15．九年级某次调研考试中，统计甲乙两班的数学考试成绩（单位：分）的情况如下表：

班级	考试人数	平均分	中位数	众数	方差
甲	57	72	60	68	210
乙	57	70	65	68	102

则下列判断：①甲班学生的成绩及格率高于乙班学生的成绩及格率。

②甲班学生的成绩平均分高于乙班学生的成绩平均分。 ③甲班学生的成绩波动高于乙班学生的成绩的波动。④将两班学生的成绩分别从高到低的顺序排列，则处在中间位置的成绩都是68分。

其中正确的是　　　　　　 。（把所有正确判断的序号都填上）

16．如图，AB是⊙O的直径，OA=5cm, D是弧BC的中点，OD交BC于E，DE=2cm,则AC的长为

　　　　　 。

17．如图，在△ABC中，AB=, AC=2, BC=,则∠A的度数是　　　　  .

18.⊙O₁和⊙O₂的半径分别为2cm和4cm,当圆心距在　　　　　 范围内变化时，两圆无公共点

三，解答题：

19.计算

20．解方程：

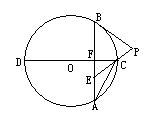
21．如图，AB是⊙O的直径，P是AB的延长线上的一点，PC切⊙O于点C，⊙O的半径为3，∠PCB=30⁰

（1）求∠ABC的度数　　　（2）求PC的长。

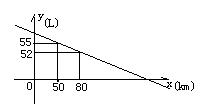
22.某种汽油箱可储油60升，加满油并开始行驶，油箱中的剩油量y（升）与行驶的里程x（千米）之间的函数关系为一次函数，如图：

（1）求y与x的关系式。　　（2）加满一箱油汽车可行驶多少千米？

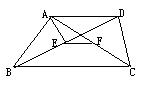
23.在梯形ABCD中，AD∥BC,E和F分别为BD和AC的中点，BD平分∠ABC

求证：（1）AE⊥BD　　 （2）EF=

24.甲乙两车从A,B两地同时相向匀速而行，相遇后甲车4小时到达B地，乙车9小时到达A地，甲乙两车走完全程各用几小时？

25.如图，⊙O的弦AB垂直于直径CD，垂足为F，点E在AB上，且EA=EC

（1）　　　 求证：AC2=AE·AB

（2）　　　 延长EC到点P，连结PB，若PB=PE，试判断PB与⊙O的位置关系，并说明理由。

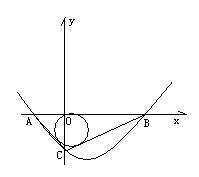
26.如图，在Rt△ABC中，∠ACB=90⁰ (∠CAB>∠CBA),它的两个锐角的正弦值恰好为方程4x²－2(m+1)x+m=0的两个根，它的内切圆半径为，抛物线y=ax²+bx+c过A,B,C三点

（1）　　　 求m的值

（2）　　　 求这个抛物线的解析式

（3）　　　 在抛物线上是否存在点P，使S_△ABP=8，若存在，请求出P点的坐标；若不存在，请说明理由。

参考答案：1. C　　2.B　　3.D　　4.B　　5.A　  6.B　　7.A　　 8.D　　9.C　　 10.C

11.a(a+b－3)(a－b－3)　　12.800　　13.　  14.24cm²　　15.②③　　16.6cm　　17.75⁰

18.小于2cm或大于6cm　　　 19.2　　　 20.x=－3　　　　21. 60⁰,　3　　  22. (1)y=　(2)600千米　　　23。略　　　24。10小时，15小时　　25。（1）略

（2）PB为⊙O的切线　　 26.(1)m=　(2)y=　 (3)存在点（－3，），（5，）