课改实验区缙云县中考模拟试卷2006、5.
命题人:沈崇明
说明:
本试卷分卷Ⅰ和卷Ⅱ两部分;卷Ⅰ为选择题,卷Ⅱ为非选择题.
本试卷满分为150分,考试时间为120分钟.
卷Ⅰ(选择题,共40分)
 |
一、选择题(本大题共10个小题;每小题4分,共40分.在每小题给出的四个选项中,只
有一项是符合题目要求的)
1. ![]() 的值是
的值是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2. 据统计,2005“超级女声”短信投票的总票数约张,将这个数写成科学计数法是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3. 下列计算中,正确的是
A.2a+3b=5ab B.a·a3=a3
C.a6÷a2=a3 D.(-ab)2=a2b2
4. 如图所示的几何体,它的主视图是 ( )

(第4题) A. B. C. D.
5. 已知一组数据5,15,75,45,25,75,45,35,45,35,那么40时这一组数据的
A.平均数但不是中位数 B.平均数也是中位数
C.众数 D. 中位数但不是平均数
6. 下列美丽的图案,既是轴对称图形又是中心对称图形的个数是
 |
(A)1个 (B)2个 (C)3个 (D)4个
7. 下列事件中:确定事件是 ( )
A、掷一枚六个面分别标有1~6的数字的均匀骰子,骰子停止转动后偶数点朝上
B、从一副扑克牌中任意抽出一张牌,花色是红桃
C、任意选择电视的某一频道,正在播放动画片
D、在同一年出生的367名学生中,至少有两人的生日是同一天。
8. 中央电视台“开心辞典”栏目曾有这么一道题:圆的半径增加了一倍,那么圆的面积增加了 ( )
A 1倍 B 2倍 C 3倍 D 4倍
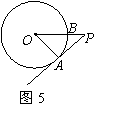 9.如图5,PA为⊙O的切线,A为切点,PO交⊙O于点B,PA=4,
9.如图5,PA为⊙O的切线,A为切点,PO交⊙O于点B,PA=4,
OA=3,则cos∠APO的值为
A.![]() B.
B.![]()
C.![]() D.
D.![]()
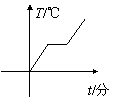
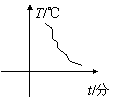
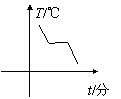
10. 蜡是非晶体,在加热过程中先要变软,然后逐渐变稀,然后全部变为液态,整个过程温度不断上升,没有一定的熔化温度,如图所示,四个图象中表示蜡溶化的是
 |  | ||||||
 | |||||||
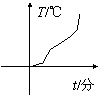 | |||||||
(A) (B) (C) (D)
卷Ⅱ(非选择题,共110分)
 |
二、填空题(本大题共6个小题;每小题5分,共30分.把答案写在题中横线上)
11. 点A(—2,1)在第_______象限.
 |
12. 函数![]() 的自变量
的自变量![]() 的取值范围是_____________.
的取值范围是_____________.
13.二次函数y=x2—2x+1的对称轴方程是x=_______.
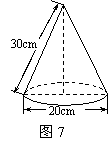
14.图7是小明制作的一个圆锥形纸帽的示意图.围成这个纸帽
的纸的面积为 cm2(π取3.14).
15. 矩形ABCD中,M是BC边上且与B、C不重合的点,点P是射线AM上的点,若以A、P、D为顶点的三角形与△ABM相似,则这样的点有 个.
16. 自然数中有许多奇妙而有趣的现象,很多秘密等待着我们去探索!比如:对任意一个自然数,先将其各位数字求和,再将其和乘以 3后加上1,多次重复这种操作运算,运算结果最终会得到一个固定不变的数R,它会掉入一个数字“陷井”,永远也别想逃出来,没有一个自然数能逃出它的“魔掌”.那么最终掉入“陷井”的这个固定不变的数R= .
 三、解答题(本大题共10个小题;共80分)
三、解答题(本大题共10个小题;共80分)
17. 计算(本题满分8分)
(1) ![]()
(2) 解方程:x2+2x-3=0
18. (本小题满分8分)
如图,平行四边形ABCD中,AE⊥BD,CF⊥BD,垂足分别为E、F。
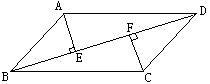 (1)写出图中每一对你认为全等的三角形;
(1)写出图中每一对你认为全等的三角形;
(2)选择(1)中的任意一对进行证明。
19. (本小题满分8分)
我市防疫部门为了防止非典型性肺炎的传播,计划对库存的过氧乙酸消毒液进行优惠酬宾销售,得到了广大市民的热烈欢迎。制定出这样两种销售方案:①若购买100公斤以上,多出的部分给予8折的优惠。②直接进行9折销售。已知这种消毒液的单价为3元/公斤。请你根据购买者的用量讨论一下如何购买比较划算?
20. (本小题满分8分)
在△ABC中,∠A,∠B都是锐角,且sinA=![]() ,tanB=
,tanB=![]() ,AB=10,求△ABC的面积.
,AB=10,求△ABC的面积.
21. (本小题满分10分)
已知一次函数的图象与双曲线![]() 交于点(
交于点(![]() ,
,![]() ),且过点(
),且过点(![]() ,
,![]() ),
),
(1)求该一次函数的解析式;
(2)描出函数草图,根据图象写出使一次函数的值大于反比例函数的值的![]() 的取值范围;
的取值范围;
22. (本小题满分12分)
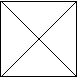
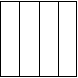
为了美化环境,在一块正方形空地上分别种植四种不同的花草.现将这块空地按下列要求分成四块:⑴分割后的整个图形必须是轴对称图形;⑵四块图形形状相同;⑶四块图形面积相等.现已有两种不同的分法:
⑴分别作两条对角线(图1) ⑵过一条边的三等分点作这边的垂线段(图2)
(图2中两个图形的分割看作同一方法)
 |  | ||||
 | |||||
|
|
请你按照上述三个要求,分别在下面三个正方形中给出另外三种不同的分割方法
(只要求正确画图,不写画法).(画对一个得4分)
 |  |  | |||
23.(本小题满分12分)
演会预算中票价定为每张100元,容纳观众人数不超过2000人,毛利润![]() (百元)关于观众人数
(百元)关于观众人数![]() (百人)之间的函数图象如图所示,当观众人数超过1000人时,表演会组织者需向保险公司缴纳定额平安保险费5000(不列入成本费用),请解答下列问题。
(百人)之间的函数图象如图所示,当观众人数超过1000人时,表演会组织者需向保险公司缴纳定额平安保险费5000(不列入成本费用),请解答下列问题。
(1)当观众不超过1000人时,毛利润![]() 关于观众人数
关于观众人数![]() 的函数解析式和成本费用
的函数解析式和成本费用![]() (百元)关于观众人数
(百元)关于观众人数![]() 的的函数解析式;
的的函数解析式;
(2)若要便这次表演会获得36000元的毛利润,那么需售出多少张门票?需支付成本费用多少元?(当观众人数不超过1000人时,表演会的毛利润=门票收入-成本费用;当观众人数超过1000人时,表演会的毛利润=门票收入-成本费用-平安保险费)。
24.(本小题满分14分)
已知抛物线![]() ,当x<1时,y随着x的增大而增大,当x>1时,y随着x的增大而减小
,当x<1时,y随着x的增大而增大,当x>1时,y随着x的增大而减小
(1)求k的值及抛物线的解析式
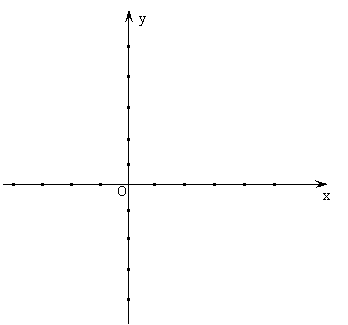
(2)设抛物线与x轴交于A、B两点(A在B的左边),抛物线的顶点为P,试求出A、B、P三点的坐标,并在下面的直角坐标系中画出这条抛物线
(3)求经过P、A、B三点的圆的圆心O‘的坐标
(4)设点G(0,m)是y轴的一个动点
①当点G运动到何处时,直线BG是⊙O‘的切线?并求出此时直线BG的解析式
 ②若直线BG与⊙O‘相交,且另一交点为D,当m满足什么条件时,点D在x轴的下方?
②若直线BG与⊙O‘相交,且另一交点为D,当m满足什么条件时,点D在x轴的下方?