常州市新桥中学2006年中考数学模拟测试七

常州市新桥中学2006年中考数学模拟测试七

班级____姓名___________得分______

一、细心填一填

1．－2的倒数=______；12的算术平方根是______；若a的绝对值为２，则a=________。

2．写出－1和2之间的任意一个无理数：　　　　　  ．

3．在比例尺为1∶40000的地图上，某经济开发区的面积为，那么，该经济开发区

的实际面积为　　　　　 （用科学记数法表示）．

4．随机抽查了某住宅小区4月份5天的用水量（单位：吨），结果分别是30、34、36、28、

32，那么，请你估计该小区4月份（30天）的总用水量约是　　　　　　  吨．

5．已知在Rt△ABC中，∠C=90°，sinA＝，则cosB=________。

6．二次函数y＝(x－2)²＋1的顶点坐标是__________,对称轴是___________,当y随x的增

大而减小时，自变量x的取值范围是_____________，将该函数的图像沿x轴向左平移两

个单位长度，所得到的图像对应的函数解析式是____________________。

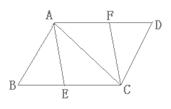
7.如图，D、E为△ABC两边AB、AC的中点，将△ABC沿线段DE折叠，使点A落在

点F处，若∠B=55°，则∠BDF=　　　 °。

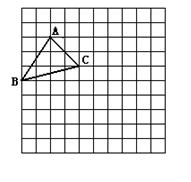
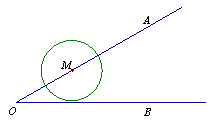
8．如图，已知∠AOB = 30°，M为OA边上一点，以M为圆心、2cm为半径作⊙M.若点M在OA边上运动，则当OM=　　  cm时，⊙M与OB相切．

第7题　　　　　　　　　　  第8题　　　　　　 　　　　　　　　　　 第9题

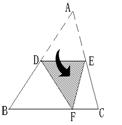
9．如图是一块由篱笆围起的面积为3π的等边三角形草地，一只羊拴在三角形顶点的柱子上，要使羊能够吃掉这块地上一半的草，则这条拴羊的绳子长至少为　　　　_______。

x	3.23	3.24	3.25	3.26
ax2+bx+c	－0.06	－0.02	0.03	0.09

10．根据下列表格的对应值：

判断方程ax²+bx+c＝0（a≠0，a，b，c为常数）一个解x的范围是_______________。

二、选择题

11．在下列实数中，是无理数的为　　　　　　　　　　　　　　　　　　  （　　 ）

A、　　　　　 B、　　　　　 C、　　　　  D、

12．下列图形中，既是轴对称图形又是中心对称图形的是　　　　　　　　  （　　 ）

			D

13. 如图是一个正方体的表面展开图，已知正方体相对两个面上的数值相同，且不相对两个面上的数值不相同，则“★”面上的数为　　　　　　　　　　　　　　 （ 　　）

A、-2　　　　　　　B、-2或3　　　　　　 C、3　　　　　   D、2或3

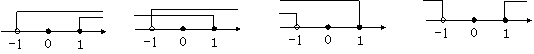14．把不等式组的解集表示在数轴上，正确的是　　　　　　　　 （　　 ）

　　　（A）　　　　　　 （B）　　　　　　  （C）　　　　　　　　 （D）

15.面积为10的正方形的边长满足下面不等式中的　　　　　　　　　　　 （　　 ）

A.1＜＜3　　　 　B. 3＜＜4　　　　 C. 5＜＜10　　　 D. 10＜＜100

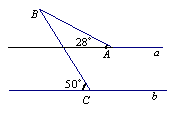
16．如图所示，直线a∥b，则∠B等于　　　　　　　　　　　　　　　　  （　　 ）

A.78°　　　　　　 B. 50°　　　　　　 C.28°　　　　　　 D.22°　

17.某圆锥的主视图是一个边长为的等边三角形，这个圆锥的侧面积是　 （　　 ）

A. 　　　B. 　　　　C. 　　　D. 　

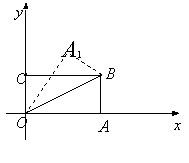
第13题　　　　　　　　　　　 第16题　　　　　　　　  第18题

18．如图，在直角坐标系中，将矩形沿对折，使点落在点处，已知,，则点的坐标是　　　　　　　　　　　　　　　　　 （　　 ）

A．（，）　　  B．（，3）　　　C．（，）　　 D．（，）

三、认真答一答

19．(1)计算:(　 (2)化简：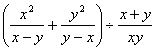

20．（1）解方程：+=1　　 （2）解不等式组并写出整数解

21．已知,如图ABCD中，AE、CF分别是∠BAC和∠ACD的平分线.

　　求证:AE=CF.

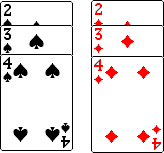
22．如图是从一副扑克牌中取出的两组牌，分别是黑桃2、3、4和方块2、3、4，将它们

背面朝上分别重新洗牌后，从两组牌中各摸出一张，那么摸出的两张牌的牌面数字之和等

于5的概率是多少？请你用列表或画树状图加以分析说明．

23．某校为了选拔一名运动员参加区运动会100m赛跑，对甲、乙两名选手进行了六次选拔测试，成绩如图所示：

（1）根据右图所提供的信息完成下表：

	平均成绩	方差
甲		0.027
乙	11.0	0.020

（2）如果你是教练，会选择哪位运动员

参加比赛？请说明理由．

24．在方格纸中作图：

(1)将△ABC向右平移4个单位得△A'B'C'；

(2)将△A'B'C'绕点C’逆时针旋转90,得△A”B”C”；

(3)如果建立直角坐标系，使点B的坐标为（-5，0），

点B’ 的坐标为（-1，0），则点B” 的坐标为 　　　.

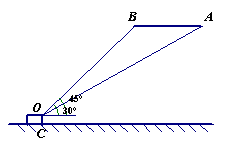
25．如图，一架飞机以每小时900千米的速度水平飞行，某个时刻，从地面控制塔O（塔高300m）观测到飞机在A处的仰角为30°，5分钟后测得飞机在B处的仰角为45°，试确定飞机的飞行高度．（，结果精确到1km）

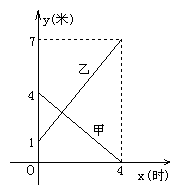
26．某学校有甲、乙两个长方体的蓄水池，将甲池中的水以每小时8立方米的速度注入乙池，甲、乙两个蓄水池中水的深度y(米)与注水时间x(时)之间的函数图象如图所示，结合图象回答下列问题：

(1)分别求出甲、乙两个蓄水池中水的深度y与注水时间x之间的函数关系式；

(2)求注水多长时间甲、乙两个蓄水池水的深度相同；

(3)求注水多长时间甲、乙两个蓄水池的蓄水量相同．

四、动脑想一想

27．阅读后填空：在形如的式子中，我们已经研究过两种情况：

①已知a和b，求N，这是乘方运算；

②已知b和N，求a，这是开方运算；

现在我们研究第三种情况：已知a和N，求b，我们把这种运算叫做对数运算.

定义：如果（a＞0，a≠1，N＞0），则b叫做以a为底N的对数，记作.

例如：求，因为＝8，所以=3；又比如：∵ ，∴ .

（1）根据定义计算：

①＝＿＿＿＿；②=　　　 ；

③如果，那么x＝＿＿＿＿.

（2）设则(a＞0,a≠1,M、N均为正数),

∵，∴ ∴，

即

这是对数运算的重要性质之一，进一步，我们还可以得出：

＝　　　　　　　　　　　　　　　　  .

（其中M₁、M₂、M₃、……、M_n均为正数，a＞0，a≠1）

（3）请你猜想：　　　　　　　　 (a＞0,a≠1,M、N均为正数).