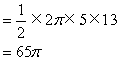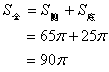一.教学内容:
圆中计算问题中考题选讲
二. 教学重点:
1. 求阴影部分的面积。
2. 解决实际问题。
【典型例题】
一、阴影部分面积求解的几种方法:
例1. 如图,A是半径为2的⊙O外一点,OA=4,AB是⊙O的切线,点B是切点,弦BC∥OA,连结AC,求图中阴影部分的面积。
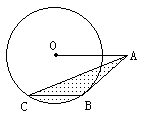
分析:图中阴影部分可看作弓形BC面积与三角形ABC面积的和,而△ABC不是Rt△,所以考虑借助OA∥BC将△ABC移形,连接OC、OB,则S△OCB=S△ACB。
则阴影部分面积为扇形AOB面积。
解:连接OB、OC,因为BC∥OA
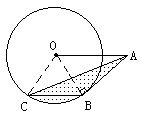
所以△ABC与△OBC在BC上的高相等
所以![]()
所以![]()
又∵AB是⊙O的切线
所以OB⊥AB,而OB=2,OA=4
所以∠AOB=60°,
由BC∥OA得∠OBC=60°
所以△OBC为等边三角形,∠BOC=60°
![]()
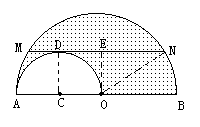
例2. 如图,扇形AOB的圆心角为直角,若OA=4,以AB为直径作半圆,求阴影部分的面积。
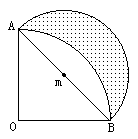
分析:图中阴影部分面积为:
以AB为直径的半圆面积减去弓形AmB面积;
而弓形面积等于扇形AOB面积减去△AOB面积。
解:∵OA=4cm,∠O=90°,OB=4cm
∴![]()
又![]()
所以![]()
而![]()
故![]()
例3. 如图,⊙A、⊙B、⊙C、⊙D、⊙E相外离,它们的半径都是1,顺次连接五个圆心得到五边形ABCDE,则图中五个扇形(阴影部分)的面积之和是多少?

分析:五个扇形的圆心角分别为
![]()
而![]()
解:设这个五个扇形的圆心角的度数分别为![]()
∵五边形ABCDE内和角等于540°
则![]()
五个扇形面积之和等于
![]()
![]()
![]()
![]()
例4. 已知直角扇形AOB,半径OA=2cm,以OB为直径在扇形内作半圆⊙M,过M引MP∥AO交![]() 于P,求
于P,求![]() 与半圆弧及MP围成的阴影部分的面积S阴。
与半圆弧及MP围成的阴影部分的面积S阴。
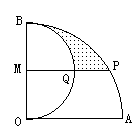
分析:此阴影部分不是一个规则图形,不能用公式直接求解。所以考虑将它分割为可求图形的面积求解。
解:连接OP
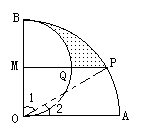
∵OA⊥OB,又∵MP∥OA
∴MP⊥OB,又∵OM=BM=1
OP=OA=2
∴∠1=60°,∠2=30°
∴![]()
∴![]()
![]()
设PM与半圆⊙M交于Q
∴![]()
∴![]()
![]()
例5. 如图,在两个半圆中,大圆的弦MN与小圆相切于点D,MN∥AB,MN=8cm,ON、CD分别是两圆的半径,求阴影部分的面积。
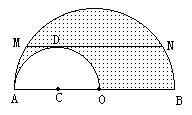
分析:![]()
所以关键是求⊙O半径OB或OM或ON
⊙C半径AC或CO或CD
而MN为⊙C切线,CD⊥MN且CD为⊙C半径
解:过O作OE⊥MN于E,则OE平分MN
![]()
∵MN∥AB可得四边形EOCD为矩形
所以OE=CD,连接ON
在Rt△EON中
![]()
ON=4
![]()
二、实际问题
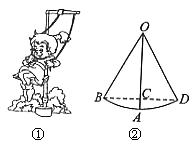
例1. 一个小孩荡秋千,如图所示,秋千的链子的长为OA=2.5m,当秋千向两边摆动时,摆角∠BOD恰好为60°,并且两边摆动角度相同。
求:(1)秋千摆至最高位置时与其摆至最低位置时的高度之差。
(2)秋千从B点摆动到D点所走过的路程(结果精确到0.01m)
分析:抽象出几何图形
OB=OD=OA为秋千的链子长
OA为秋千摆至最低位置
OB与OD为秋千摆至最高位置
AC为这两个位置的差
![]() 为摆动的路程。
为摆动的路程。
解:连接BD交OA与C,则OA⊥BD于C
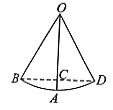
![]() ,∠BOD=60°
,∠BOD=60°
则∠BOC=∠COD=30°
Rt△OCD中,![]()
![]() 米
米
(2)![]() 的长l=
的长l=![]() 米
米
答:(1)略。(2)略。
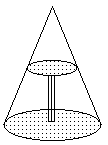
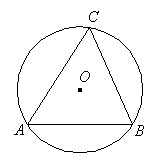
例2. 某燃料公司的院内堆放10个外径为1米的空油桶,为了防雨,防雷,需搭建简易防雨棚,这个防雨棚的高度最低应为多少米?
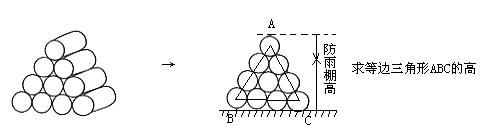
分析:实际问题抽象成几何模形,用几何图形解决。
解:△ABC为等边三角形
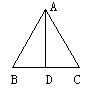
AB=6个半径=3米
![]() 米
米
则防雨棚高度等于![]() 米。
米。
答:高至少为![]() 米。
米。
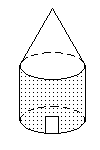
例3. 新疆哈萨克民族是一个游牧民族,喜爱居住毡房,毡房的顶部是圆锥形,如图所示,为防雨需要在毡房顶部铺上防雨布,已知圆锥的底面直径是5.7m,母线长是3.2m,铺满毡房顶部至少需要防雨布(精确到1m2)( )
A. ![]() B.
B.
![]() C.
C. ![]() D.
D.
![]()
分析:求圆锥侧面积
解:∵![]()
![]()
![]()
![]()
选B。
例4. 如图,有一直径是![]() 米的圆形铁皮,要从中剪出圆心角是90°的一个最大扇形ABC,求(1)被剪掉阴影部分的面积。(2)用所留的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径是多少?(结果可用根号表示)。(3)求圆锥的全面积。
米的圆形铁皮,要从中剪出圆心角是90°的一个最大扇形ABC,求(1)被剪掉阴影部分的面积。(2)用所留的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径是多少?(结果可用根号表示)。(3)求圆锥的全面积。
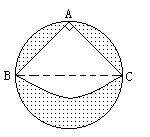
分析:阴影部分面积是圆的面积减去一个圆心角为90°的扇形面积,其关键是要求出扇形的半径,由弧长等于底面周长可求出半径。
解:(1)连接BC
因为∠A=90°,所以BC为⊙O的直径,BC![]()
在Rt△ABC中,![]()
又![]()
![]()
![]()
(2)设圆锥底面半径为r,则![]() 长为
长为![]()
所以![]()
(3)![]()
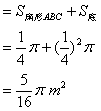
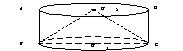
例5. 如图,这是圆桌上方的灯泡(看作一个点)发出的光线,照射桌面后,在地面上形成阴影(图形)的示意图,已知桌面的直径为1.2m,桌面距离地面1m,若灯泡距离地面3m,则地面上阴影部分的面积是多少?
分析:灯泡的光线射在地面上,形成的阴影可体会成一个圆锥,要求阴影的面积,即求底面圆的半径即可。
解:由已知可作轴截面
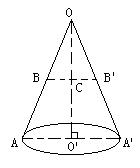
其中![]()
从而OC=2m,BC=0.6
由BC∥OA得:
![]()
![]()
所以![]()
![]()
【模拟试题】(答题时间:40分钟)
一. 选择题。
1. 在半径为3的⊙O中,弦MN=3,则![]() 的长为( )
的长为( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
2. 扇形的周长为16,圆心角为![]() ,则扇形的面积为( )
,则扇形的面积为( )
A. 16 B.
32 C.
64 D.
![]()
3. 如果圆柱的高为20厘米,底面半径是高的![]() ,那么这个圆柱的侧面积是( )
,那么这个圆柱的侧面积是( )
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
4. 已知圆锥的底面半径是3,高是4,则这个圆锥的侧面展开图的面积是( )
A. ![]() B.
B. ![]() C.
C.
![]() D.
D. ![]()
5. 如图,ABCD是正方形,边长为a,以B为圆心,以BA为半径画弧,则阴影面积为( )
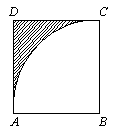
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
二. 填空题。
1. 直径为12cm的圆,60°圆周角所对的弧的弧长为___________厘米。
2. 如图,在△ABC中,∠ACB=90°,∠B=15°,以C为圆心,CA为半径的圆交AB于D点,若AC=6cm,则![]() 的长为___________厘米。
的长为___________厘米。
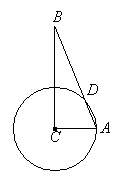
3. 一个扇形的弧长为![]() 厘米,面积为
厘米,面积为![]() cm2,则该扇形的圆心角为___________度。
cm2,则该扇形的圆心角为___________度。
4. 已知圆柱母线与底面圆的直径相等,且底面积为![]() ,则圆柱的侧面积为_________
,则圆柱的侧面积为_________ ![]() 。
。
5. 若圆锥的母线长为6cm,侧面展开图是圆心角为300°的扇形,则圆锥底面半径为___________cm。
6. 圆锥底面半径为4 cm,母线长为24cm,则侧面展开图中扇形的圆心角为__________。
7. 若用半径为15cm,圆心角为216°的扇形围成一个圆锥的侧面,则这个圆锥的高为___________cm。
三. 解答题。
1. 已知![]() 的长为
的长为![]() 厘米,所对的圆周角∠ACB=60°,求弦AB的长。
厘米,所对的圆周角∠ACB=60°,求弦AB的长。
2. 如图,在△ABC中,∠BAC=105°,∠B=45°,![]() ,AD⊥BC,垂足为D,以A为圆心,AD为半径画弧
,AD⊥BC,垂足为D,以A为圆心,AD为半径画弧![]() ,求图中阴影部分的面积。
,求图中阴影部分的面积。
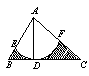
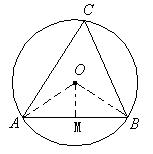
3. 如图,![]() 中,∠C=90°,AC=BC=
中,∠C=90°,AC=BC=![]() cm,分别以A、B、C为圆心画弧,使
cm,分别以A、B、C为圆心画弧,使![]() 所在的圆两两外切。求:
所在的圆两两外切。求:
(1)![]() 的长;
的长;
(2)阴影部分的面积。
![]()
4. 如图,圆柱的高为12cm,底面直径为10cm,求图中圆锥的全面积。
【试题答案】
一. 选择题。
1. B 2. A 3. B 4. B 5. D
二. 填空题。
1. ![]() 2.
2.
![]()
3. 150 4.
![]()
5. 5 6. 60°
7. 12
三. 解答题。
1. 解:连结OB,OA,并过O作OM⊥AB于M
∴AM=BM=![]()
∵∠ACB=60°,∴∠AOB=120°
∵![]()
![]()
在Rt△BOM中
∠AOM=60°
![]()
∴![]()
2. 解:∵△ABC中,∠B=45°,AD⊥BC,
∠BAC=105°
∴∠BAD=45°,∠DAC=60°
∴BD=AD=2,![]()
∴BC=2+![]()
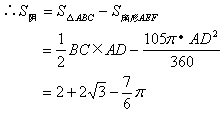
3. 解:(1)设BF=x,CF=y,AE=z
∵∠C=90°,AC=BC=![]() ∴AB=2
∴AB=2
则有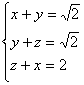
![]()
∴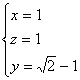
∴![]()
![]()
![]()
![]()
(2)![]()
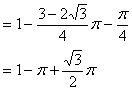
4. 解:连结![]() ,
,
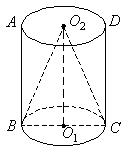
∵BC=10,∴O1C=5
又∵O1O2=12
∴Rt![]() 中
中
![]()
∴![]()