2005年中考数学复习同步检测（21） 姓名
（四边形2）
一．填空题：
1．平行四边形ABCD的周长为50cm，且AB: BC = 3:2，则AB=______cm，BC=______cm.；
2．在平行四边形ABCD中，∠A等于∠B的3倍，则∠B________°, ∠C_________°；
3．已知矩形两条对角线的夹角为60°，较短的边长为4.5cm，则
对角线的长是_______。
4．已知菱形的周长是24cm，一条较小的对角线的长是6cm，则该菱
形较大的内角是________，较长的对角线与边的夹角是_______。
5．若直角梯形被一条对角线分成两个等腰直角三角形,那么这个梯形
中除两个直角外,其余两个内角的度数分别为 
和 ；
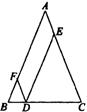
6．如图，在△ABC中，AB=AC=8cm,D是BC上任意一点，DE∥AB，
DF∥AC,F、E分别在AB、AC上，则平行四边形AFDE的周长为__________；
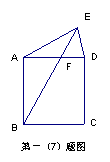
7．如图，E为正方形ABCD外一点,AE=AD,BE交AD于F，
∠ADE=75°, 则∠AFB=________________°。
8．在梯形ABCD中,AD∥BC,且∠A=2∠B=3∠C，则∠D=____________°
9．平行四边形的四个内角平分线围成了一个____________；矩形的四个内角平分线围成了一个__________________；菱形的四个内角平分线____________________________；
10．要说明一个四边形是菱形,可以先说明这个四边形
是 形,再说明
(只需填写一种方法)
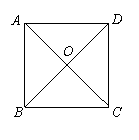
11．如图,正方形ABCD的对线AC、BD相交于点O.
那么图中共有 个等腰直角三角形.
12．把“直角三角形、等腰三角形、等腰直角三角形”填入下列相应的空格上.
(1)正方形可以由两个能够完全重合的 拼合而成;
(2)菱形可以由两个能够完全重合的 拼合而成;
(3)矩形可以由两个能够完全重合的 拼合而成.
13．平行四边形的周长为24
,相邻两边长的比为3:1,那么这个平行四边形较短的边长为
；
14．根据图中所给的尺寸和比例,可知这个“十”字标志的周长为
；
 | |||
 | |||
(第14题) (第16题)
15．已知菱形的两条对角线长为12和6,那么这个菱形的面积为
；
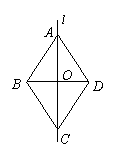
16．如图,
是四边形ABCD的对称轴,如果AD∥BC,有下列结论: (1)AB∥CD;(2)AB=CD;(3)AB
BC;(4)AO=OC.其中正确的结论是
.(把你认为正确的结论的序号都填上)
17．已知：平行四边形ABCD的周长为30cm,AB：BC=2：3，则AB= ；
18．若一个多边形的内角和是外角和的5倍，则这个多边形是 边形；
19．在梯形ABCD中，两底AB=14cm，DC=6Ccm，两底角∠A=30°，∠B=60°，则腰
BC=
；
20．菱形两条对角线分别长4cm，8cm，则菱形边长为 ；
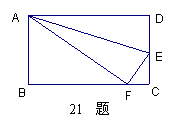
21．如图，把边长为AD=12cm，AB=8cm的矩形沿着AE为折痕对折使点D落在BC上点F处，则DE= cm;
22．一个正正多边形每一个内角都等于它相邻的外角的
一半，这是一个正 边形；
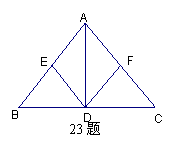
23．如图，在⊿ABC中，AD⊥BC于D，E、F分别是
AB、AC的中点，当⊿ABC满足条件 时， AEDF是菱形；
24．在四边形ABCD中，若AB∥CD，AD=BC，则四边
形ABCD是 ；
25．对角线
的四边形是平行四边形；对角线
的平行四边形是矩形；对角线 的
平行四边形是菱形；
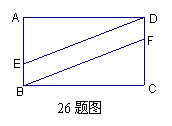
26．如图,在矩形ABCD中,BF∥DE,若AD=12cm,AB=7cm ,
且AE：EB=5：2,则S四边形EBFD= 。
二．选择题：
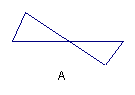
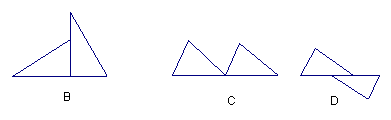27．观察下列四张图形，其中与另外三张不同的
（ ）
 |
28．如图，下列图形中属于中心对称图形的是 （ ）
29．如图，在平行四边形ABCD中，∠BAD的角平分线交BC于点E，且AE=BE，则∠BCD的度数为 （ ）A． 30° B. 60° C. 120° D. 150°
30．四边形ABCD中,∠A=∠C,∠B=∠D，则下列结论中错误的是 （ ）
A． ∠A=∠B B. AB=CD C. 对角线互相平分 D. AD∥BC
31．下列说法中正确的是 （ ）
A.一个角是直角，两条对角线相等的四边形是矩形；
B.一组对边平行且有一个角是直角的四边形是矩形；
C.对角线互相垂直的平行四边形是矩形；
D.一个角是直角且对角线互相平分的四边形是矩形。
32．已知平行四边形一边长为10，一条对角线长为6，则它的另一条对角线
的取值范围（ ）
A. 4＜＜6
B. 14＜＜26 C. 12＜＜20 D. 无法确定
33．两条对角线互相垂直平分且相等的四边形是 （ ）
A. 菱形 B. 矩形 C. 平行四边形 D. 正方形
34．若四边形四角度数之比为1：2：2：3，则此四边形为 （ ）
A． 梯形 B 正方形 C 直角梯形 D 平行四边形
35．如果一个四边形是中心对称图形，那么这个四边形一定是 （ ）
A． 菱形 B． 正方形 C． 矩形 D． 平行四边形
36．在线段、角、等边三角形、等腰三角形、平行四边形、矩形、菱形、正方形、圆、等腰梯形这十种图形中,既是轴对称图形又是中心对称图形的共有 （ ）
A. 4种 B. 5种 C. 7种 D. 8种
37．下列说法中,错误的是 （ ）
A. 平行四边形的对角线互相平分 B. 对角线互相平分的四边形是平行四边形
C. 菱形的对角线互相垂直 D. 对角线互相垂直的四边形是菱形
38．给出四个特征①两条对角线相等；②任一组对角互补；③任一组邻角互补；④是轴对称图形但不是中心对称图形,其中属于矩形和等腰梯形共同具有的特征的共有 （ ）
A. 1个 B. 2个 C. 3个 D. 4个
39．如果一个四边形的两条对角线互相平分,互相垂直且相等,那么这个四边形是 （ ）
A. 矩形 B. 菱形 C. 正方形 D. 菱形、矩形或正方形
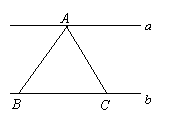
40．如图,直线
∥
,A是直线上的一个定点,线段BC在直线上移动,那么在移动过程中
的面积
（ ）
|
 | |||
| |||
(第40题) (第41题) (第42题)
41．如图,矩形ABCD沿着AE折叠,使D点落在BC边上的F点处,如果
,则
等于
（ ）
A. 
B. 
C. 
D. 
42．如图,在中,AB=AC=5,D是BC上的点,DE∥AB交AC于点E,DF∥AC交AB于点F,那么四边形AFDE的周长是
（ ）
A. 5 B. 10 C. 15 D. 20
43．已知四边形ABCD中,AC交BD于点O,如果只给条件“AB∥CD”,那么还不能判定四边形ABCD为平行四边形,给出以下四种说法:
(1)如果再加上条件“BC=AD”,那么四边形ABCD一定是平行四边形;
(2)如果再加上条件“
”,那么四边形ABCD一定是平行四边形;
(3)如果再加上条件“AO=OC”,那么四边形ABCD一定是平行四边形;
(4)如果再加上条件“
”,那么四边形ABCD一定是平行四边形
其中正确的说法是 （ ）
A. (1)(2) B. (1)(3)(4) C. (2)(3) D. (2)(3)(4)
44．能够找到一点，使该点到各边距离都相等的是 （ ）
① 平行四边形 ②菱形 ③矩形 ④正方形 ⑤三角形
A
①② B ②③④⑤ C ②④ D ②④⑥
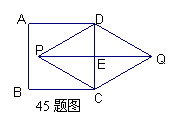
45．如图，正方形ABCD的边长为3，以CD为一边向CD两
旁作等边⊿PCD和等边⊿QCD。则PQ的长是 （ ）
A 
B 
C 3
D 6
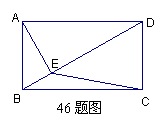
46．如图，在矩形ABCD中，BC=2，AE⊥BD于E，若
∠BAE=30°，则S△ECD= （ ）
A 2 B
C 3 D 6
47．下列图形中，是中心图形又是轴对称图形的有 （ ）
① 平行四边形；②菱形；③矩形；④正方形；⑤等腰梯形；⑥线段；⑦角；
A 2个 B 3个 C 4个 D 5个
48．一个平行四边形绕着它对角线的交点旋转90能够与它本身重合，则该四边形是 （ ）
A 矩形 B 菱形 C 正方形 D 无法确定
49．用一批形状完全相同的正多边形的地板砖铺地面，要求顶点聚在一起，且砖与砖之间不留空隙，现有：①正三角形；②正四边形；③正五边形；④正六边形；四种形状的地板砖，则符合要求的有：
A ①②③ B ①②④ C ②③④ D ①③④
50．菱形周长为40，两邻边所夹锐角为30°，则菱形的面积为 （ ）
A 30 B 40 C 50 D 60
51．顺次连结矩形的各边中点，所得四边形是 （ ）
A 平行四边形 B 矩形 C 菱形 D ）正方形
52．有两个角相等的梯形是 （ ）
A 等腰梯形 B 直角梯形 C 一般梯形 D 等腰梯形或直角梯形；
三．计算题：
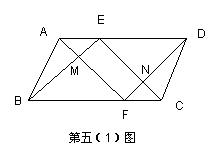53．如图，平行四边形ABCD中，EF为边AD、BC上的点，且AE=CF，连结AF、EC、BE、DF交于M、N，试说明：MFNE是平行四边形
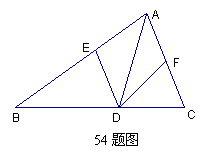
54．已知：如图，AD是△ABC的角平分线，DE∥AC与E，DF∥AB交AC于F，请判断四边形AEDF的形状，并说明理由。
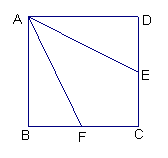
55．正方形ABCD中，AE=CF，则四边形BEDF是菱形吗？请说明理由。
56．已知平行四边形ABCD中，AB=8，BC=10，∠B=45°,求平行四边形ABCD的面积。
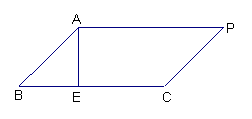
57．如图，正方形ABCD的边长为2a,E.是CD的中点，F在BC边上移动，问当F移动到什么位置时，AE平分∠FAD？请证明你的结论。
58．在梯形ABCD中，AD∥BC，AD+BC=CD ，M是AB的中点，试问：DM、CM是否分别是∠ADC和∠DCB的平分线？说明理由？
