2005年中考数学复习同步检测（38） （模拟题2） 姓名
2005届初中升学数学样卷（二）
一．填空题：（每小题3分，共30分）
1．
；
2．2003年5月19日，国家邮政局特别发行“万众一心 抗击‘非典’”邮票，收入全部捐赠给卫生部门，用以支持抗击“非典”斗争，其邮票发行量为枚，用科学记数法表示正确的是 ；
3．分解因式：
；
4．函数函数
中自变量
的取值范围是
；
5．从甲、乙、丙三个厂家生产的同一种产品中各抽取8件产品，对其中使用寿命跟踪调查．结果如下：（单位：年） 甲：3，4，5，6，8，8，8，10 乙：4，6，6，6，8，9，12，13 丙：3，3，4，7，9，10，11，12 三个厂家在广告中都称该产品的
使用寿命是8年，请根据结果判断厂家在广告中分别运用了平均数、
众数、中位数中的哪一种集中趋势的特征数： 图A
甲 ，乙 ，丙 ；
6．二次函数
，当
时，
;且
随的增大而减小；
图B
7．两个长、宽各为
米、
米的矩形花圃，都修建了形状不同的一条宽为
米的小路，问：这两条小路的面积是否相等？
（填相等或不相等），若相等，面积是 ；
8．五个正整数从小到大排列，若这组数据的中位数是4，唯一众数是5，则这五个正整数的和为
；
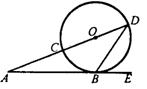
9．已知：如图，CD是⊙O的直径，AE切⊙O于点B，DC的延长
线交AB于点A，∠A =
，则∠DBE＝_________；
10．党的十六大提出全面建设小康社会，加快推进社会主义现代化，
力争国民生产总值到2020年比2000年翻两番。在本世纪的头二十年
（2001年～2020年），要实现这一目标，以十年为单位计算，设每
个十年的国民生产总值的增长率都是，那么满足的方程为
；
二．选择题（每小题4分，共24分）
在每个小题给出的四个备选答案中，只有一个是符合题目要求的，请把所选答案前的字母填写在下表中。
| 11 | 12 | 13 | 14 | 15 | 16 |
11．下列各式中，正确的是
（A） 
（B）
（C）
（D）
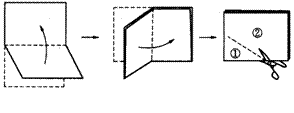12．将一张矩形纸对折再对折（如图），然后沿着图中的虚线剪下，得到①、②两部分，将①展开后得到的平面图形是、
A 矩形 B 三角形
C 梯形 D 菱形
13．某中学人数相等的甲、乙两班学生参加了同一次数学测验，班平均分和方差分别为
＝82分，
＝82分，
＝245，
＝190，那么成绩较为整齐的是
（A） 甲班 （B） 乙班 （C） 两班一样整齐 （D）无法确定
14．某商场的营业额1999年比1998年上升10％，2000年比1999年上升10％，而2001年和2002年连续两年平均每年比上一年降低10％，那么2002年的营业额比1998年的营业额
（A） 降低了2％ （B） 没有变化 （C） 上升了2％ （D） 降低了1.99％
15．下列各图中，每个正方形网格都是由四个边长为１的小正方形组成，其中阴影部分面积为
的是
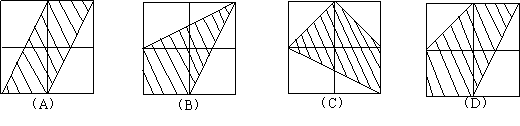
16．某村办工厂今年前5个月生产某种产品的总量c（件）关于时间t（月）的函数图象如图所示，则该厂对这种产品来说
（A） 1月至3月每月生产总量逐月增加，4、5两月每
月生产总量逐月减少
（B） 1月至3月每月生产总量逐月增加，4、5两月每
月生产总量与3月份持平
（C）1月至3月每月生产总量逐月增加，4、5两月均停止生产
（D）1月至3月每月生产总量不变， 4、5两均停止生产
三．解答题：（96分）
17．（7分）计算 
18．（10分）化简求值：
；
.
19．（8分）某电视机场2000年生产一种彩色电视机，每台成本3000元，由于该厂不断进行技术改造，连续两年降低成本，到2002年这种彩色电视机成本仅1920元，问平均每年降低成本百分之几？
20．（10分）一条对角线平分一个平行四边形的内角，这个平行四边形会是菱形吗？为什么？
21．（12分）如图，割线ABC与⊙O相交于B、C两点，D为⊙O上一点，E为BC的中点，OE交BC于F，DE交AC于G，∠ADG＝∠AGD.
⑴ 求证：AD是⊙O的切线；
⑵ 如果AB=2，AD=4，EG=2，求⊙O的半径．
22．（9分）如图所示：爬上小山有两条石阶路，（1）哪条路走起来更舒适？（2）运用所学统计知识，设计一条舒适的石阶路，简要说明理由。
 |
23．（10分）如图：已知一次函数
的图象与轴、轴分别交于
、
两点，且与反比例函数
的图象在第一象限交于
点，
⊥轴，垂足为
，
若
（1）求点、、的坐标；（2）求一次函数与反比例函数的解析式；；
y
C
B
x
A O D
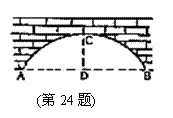24．（10分）有一个拱桥是圆弧形，他的跨度为60
，拱高为18，当洪水泛滥跨度小于30时，要采取紧急措施。若拱顶离水面只有4时，问是否要采取紧急措施？
25. （10分）如图，一单杆高
，两立柱之间的距离为
，将一根绳子的两端栓于立柱与铁杠结合处，绳子自然下垂呈抛物线状。
（1）一身高
的小孩站在离立柱
处，其头部刚好触上绳子，求绳子最低点到地面的距离，
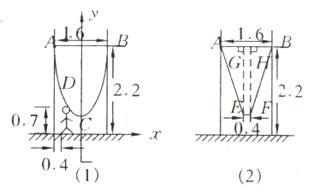（2）为供孩子们打秋千，把绳子剪断后，中间系上一块长为
米的木板，除掉系木板用去的绳子后，两边的绳子正好各为2米，木板与地面平行，求这时木板到地面的距离。（供选用数据：
，
，
）
26．（10分）已知：如图，⊙O与⊙P相交于A、B两点，点 P在⊙O上，⊙O的弦AC切⊙P于点A，CP及其延长线交⊙P于D、E，过点 E作EF⊥CE交CB的延长线于F。
（1）求证：BC是⊙P的切线；
（2）若CD＝2，CB＝
，求EF的长；
（3）求以BP、EF为根的一元二次方程；
2005届初中升学数学样卷（二）答案
一．填空题：
1．
； 2．
枚； 3．
； 4．
且
；
5．众数，平均数，中位数； 6．
； 7．相等，
米
； 8．17或18或19；
9．
；
10．
；
二．选择题
在每个小题给出的四个备选答案中，只有一个是符合题目要求的，请把所选答案前的字母填写在下表中。
| 11 | 12 | 13 | 14 | 15 | 16 |
| A | D | B | D | D | B |
三．解答题：
17．原式=
18．原式
当
时，原式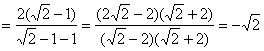
19．
解：设平均每年降低成本百分数为，根据题意得：
（不符题意，舍去），
答：平均每年降低成本为
。
20.本题证法多种，要求：1、写出已知，求证、画出图形，2、有完整的证明过程，3、有结论。
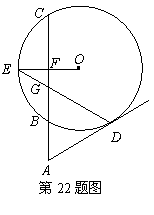21．如图，割线ABC与⊙O相交于B、C两点，D为⊙O上一点，E为BC的中点，OE交BC于F，DE交AC于G，∠ADG＝∠AGD.
⑴求证：AD是⊙O的切线；
⑵如果AB=2，AD=4，EG=2，求⊙O的半径．
|
∴OE⊥BC于F．
∴∠AGD+∠ODE＝∠EGF+∠OED
＝90°．……………………2分
连结OD．则OD＝OE，
∴∠ODE＝∠OED．……………………3分
∵∠AGD=∠ADG，
∴∠ADG＋∠ODE=90°，即OD⊥AD.
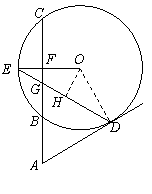∴AD是⊙O的切线．……………………5分
⑵由AD=4，AB=2，AD2=AB·AC，得AC=8．……………………6分
∵AD=AG，∴BG=2，CG=4.
由EG=2，EG·GD=BG·CG，得DG=4．…………………………7分
∴AD=DG=GD，∴∠ADG=60°．
作OH⊥ED于H，则∠EOH=60°．…………………………………8分
在Rt△OEH中，EH=
，……………………………9分
∴OE＝
＝
．
即⊙O的半径为．………………………………………………10分
22．解：（1）
，
但：
，
，
∴
，
∴走甲路更舒适。
（2）设计石阶路的每一级石阶高度为15（
），由于高度一致，平均数一致，所以方差为零，即
，这样的石阶路走起来更舒适。
23．如图：已知一次函数的图象与轴、轴分别交于、两点，且与反比例函数的图象在第一象限交于点，⊥轴，垂足为，
若（1）求点、、的坐标；（2）求一次函数与反比例函数的解析式；；
y
C
B
x
A O D
解：（1）∵OA = OB = OD = 1，∴A（
，0）、B（0，1）、D（1，0）；
（2）∵过A、B两点，∴
∴所求一次函数为
，
∵C（1，）在上，∴C（1，2）也在上，∴
，
∴所求反比例函数为：
，
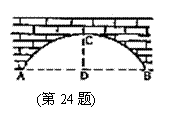24．（10分）有一个拱桥是圆弧形，他的跨度为60，拱高为18，当洪水泛滥跨度小于30时，要采取紧急措施。若拱顶离水面只有4时，问是否要采取紧急措施？
解：作出圆弧形的圆心O，
在Rt⊿OAD中，
，而OA =
，AD = 30，CD = 18
∴
∴
当拱顶里水面
米时，水面所在弦的弦心距为：
米，设水面所在的弦为，由勾股定理可知：
，∴
，负值舍去，∴
∴不用采取紧急措施。
25. （10分）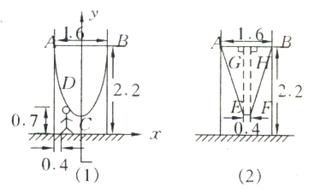
为供孩子们打秋千，把绳子剪断后，中间系上一块长为米的木板，除掉系木板用去的绳子后，两边的绳子正好各为2米，木板与地面平行，（1）求绳子未剪断时最低点到地面的距离；（2）求剪断绳子系上木板时，木板到地面的距离。（供选用数据：，，）
解：（1）如图，建立直角坐标系，
设二次函数为：
∵D（
，
），
B（
，
）
∴
∴
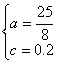，∴绳子最低点到地面的距离为
米。
（2）分别作EG⊥AB于G，EH⊥AB于H，
AG =
在Rt⊿AGE中，
∴
（米）
∴木板到地面的距离约为
米。
26．（10分）已知：如图，⊙O与⊙P相交于A、B两点，点 P在⊙O上，⊙O的弦AC切⊙P于点A，CP及其延长线交⊙P于D、E，过点 E作EF⊥CE交CB的延长线于F。
（1）求证：BC是⊙P的切线；
（2）若CD＝2，CB＝，求EF的长；
（3）求以BP、EF为根的一元二次方程；
解：（1）∵点 P在⊙O上。连结PB，
∵CP为直径，∴∠CPB =
，
∴PB⊥CB，∵B在⊙P上，
∴CB是⊙P的切线。
（2）∵CB是⊙P的切线，∴
，∵
，
∴
，∴
，∴
，
∴在⊙P中，
，
在Rt⊿CPB中，
，
，∴
，
∵EF⊥CE，∴∠FEC =∠CBP =，∠FCE =∠PCB，∴⊿FCE∽⊿PCB，
∴
，而，
，，∴
，∴
（3）∵
，
∴所求以
为根的方程是：