梅州市2005年中考数学模拟试题（一）
班级: 姓名: 座号: 评分:
一、填空题(每小题3分，共30分)
1.计算：(-3)2= ．
2.一种细菌的半径是0．000 0 26 m，用科学记数法表示这个数是 m．
3.函数y=
中自变量x的取值范围是 ．
4.点P(3，5)关于y轴对称的点的坐标是 ．
5.十边形的内角和等于 ．
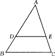6.如图，在△ABC中，如果DE∥BC，AD=2，AB=3，那么△ADE与△ABC的相似比是 ．
7.如果菱形的一条对角线长是12cm，面积是30 cm2，那么这个菱形的另一条对角线长
是 cm．
8.如果圆柱的底面半径是3cm，母线长8 cm，那么这个圆柱的侧面积是 cm2(结果保留π)．
9.如图，在△ABC中，点D在A B上，再添加一个适当的条件
，使△ACD∽△ABC．(只需填写满足要求的一个条件即可．)
10.观察下列∠愤序排列的等式：1×2-1=12，2×3-2=22，3×4—3=32，4×5 4=42，…．猜想：第n个等式(n为正整数)应为
二、选择题(每小题3分，共15分)
11.下列运算正确的是( )．
(A)a2a3=a6 (B)(a2)3=a6 (C)a6÷a2=a3 (D)a6-a2=a4
12.下列图形中，是中心对称图形但不是轴对称图形的是( )．
(A)等边三角形 (B)平行四边形 (C)等腰梯形 (D)圆
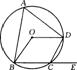13.如图，四边形ABCD内接于⊙O，如果它的一个外角∠DCE=64°，那么∠BOD=( )．
(A)128° (B)100°(C)64° (D)32°
14.对于函数y=
，下列判断正确的是( )．
(A) 图象经过点(-1，3)
(B)图象在第二、四象限
(c)图象所在的每个象限内，y随x的增大而减小
(D)不论x为何值时，总有y>O
15.某服装商同时卖出两套服装，每套均卖16 8元，以成本计算，其中一套盈利20％，另一套亏本20％，则这次卖出的两套服装中，服装商( )．
(A)盈利14元 (B)盈利37．2元
(C)亏本14元 (D)既不盈利也不亏本
三、解答下列各题(每小题6分，共24分)
16.计算：20040--
+
+
17.计算：
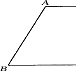
18.如图，在直角梯形ABCD中，已知底AD=6 cm，BC=11cm，腰CD=12cm，求这个直角梯形的周长．
 |
19.如图，已知在△ABC中，∠ABC=∠ACB，∠ABC的平分线交AC于点D
(1)请在图5中用尺规作∠ACB的平分线(不写作法，保留作图痕迹)；
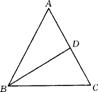(2)∠ACB的平分线交AB于点E，证明BD=CE．
四、(第20、21题各7分，第22、23题各8分，共3 O分)
20.用换元法解方程：
21.2004年“五一”黄金周，广州市共接待游客5 00万人次，旅游收入225 400万元，其中接待过夜游客和不过夜游客平均每人次旅游收入各是136 1元和17 2元．求过夜游客和不过夜游客各是多少万人次?(精确到万位)．
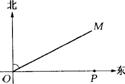
22.如图6，P市气象台预报，．一台风中心在P市正西方向8 00千米的0处，
正迅速向北偏东6 3°的OM方向移动，距台风中心35 0千米的范围内为受台风影响的区域，问P市是否受到这次台风的影响?
 |
23.已知关于x的一元二次方程2x2+4x+m-1=0有两个非零实数根．
(1)求m的取值范围；
(2)两个非零实数根能否同为正数或同为负数?若能，请求出相应的m的取值范围；若不能，请说明理由．
五、(第24题10分，第25题11分，共21分)
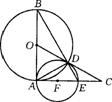
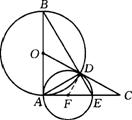
24.如图7，AB是⊙O的直径，过A作⊙O的切线，在切线上截取AC=AB，连结OC交⊙O于D，连结BD并延长交AC于E，⊙F是△ADE的外接圆，F在AE上．
求证：(1)CD是⊙F的切线；(2)CD=AE．
 |
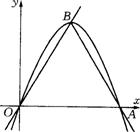
25.如图，抛物线y=-2x2+k与x轴的两个不同交点是O与A，顶点B在直线y=
x．
(1)求抛物线的解析式；
(2)证明△OAB是等边三角形；
(3)在抛物线上是否存在点P，使∠OPA=90° ?若存在，请求出点P的坐标；若不存在，请说明理由．
梅州市2005年中考数学模拟试题（一）参考答案
1．9． 2．2．6×10-5． 3．x≠3． 4．(-3，5)． 5．1440°．6．2/3(或2:3)． 7．5．
8．48π． 9．∠ADC=∠ACB或∠ACD=∠ABC或AC2=AD·AB等．10．n(n+1)-n=n2．
11．B 12．B 13．A 14．C． 15．C．
16．2．
17．-4．
18．过A作AE⊥BC于E，则四边形AECD是矩形．EC=AD=6，AE=CD=12，BE=BC=EC=5．
在Rt△ABE中，AB=13．则直角梯形ABCD的周长C=42(cm)．
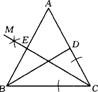19．(1)CM是所作的∠ACB的平分线(如图)；(2)∵∠ABC=∠ACB，又∠DBC=∠ABC/2，∠ECB=∠ACB/2，．∠DBC=∠ECB．又∵BC=BC，∴△DBC≌△EUB，∴BD=CE．
20．解得x1=-1，x2=-2．经检验，x1=-1，x2=-2都是原方程的根．
21．设过夜游客是x万人次，不过夜游客是y万人次．根据题意，得 x+y=500 1361x+172y=225400 解这个方程组，得x≈117 y≈383 答：过夜游客约是117万人次，不过夜游客约是38 3万人次．
22．过点P作PN⊥OM于N．在Rt△PON中，∵∠PON=27°，OP=800，PN=OP·sin∠PON=800 X sin 27°≈363(千米)．∵36 3千米>350千米，∴P市不在距台风中心35 O千米的范围内．答：P市不受到这次台风的影响．
23．(1)关于x的方程2x2+4x+m-1=O有两个非零实数根，∴△=16-8(m-1)≥O，且m-1≠O．∴m≤3且m≠l；
(2)设两个非零实数根是x1，x2，由根与系数的关系，得x1+x2=-2，x1·x2=(m-1)/2．如果x1，x2同为正数，即x1>0，x2>0，此时有x1+x2>O，这与x1+x2=-2矛盾，故此种情况不可能．如果x1，x2同为负数，即x1<0，x2<0，此时有x1+x2<0，且x1．x2>0．由x1．x2=(m--1)/2>O，解得m>1．此时m的取值范围是1<m≤3．
24．
(1)连结DF，∵OA=OD，FA=FD，∴∠OAD=∠ODA，∠FAD=∠FDA，∴∠BAC=∠FDO．AC为⊙O的切线，∴∠BAC=90°.∴∠FDO=9O。CD⊥DF．∴CD是O F的切线；
(2) ∵DF⊥CD∴Rt△CDF∽Rt△CAO∴DF/CD=OA/AC
又∵AC=AB=20A，∴DF/CD=OA/2OA=1/2 ．CD=2DF．∵AE=2DF．∴CD=AE．
25．（1）因为点B坐标是 (b/4，b2/8)，且点B在直线y=x上 b2=2b．点A与点O是两个不同的点，∴b≠0．∴b=2 抛物线的解析式是y=-2x2+2x；
(2)抛物线y=-2x2+2x与x轴的交点坐标是O(0，0)，A(，0)，顶点B(/2,3/2)．过B作BC⊥OA于C，则OC=/2，BC=3/2，AC=/2．BO=，AB=．OA=AB=BO=，∴△OAB是等边三角形；
(3)假设存在符合条件的点P(m，n)，依题意由图可知m>0，n>0，连结OP，PA，过点P作PD⊥OA 于D，则Rt△OPD∽Rt△PA D，．PD2=OD·DA，n2=m(-m)，2n2=-2m2+2m． ①
点P在抛物线y=-2x2+2x上，∴n=-2m2+2m． ② 由①和②解得n1=1/2或n2=0。(含去)．以n=1/2代入②，解得ml=
，m2=
．因此在抛物线y=-2x2+2x上存在点P，使得∠OPA=90°，其坐标是P(，
)或P(， )；