2006年浙江省杭州市各类高中招生考试
数学试题
考生须知:
1.本试卷分试题卷和答题卷两部分。满分120分,考试时间100分钟。
2.答题时,必须在答题卷密封区内写明校名、姓名和准考证号。
3.所有答案都必须做在答题卷标定的位置上,务必注意试题序号和答题序号相对应。
4.考试结束后,上交试题卷和答题卷。
试题卷
一.选择题(本题有15个小题,每小题3分,共45分)下面每小题给出的四个选项中,只有一个是正确的,请把正确选项前的字母填在答题卷中相应的格子内。
01.![]()
A、-2 B、0 C、1 D、2
02.要使式子![]() 有意义,字母x的取值必须满足
有意义,字母x的取值必须满足
A、x>![]() B、x≥
B、x≥![]() C、x>
C、x>![]() D、x≥
D、x≥![]()
03.![]() 是方程ax-y=3的解,则a的取值是
是方程ax-y=3的解,则a的取值是
A、5 B、-5 C、2 D、1
04.下列图形中,既是中心对称图形又是轴对称图形的是
A、等边三角形 B、菱形 C、等腰梯形 D、平行四边形
05.计算![]() 的结果是
的结果是
A、1 B、a C、a2 D、a10
 06.已知△ABC如右图,则下列4个三角形中,与△ABC相似的是
06.已知△ABC如右图,则下列4个三角形中,与△ABC相似的是
07.在某一场比赛前,教练预测:这场比赛我们队有50%的机会获胜。那么相比之下在下面4种情形的哪一种情形下,我们可以说这位教练说得比较准
A、该队真的赢了这场比赛 B、该队真的输了这场比赛
C、假如这场比赛可以重复进行10场而这个队赢了6场
D、假如这场比赛可以重复进行100场而这个队赢了51场
08.边长为4的正方形绕一条边旋转一周,所得几何体的侧面积等于
A、16 B、16π C、32π D、64π
09.已知y是x的一次函数,右表中列出了部分对应值,则m等于
| x | -1 | 0 | 1 |
| y | 1 | m | -1 |
A、-1 B、0 C、![]() D、2
D、2
10.如图,若圆心角∠ABC=100°,则圆周角∠ADC=
 A、80° B、100° C、130° D、180°
A、80° B、100° C、130° D、180°
 |
11.已知a与![]() 互为倒数,则满足条件的实数a的个数是
互为倒数,则满足条件的实数a的个数是
A、0 B、1 C、2 D、3
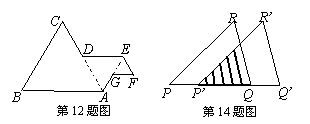
12.如图,△ABC、△ADE及△EFG都是等边三角形,D和G分别为AC和AE的中点。若AB=4时,则图形ABCDEFG外围的周长是
A、12 B、15 C、18 D、21
13.已知方程x2-6x+q=0可以配方成(x-p)2=7的形式,那么x2-6x+q=2可以配方成下列的
A、(x-p)2=5 B、(x-p)2=9 C、(x-p+2)2=9 D、(x-p+2)2=5
14.如图,把△PQR沿着PQ的方向平移到△P’Q’R’的位置,它们重叠部分的面积是△PQR面积的一半,若PQ=![]() ,则此三角形移动的距离PP’是
,则此三角形移动的距离PP’是
A、![]() B、
B、![]() C、1 D、
C、1 D、![]()
15.考虑下面4个命题:①有一个角是100°的两个等腰三角形相似;②斜边和周长对应相等的两个直角三角形全等;③对角线互相垂直且相等的四边形是正方形;④对角线相等的梯形是等腰梯形。其中正确命题的序号是
A、①②③④ B、①③④ C、①②④ D、②③④
二.填空题(本题有5个小题,每小题4分,共20分)
16.因式分解:(2x+1)2-x2= 。
 17.如图,北京奥运的5个吉祥物“福娃”都已放置在展桌上,其中“欢欢”和“贝贝”的位置已确定,则在另外三个位置中任取两个,其中有“迎迎”的概率为
。
17.如图,北京奥运的5个吉祥物“福娃”都已放置在展桌上,其中“欢欢”和“贝贝”的位置已确定,则在另外三个位置中任取两个,其中有“迎迎”的概率为
。
 | |||
 | |||
18.在正式运算中,任意两个一次二项式相乘后,将同类项合并得到的项数可以是 。
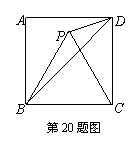
19.如图,在△ABC中, AB=12, AC=5,∠BAC=90°。若点P是BC的中点,则线段AP的长等于 ;若点P在直线BC上运动,设点B、C关于直线AP的对称点分别为B’、C’,则线段B’C’的长等于 。
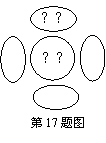
20.如图,已知正方形ABCD的边长为2,△BPC是等边三角形,则△CDP的面积是 ;△BPD的面积是 。
三.解答题(本题有6个小题,共55分)解答应写出文字说明、证明过程或推演步骤。
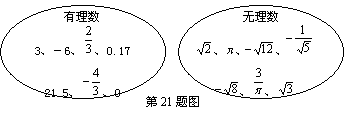
21.(本小题满分7分)在下面两个集合中各有一些实数,请你分别从中选出2个有理数和2个无理数,再用“+、-、×、÷”中的3种符合将选出的4个数进行3次运算,使得运算的结果是一个正整数。
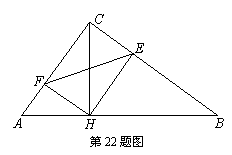 22.(本小题满分8分)如图,在Rt△ABC中,已知∠ACB=90°,且CH⊥AB、HE⊥BC、HF⊥AC。求证:
22.(本小题满分8分)如图,在Rt△ABC中,已知∠ACB=90°,且CH⊥AB、HE⊥BC、HF⊥AC。求证:
(1)△HEF≌△EHC;
(2)△HEF∽△HBC。
23.(本小题满分8分)已知![]() ,并且
,并且![]() 。请求出x的取值范围,并将这个范围在数轴上表示出来。
。请求出x的取值范围,并将这个范围在数轴上表示出来。
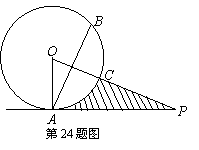 24.(本小题满分10分)如图,点P在圆O外,PA与圆O相切于A点,OP与圆周相交于C点,点B与点A关于直线PO对称,已知OA=4,PA=
24.(本小题满分10分)如图,点P在圆O外,PA与圆O相切于A点,OP与圆周相交于C点,点B与点A关于直线PO对称,已知OA=4,PA=![]() 。求:
。求:
(1)∠POA的度数;
(2)弦AB的长;
(3)阴影部分的面积。
25.(本小题满分10分)杭州休博会期间,嘉年华游乐场投资150万元引进一项大型游乐设施。若不计维修保养费用,预计开放后每月可创收33万元。而该游乐设施开放后,从第1个月到第x个月的维修保养费用累计为y(万元),且y=ax2+bx;若将创收扣除投资和维修保养费用称为游乐场的纯收益g(万元),g也是关于x的二次函数。
(1)若维修保养费用第1个月为2万元,第2个月为4万元。求y关于x的解析式;
(2)求纯收益g关于x的解析式;
(3)问设施开放几个月后,游乐场的纯收益达到最大?几个月后,能收回投资?
26.(本小题满分12分)已知,直线![]() 与x轴、y轴分别交于点A、B,以线段AB为直角边在第一象限内作等腰Rt△ABC,∠BAC=90°。且点P(1,a)为坐标系中的一个动点。
与x轴、y轴分别交于点A、B,以线段AB为直角边在第一象限内作等腰Rt△ABC,∠BAC=90°。且点P(1,a)为坐标系中的一个动点。
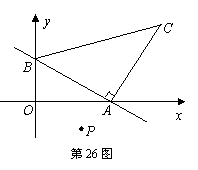 (1)求三角形ABC的面积
(1)求三角形ABC的面积![]()
(2)证明不论a取任何实数,三角形BOP的面积是一个常数;
(3)要使得△ABC和△ABP得面积相等,求实数a得值。
 2006年杭州市各类高中招生考试数学试题原卷:
2006年杭州市各类高中招生考试数学试题原卷:

说明
为了方便各位老师在今后的教学中使用本卷,本人由网上的扫描卷编辑了这份试卷,在此,首先对扫描卷的制作者表示感谢。
由于本人水平有限,编辑过程中难免出错,如有错落,请大家见谅并对照上面的扫描卷自行更正。
天门市卢家口中学 herewave
2006.07.22