浙江丽水市2005年初中毕业、升学考试试卷
 数 学
数 学
考生须知:
1、全卷满分为150分,考试时间为120分钟.
2、全卷分“卷一”和“卷二”两部分,其中“卷一”为选择题卷;“卷二”为非选择题卷.
3、答题前,请在答题卡上先填写姓名和准考证号,再用铅笔将准考证号和科目对应的括号或方框涂黑.
4、请在“卷二”密封区内填写座位号、县(市、区)学校、姓名和准考证号.
5、答题时,允许使用计算器.
卷一
说明:本卷有一大题,12小题,共48分.请用铅笔在答题卡上将所选选项的对应字母的方框涂黑、涂满.
一、细心选一选(本题有12小题,每小题4分,共48分.请选出各题中一个符合题意的正确选项,不选、多选、错选均不给分)
1.-2的绝对值是
(A)2
(B)-2 (C)![]() (D)-
(D)-![]()
2.tan45°的值是
(A)1
(B)![]() (C)
(C)![]() (D)
(D)![]()
3.据丽水气象台“天气预报”报道,今天的最低气温是17℃,最高气温是25℃,则今天气温t(℃)的范围是
(A)t<17 (B)t>25 (C)t=21 (D)17≤t≤25
4.把![]() 记作
记作
(A)n![]() (B)n+
(B)n+![]() (C)
(C)![]() (D)
(D)![]()
5.据丽水市统计局2005年公报,我市2004年人均生产总值约为10582元,则近似数10582的有效数字有
 (A)1个 (B)3个
(C) 4个
(D)5个
(A)1个 (B)3个
(C) 4个
(D)5个
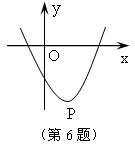
6.如图,抛物线的顶点P的坐标是(1,-3),
则此抛物线对应的二次函数有
(A)最大值1 (B)最小值-3
(C)最大值-3 (D)最小值1
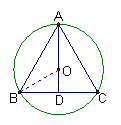
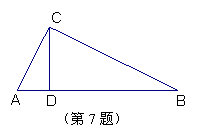 7.如图, 在Rt△ABC中, ∠ACB=90°,CD⊥AB于D,
7.如图, 在Rt△ABC中, ∠ACB=90°,CD⊥AB于D,
若AD=1,BD=4,则CD=
(A)2 (B)4
(C)![]() (D)3
(D)3
8.方程![]() 的解是
的解是
(A)![]() =2
(B)
=2
(B)![]() =4 (C)
=4 (C)![]() =-2 (D)
=-2 (D)![]() =0
=0
9.两圆的半径分别为3㎝和4㎝,圆心距为1㎝,则两圆的位置关系是
(A)外切 (B)内切 (C)相交 (D)外离
10.如图,将图中的阴影部分剪下来,围成一个几何体的侧面,使AB、DC重合,则所围成的几何体图形是
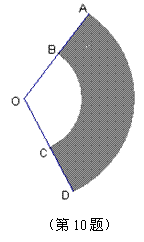 | |||
 | |||
(A) (B)

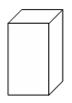
(C) (D)
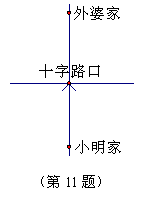 |
11.如图,小明周末到外婆家,走到十字路口处,记不清
前面哪条路通往外婆家,那么他能一次选对路的概率是
(A)![]() (B)
(B)![]()
(C)![]() (D)0
(D)0
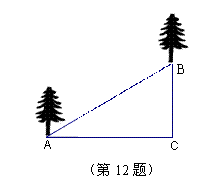
![]() 12.如图,在山坡上种树,已知∠A=30°,AC=3米,则相邻
12.如图,在山坡上种树,已知∠A=30°,AC=3米,则相邻
两株树的坡面距离AB=
(A)6米
(B)![]() 米
米
(C)2![]() 米
(D)2
米
(D)2![]() 米
米
浙江丽水市2005年初中毕业、升学考试试卷
数 学
卷 二
| 大题号 | 二 | 三 | 卷二总分 | ||||||
| 小题号 | 13~18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | |
| 得 分 | |||||||||
说明:本卷有二大题,13小题,共102分,请用蓝黑墨水的钢笔或圆珠笔直接在试卷上答题.
| 得分 | 评卷人 |
二、专心填一填(本题有6小题,每小题5分,共30分)
13.已知![]() ,则
,则![]() =
.
=
.
14.当![]() ≥0时,化简:
≥0时,化简:![]() =
.
=
.
15.因式分解:![]() 3-
3-![]() =
.
=
.
16.在平行四边形、矩形、菱形、正方形、等腰梯形的五种图形中,既是轴对称、又是中心对称的图形是 .
17.下列是三种化合物的结构式及分子式,请按其规律,写出后一种化合物的分子式 .
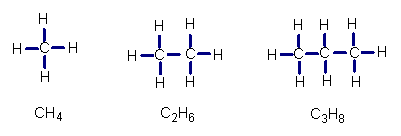
![]()

18.如图,ABCD是⊙O的内接四边形,AB是⊙O的直径,
过点D的切线交BA的延长线于点E,若∠ADE=25°,
|
三、耐心答一答(本题有7小题,共72分)以下各题必须写出解答过程.
| 得分 | 评卷人 |
19.(本题8分)
 选做题(请在下面给出的二个小题中选做一小题,若每小题都答,按得分高的给分)
选做题(请在下面给出的二个小题中选做一小题,若每小题都答,按得分高的给分)
(1)计算:(-2)0 +4×(-![]() ).
).
 (2)计算:2(x+1)-x.
(2)计算:2(x+1)-x.
20(本题8分)
已知关于x的一元二次方程x2-(k+1) x-6=0的一个根是2,
求方程的另一根和k的值.
| 得分 | 评卷人 |
21(本题8分)
如图,在⊙O中,弦AB与CD相交于点P,连结AC、DB.
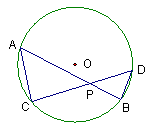 (1)求证:△PAC∽△PDB;
(1)求证:△PAC∽△PDB;
(2)当![]() 为何值时,
为何值时,![]() =4.
=4.
| 得分 | 评卷人 |
22、(本题10分)
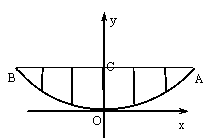
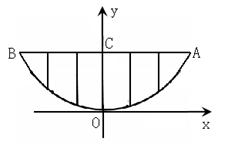 某校的围墙上端由一段段相同的凹曲拱形栅栏组成,如图所示,其拱形图形为抛物线的一部分,栅栏的跨径AB间,按相同的间距0.2米用5根立柱加固,拱高OC为0.6米.
某校的围墙上端由一段段相同的凹曲拱形栅栏组成,如图所示,其拱形图形为抛物线的一部分,栅栏的跨径AB间,按相同的间距0.2米用5根立柱加固,拱高OC为0.6米.
(1) 以O为原点,OC所在的直线为y轴建立平面直角坐标系,请根据以上的数据,求出抛物线y=ax2的解析式;
(2)计算一段栅栏所需立柱的总长度.(精确到0.1米)
| 得分 | 评卷人 |
23、(本题12分)
某公园有一个边长为4米的正三角形花坛,三角形的顶点A、B、C上各有一棵古树.现决定把原来的花坛扩建成一个圆形或平行四边形花坛,要求三棵古树不能移动,且三棵古树位于圆周上或平行四边形的顶点上.以下设计过程中画图工具不限.
(1)按圆形设计,利用图1画出你所设计的圆形花坛示意图;
(2)按平行四边形设计,利用图2画出你所设计的平行四边形花坛示意图;
(3)若想新建的花坛面积较大,选择以上哪一种方案合适?请说明理由.
 | |||
 | |||
|
|
| 得分 | 评卷人 |
24、(本题12分)
如图,AB是⊙O的直径,CB、CE分别切⊙O于点B、D,
 CE与BA的延长线交于点E,连结OC、OD.
CE与BA的延长线交于点E,连结OC、OD.
(1)求证:△OBC≌△ODC;
(2)已知DE=a,AE=b,BC=c,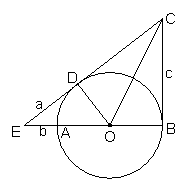 请你思考后,
请你思考后,
选用以上适当的数,设计出计算⊙O
半径r的一种方案:
①你选用的已知数是 ;
②写出求解过程.(结果用字母表示)
| 得 分 | 评卷人 |
25、(本题14分)
为宣传秀山丽水,在“丽水文化摄影节”前夕,丽水电
视台摄制组乘船往返于丽水(A)、青田(B)两码头,在
A、B间设立拍摄中心C,拍摄瓯江沿岸的景色.往返过程中,船在C、B处均不停留,离开码头A、B的距离s(千米)与航行的时间t(小时)之间的函数关系如图所示.根据图象提供的信息,解答下列问题:
(1)船只从码头A→B,航行的时间为 小时、航行的速度为 千米/时;船只从码头B→A,航行的时间为 小时、航行的速度为 千米/时;
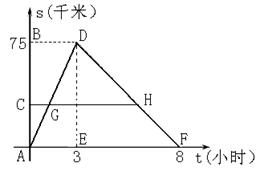 (2)过点C作CH∥t轴,分别交AD、DF于点G、H,设AC=
(2)过点C作CH∥t轴,分别交AD、DF于点G、H,设AC=![]() ,GH=y,求出y与
,GH=y,求出y与![]() 之间的函数关系式;
之间的函数关系式;
(3)若拍摄中心C设在离A码头25千米处, ![]() 摄制组在拍摄中心C分两组行动,一组乘橡皮艇漂流而下,另一组乘船到达码头B后,立即返回.
摄制组在拍摄中心C分两组行动,一组乘橡皮艇漂流而下,另一组乘船到达码头B后,立即返回.
①求船只往返C、B两处所用的时间;
②两组在途中相遇,求相遇时船只离拍摄中心C
有多远.
,
浙江丽水市2005年初中毕业、升学考试试卷
数学参考答案和评分标准
一、选择题(本题有12小题,每小题4分,共48分)
| 题次 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | A | A | D | C | D | B | A | B | B | D | B | C |
二、填空题(本题有6小题,每小题5分,共30分)
13.
![]() 14.
14.
![]() 15. x(x+1)(x-1)
15. x(x+1)(x-1)
16. 矩形、菱形、正方形 17. C4H10 18. 115
三、解答题(本题有6小题,共72分) 以下各题必须写出解答过程.
19、(本题8分)
(1)解:原式=1-2 …………………………………………………6分
=-1. …………………………………………………2分
(2)解:原式=2x+2-x ……………………………………………4分
= x+2. ………………………………………………4分
(若两小题都答,按得分高的题给分)
20、(本题8分)
解:设方程的另一根为x1,由韦达定理:2 x1=-6,
∴ x1=-3. …………………………………………………………4分
由韦达定理:-3+2= k+1,
∴k=-2. ……………………………………………………………4分
21、(本题8分)
(1)证明:∵∠A=∠D,∠C=∠B, …………………………………2分
∴△PAC∽△PDB; ………………………………………2分
(2)解:由(1)△PAC∽△PDB,得![]() =
=![]() , ………………2分
, ………………2分
 即
即![]() =4,∴
=4,∴![]() =2. …………………………………………2分
=2. …………………………………………2分
22、(本题10分)
解:(1) 由已知:OC=0.6,AC=0.6,
得点A的坐标为(0.6,0.6), ……2分
代入y=ax2,得a=![]() ,………………2分
,………………2分
∴抛物线的解析式为y=![]() x2.………1分
x2.………1分
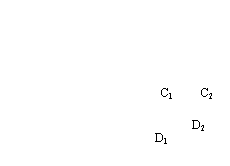
(2)点D1,D2的横坐标分别为0.2,0.4,…………………………1分
代入y=![]() x2,得点D1,D2的纵坐标分别为:
x2,得点D1,D2的纵坐标分别为:
y1=![]() ×0.22≈0.07,y2=
×0.22≈0.07,y2=![]() ×0.42≈0.27, ………………………………1分
×0.42≈0.27, ………………………………1分
∴立柱C1D1=0.6-0.07=0.53,C2D2=0.6-0.27=0.33, ……………2分
由于抛物线关于y轴对称,栅栏所需立柱的总长度为:
2(C1D1+ C2D2)+OC=2(0.53+0.33)+0.6≈2.3米. ……………1分
23、(本题12分)
解:(1)作图工具不限,只要点A、B、C在同一圆上;…………………4分
|
(3)∵r=OB=![]() =
=![]() ,………………………………1分
,………………………………1分
∴S⊙O=![]() r2=
r2=![]() ≈16.75, ……………………………1分
≈16.75, ……………………………1分
又S平行四边形=2S△ABC=2×![]() ×42×sin60º=8
×42×sin60º=8![]() ≈13.86,……1分
≈13.86,……1分
∵S⊙O > S平行四边形 ∴选择建圆形花坛面积较大. …………………1分
24、(本题12分)
(1)证明:∵CD、CB是⊙O的切线,∴∠ODC=∠OBC=90°, …………2分
OD=OB,OC= OC, ……………………………………………………1分
∴△OBC≌△ODC(HL); ………………………………………1分
(2)①选择a、b、c,或其中2个均给2分;
②若选择a、b:由切割线定理:a2=b(b+2r) ,得r=![]() .
.
若选择a、b、c:
方法一:在Rt△EBC中,由勾股定理:(b+2r)2+c2=(a+c)2,得r=![]() .
.
方法二:Rt△ODE∽Rt△CBE,![]() ,得r=
,得r=![]() .
.
方法三:连结AD,可证:AD//OC,![]() ,得r=
,得r=![]() .
.
若选择a、c:需综合运用以上的多种方法,得r=![]() .
.
若选择b、c,则有关系式2r3+br2-bc2=0.
(以上解法仅供参考,只要解法正确均给6分)
25.(本题14分)
解:(1)3、25;5、15;……………………………………………………4分
(2)解法一:设CH交DE于M,由题意:
ME=AC=x ,DM=75–x, … ……………………………………1分
∵GH//AF,△DGH∽△DAF , …………………………………1分
∴ ![]() ,即
,即![]() , ………………………………2分
, ………………………………2分
∴ y=8![]() . …………………………………………………1分
. …………………………………………………1分
解法二:由(1)知:A→B(顺流)速度为25千米/时,B→A(逆流)速度为15千米/时,y即为船往返C、B的时间.
y=![]() ,即y=8
,即y=8![]() .(此解法也相应给5分)
.(此解法也相应给5分)
(3)①当x=25时,y=8![]() (小时).……………………2分
(小时).……………………2分
②解法一:
|
|
|
|
|
a–b=15 b=5
船到B码头的时间t 1=![]() =2小时,此时橡皮艇漂流了10千米.
=2小时,此时橡皮艇漂流了10千米.
设船又过t2小时与漂流而下橡皮艇相遇,
则(5+15)t2=75–25–10,∴t2=2. ……………………………1分
∴船只离拍摄中心C距离S=(t 1+ t2)×5=20千米. …………1分
解法二:
设橡皮艇从拍摄中心C漂流至P处与船返回时相遇,
得![]() ,∴CP=20千米.
,∴CP=20千米.
(此解法也相应给3分)