初高中衔接型中考数学试题(3)及参考答案
1、(2001重庆)阅读下面材料:
在计算3+5+7+9+11+13+15+17+19+21时,我们发现,从第一个数开始,以后的每个数与它的前一个数的差都是一个相同的定值。具有这种规律的一列数,除了直接相加外,我们还可以用公式![]() 计算它们的和。(公式中的n表示数的个数,a表示第一个数的值,d表示这个相差的定值) 那么3+5+7+9+11+13+15+17+19+21=
计算它们的和。(公式中的n表示数的个数,a表示第一个数的值,d表示这个相差的定值) 那么3+5+7+9+11+13+15+17+19+21=![]()
用上面的知识解决下列问题:
为保护长江,减少水土流失,我市某县决定对原有的坡荒地进行退耕还林。从1995年起在坡荒地上植树造林,以后每年又以比上一年多植相同面积的树木改造坡荒地,由于每年因自然灾害、树木成活率、人为因素等的影响,都有相同数量的新坡荒地产生,下表为1995、1996、1997年的坡荒地面积和植树的面积的统计数据。假设坡荒地全部种上树后,不再水上流失形成新的坡荒地,问到哪一年,可以将全县所有的坡荒地全部种上树木。
| 1995年 | 1996年 | 1997年 | |
| 每年植树的面积(亩) | 1000 | 1400 | 1800 |
| 植树后坡荒地的实际面积(亩) | 25200 | 24000 | 22400 |
先阅读下面一段文字,然后再做后面的两个题目:
设![]() ①
①
则![]() ②
②
①+②得![]() 所以
所以![]()
(1)利用上述方法或结论证明:![]()
(2)若![]() ,求
,求![]() 。
。
2、(2003十堰)先阅读下面的材料,再解答下面的问题.
在平面直角坐标系中,有A(x1,y1)、B(x2,y2)两点,A、B两点间的距离用![]() 表示,则有:
表示,则有:![]() =
=![]() ,下面我们来证明这个公式:
,下面我们来证明这个公式:
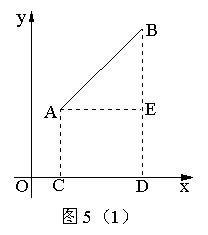
证明:如图5(1),过A点作x轴的垂线,垂足为C,则C点的横坐标为x1,过B点作x轴的垂线,垂足为D,则D点的横坐标为x2,过A点作BD的垂线,垂足为E,则E点的横坐标为x2,纵坐标为y1.
∴∣AE∣=∣CD∣=∣x1-x2∣
∣BE∣=∣BD∣-∣DE∣=∣y2-y1∣=∣y1-y2∣
在Rt△AEB中,由勾股定理得
∣AB∣2=∣AE∣2+∣BE∣2=∣x1-x2∣2+∣y1-y2∣2
∴![]() =
=![]() (因为∣AB∣表示线段长,为非负数)
(因为∣AB∣表示线段长,为非负数)
注:当A、B在其它象限时,同理可证上述公式成立.
(1) 在平面直角坐标系中有P(-1,2)、Q(2,-3)两点,求∣PQ∣;
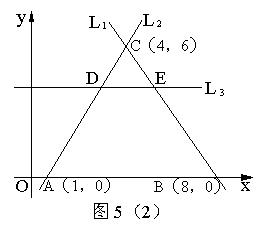
(2) 如图5(2),直线L1与L2相交于点C(4,6),L1、L2与x轴分别交于B、A两点,其坐标为B(8,0)、A(1,0),直线L3平行于x轴,与L1、L2分别相交于E、D两点,且∣DE∣=![]() ,求线段DA的长.
,求线段DA的长.
记两个函数的解析式分别为![]() 和
和![]() ,A与B为不同时为0且A+B≠0的两个实数,
称函数
,A与B为不同时为0且A+B≠0的两个实数,
称函数![]() 为由函数
为由函数![]() 与函数
与函数![]() 生成的函数。请举例说明由函数
生成的函数。请举例说明由函数![]() 与函数
与函数![]() 生成的函数
生成的函数![]() 与涵数
与涵数![]() 与函数
与函数![]() 之间一个关系。
之间一个关系。
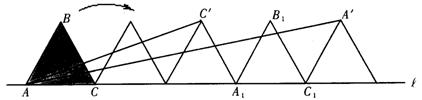
3、(2003金华)如图,已知边长为2的正三角形ABC沿着直线l滚动。(1)当△ABC滚动一周到△A1B1C1的位置,此时A点运动的路程为;约为;(精确到0.1,л=3.14…);(2)设△ABC滚动240°时,C点的位置为C’,△ABC滚动480°时,A点的位置为A’。请你利用三角函数中正切的两角和公式tan(α+β)=(tanα+ tanβ)÷(1-tanα·tanβ),求出∠CAC’+∠CAA’的度数。
初高中衔接型中考数学试题(3)及参考答案
1、解法一:从表中可知,1995年植树1000公顷,以后每年均比上一年多植树400公顷.1995年实有坡荒地25200公顷.种树1400公顷后,实有坡荒地只减少丁25200—24000=1200(公顷),因此,每年新产生的坡荒地为200公顷,即树木实际存活1200公顷.设从1996年起(1996年算第1年),n年全县的坡荒地全部植树,有1400n+![]() ×400—200n≥25200.即:n2+5n≥126.估算:当n=8时,82+5×8=104≤126.当n=9时,92+5×9=126.故到2004年,可将全县所有的坡荒地全部种上树木.
×400—200n≥25200.即:n2+5n≥126.估算:当n=8时,82+5×8=104≤126.当n=9时,92+5×9=126.故到2004年,可将全县所有的坡荒地全部种上树木.
解法二:从表中可知,1995年实有坡荒地25200公顷,1996年减少1200公顷,以后每年均比上一年多减少400公顷.设第n年的减少为0,则25200-(1200n+![]() ×400)≤0.即126-(n2+5n)≤0.当n=9时,126—8l-45=0.故到2004年可将全县所有的坡荒地全部种上树木.
×400)≤0.即126-(n2+5n)≤0.当n=9时,126—8l-45=0.故到2004年可将全县所有的坡荒地全部种上树木.
解法三:从表中可知:1996年荒地实际面积减少1200公顷,以后每年均比上一年多减少400公顷.
列表:
| 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 | 2004 |
| 1000 | 1400 | 1800 | 2200 | 2600 | 3000 | 3400 | 3800 | 4200 | 4600 |
| 25200 | 24000 | 22400 | 20400 | 18000 | 15200 | 12000 | 8400 | 4400 | 0 |
从表中可知,到2004年,可将全县所有的坡荒地全部种上树木.
(题29是一道新颖独特的阅读题,它的基本形式可归纳为:“阅读——理解——应用”,解题时应抓住三点:(1)读:读懂材料,读懂表格;(2)用:把阅读材料提供的结论正确地套用于解题中;(3)活:指解题时的计算,对n2+5n≥126这样的不等式,用估算法求年数n.)
2、解:(1)![]() =
=![]()
(2)∵直线L3平行于x轴 ∴DE:AB=CD:AC
而∣DE∣=![]() ,∣AC∣=
,∣AC∣=![]() ,∣AB∣=7
,∣AB∣=7
∴CD=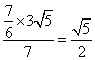 ,∴DA=AC一CD=
,∴DA=AC一CD=![]() 。线段DA的长是
。线段DA的长是![]() 。
。
3、