2005年河南省课改实验区中招试测试卷
数学
满分120分,考试时间:100分钟
一、选择题(每小题3分,共18分)
1、32的相反数是( )
A、-9 B、9 C、6 D、-6
2、2004年9月26日,中国西电东送北部通道骨干电源点之一的公伯峡水电站一号机组投产发电。至此,中国水电装机容量突破瓦,用科学记数法表示是( )瓦。
 A、1×109 B、1×1010 C、1×1011 D、1×1012
A、1×109 B、1×1010 C、1×1011 D、1×1012
 |  | ||||||
 | |||||||
3、 ……依次观察左边的三
个图形,并判断照此规律从左向右第四个图形是( )
 4、如图,图中的两个转盘分别被均匀地分成5个和4个扇形,每个扇形上都标有数字,同时自由转动两个转盘,转盘停止后,指针都落在奇数上的概率是( )
4、如图,图中的两个转盘分别被均匀地分成5个和4个扇形,每个扇形上都标有数字,同时自由转动两个转盘,转盘停止后,指针都落在奇数上的概率是( )
A、 B、 C、 D、
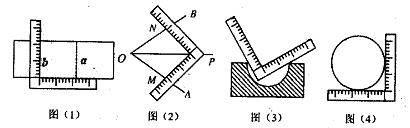
5、用一把带有刻度的直尺,①可以画出两条平行的直线a与b,如图⑴;②可以画出∠AOB的平分线OP,如图⑵所示;③可以检验工件的凹面是否为半圆,如图⑶所示;④可以量出一个圆的半径,如图⑷所示。这四种说法正确的是( )
A、1个 B、2个 C、3个 D、4个
 |
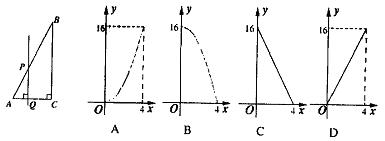
6、如图,Rt△ABC中,∠C=900,AC=4,BC=8,P是AB上一动点,直线PQ⊥AC于点Q,设AQ=x,则图中阴影部分的面积y与x之间的函数关系式的图象是( )
 |
二、填空题(每小题3分,共27分)
7、函数y=中,自变量x的取值范围是__________
8、对代数式4a作一个合理解释:____________________________________________________
9、要到玻璃店一块面积为1.21m2的正方形玻璃,那么该玻璃边长为________cm。
 10、已知:如图,AC⊥BC,BD⊥BC,AC>BC>BD,请你添加一个条件使△ABC∽△CDB,你添加的条件是___________________________。
10、已知:如图,AC⊥BC,BD⊥BC,AC>BC>BD,请你添加一个条件使△ABC∽△CDB,你添加的条件是___________________________。
11、已知圆锥的侧面展开图是半圆,那么这个圆锥的底面半径与母线的
比值是_________。
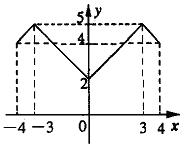
12、两个变量y与x之间的函数图象如图所示,则y的取值范围是__________
 13、双曲线y=和一次函数y=ax+b的图象的两个交点分别
13、双曲线y=和一次函数y=ax+b的图象的两个交点分别
是A(-1,-4),B(2,m),则a+2b=____________。
14、观察下列单项式:0、3x2、8x3、15x4、24x5、……,按
此规律写出第13个单项式是_________。
15、图⑴、图⑵是两种方法把6根圆形钢管用钢丝捆扎的截面
图。设图⑴、图⑵两种方法捆扎所需钢丝绳的长度是a、b(不记
接头部分),则a、b的大小关系为:a________b(填“<”、
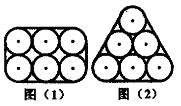 “=”或“>”)。
“=”或“>”)。
三、(第16、17小题各7分,第18小题8分,共22分)
16、已知x=+1,求x+1-的值。
17、下图反映了被调查用户对甲、乙两种品牌空调售后服务的满意程度(以下称:用户满意程度),分为很不满意、不满意、较满意、很满意四个等级,并依次记为1分、2分、3分、4分。
⑴、分别求甲、乙两种品牌用户满意程度分数的平均值(计算结果精确到0.01分);
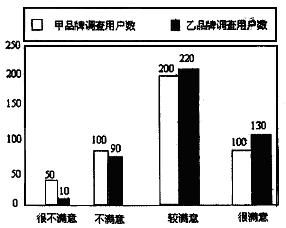 ⑵、根据条形统计图及上述计算结果说明哪个品牌用户满意程度较高?该品牌用户满意程度分数的众数是多少?
⑵、根据条形统计图及上述计算结果说明哪个品牌用户满意程度较高?该品牌用户满意程度分数的众数是多少?
 18、小明拿着一个罐子来找小华做游戏,罐子里有四个一样大小的玻璃球,两个黑色,两个白色。小明说:“使劲摇晃罐子,使罐子中的小球位置打乱,等小球落定后,如果是黑白相间地排列(如图所示),就算甲方赢,否则就算乙方赢。”他问小华要当甲方还是乙方,请你帮小华出主意,并说明理由。
18、小明拿着一个罐子来找小华做游戏,罐子里有四个一样大小的玻璃球,两个黑色,两个白色。小明说:“使劲摇晃罐子,使罐子中的小球位置打乱,等小球落定后,如果是黑白相间地排列(如图所示),就算甲方赢,否则就算乙方赢。”他问小华要当甲方还是乙方,请你帮小华出主意,并说明理由。
19、某商场购进甲、乙两种服装后,都加价40%标价出售。“春节”期间商场搞优惠促销,决定将甲、乙两种服装分别按标价的八折和九折出售。某顾客购买甲、乙两种服装共付款182元,两种服装标价之和为210元,问这两种服装的进价和标价各是多少元?
五、(每小题8分,共16分)
20、有一块梯形状的土地,现要平均分给两个农户种植(即将梯形的面积两等分),试设计两种方案(平分方案画在备用图上),并给予合理的解释。
 |  |
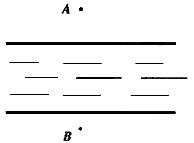 21、如图是一条河,点A为对岸一棵大树,点B是该岸一根标杆,且AB与河岸大致垂直,现有如下器材:一个卷尺,若干根标杆,根据所学的数学知识,设计出一个测量A、B两点间距离的方案,在图上画出图形,写出测量方法。
21、如图是一条河,点A为对岸一棵大树,点B是该岸一根标杆,且AB与河岸大致垂直,现有如下器材:一个卷尺,若干根标杆,根据所学的数学知识,设计出一个测量A、B两点间距离的方案,在图上画出图形,写出测量方法。
六、(每小题9分,共18分)
22、如图,在□ABCD中,点E、F在BD上,且BF=DE。
⑴、写出图中所有你认为全等的三角形;
 ⑵、延长AE交BC的延长线于G,延长CF交DA的延长线于H(请补全图形),证明四边形AGCH是平行四边形。
⑵、延长AE交BC的延长线于G,延长CF交DA的延长线于H(请补全图形),证明四边形AGCH是平行四边形。
23、已知:在Rt△ABC中,∠C=900,∠A、∠B、∠C的对边分别为a、b、c,设△ABC的面积为S,周长为l。
⑴、填表:
| 三边a、b、c | a+b-c |
|
| 3、4、5 | 2 | |
| 5、12、13 | 4 | |
| 8、15、17 | 6 |
⑵、如果a+b-c=m,观察上表猜想:=__________(用含有m的代数式表示)。
⑶、证明⑵中的结论。
七、(11分)
24、如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,AB=2,DC=2,点P在边BC上运动(与B、C不重合),设PC=x,四边形ABPD的面积为y。
⑴、求y关于x的函数关系式,并写出自变量x的取值范围;
 ⑵若以D为圆心、为半径作⊙D,以P为圆心、以PC的长为半径作⊙P,当x为何值时,⊙D与⊙P相切?并求出这两圆相切时四边形ABPD的面积。
⑵若以D为圆心、为半径作⊙D,以P为圆心、以PC的长为半径作⊙P,当x为何值时,⊙D与⊙P相切?并求出这两圆相切时四边形ABPD的面积。
2005年河南省课改实验区中招试测试题答案及评分标准
数学
说明:
1、本参考答案中每题只提供了一种解法,如果考生的解答与提供的解法不同,可根据提供的解法的评分标准精神进行评分。
2、评阅试卷,要坚持每题评阅到底,不能因考生解答中出现错误而中断对本题的评阅。如果考生的解答在某一步出现错误,影响后继部分而未改变本题的内容和难度,视影响的程度决定对后面给分多少 ,但原则上不超过后继部分应得分数之半;如果有严重概念性错误,就不给分。
一、选择题(每小题3分,共18分)
1、A 2、C 3、D 4、B 5、D 6、A
二、填空题(每小题3分,共27分)
7、x≥-7; 8、正确合理即可; 9、1.1
10、∠CAB=∠BCD或∠CBA=∠BDC或BC2=AC·BD等;
11、1∶2 12、2≤y≤5 13、-2 14、168x13 15、=
三、(第16、17小题各7分,第18小题8分,共22分)
16、解:原式=.
当x=+1时,原式=-………………………………………………… 7分
17、解:⑴、甲品牌被调查用户数为:50+100+200+100=450(户)
乙品牌被调查用户数为:10+90+220+130=450(户)
甲品牌满意程度分数的平均值=≈2.78分
乙品牌满意程度分数的平均值=≈3.04分
答:甲、乙品牌满意程度分数的平均值分别是2.78分、3.04分。……………………… 1分
⑵、用户满意程度较高的品牌是乙品牌。
因为乙品牌满意程度分数的平均值较大,且由统计图知,乙品牌“较满意”、“很满意”的用户数较多;该品牌用户满意程度的众数是3分。………………………………………… 3分
18、解:小华当乙方。理由:设A1表示第一个黑球,A2表示第二个黑球,B1表示第一个白球,B2表示第二个白球。有24种可能结果(可以利用树状图或表格解释),黑白相间排列的有8种。因此,甲方赢的概率为,乙方赢的概率为,故小华当乙方。…………… 8分
四、(8分)
19、解:设甲种服装的标价是x元,则进价是元;乙种服装的标价是y元,则进价是元。…………………………………………………………………………………………… 2分
依题意,得:…………………………………………………………… 5分
解之,得:………………………………………………………………………… 7分
=50(元),=100(元)……………………………………………………… 8分
五、(每小题8分,共16分)
20、只要正确、合理即可,以下三种方案供参考。写出一种方案给4分,满分8分。
解:设梯形上、下底分别为a、b,高为h。
方案一:如图1,连结梯形上、下底的中点E、F,则S四边形ABFE=S四边形EFCD=
方案二:如图2,分别量出梯形上、下底a、b的长,在下底BC上截取BE=(a+b),连接AE,则S△ABE=S四边形AECD=。
方案三:如图3,连结AC,取AC的中点E,连结BE、ED,则图中阴影部分的面积等于梯形ABCD的面积的一半。
分析此方案可知,∵AE=EC,∴S△AEB=S△EBC,S△AED=S△ECD,
∴S△AEB+S△AED=S△EBC+S△ECD,
 ∴图中阴影部分的面积等于梯形ABCD的面积的一半
∴图中阴影部分的面积等于梯形ABCD的面积的一半
 |  | ||
21、测量A、B两点间距离的方法有很多种,答案不惟一,一般采用全等、相似的知识来解决,只要答案合理、正确均给分。
六、(每小题9分,共18分)
22、⑴、△ABE≌△CDF,△AED≌△CFB,△ABD≌△CDB;………………………… 3分
⑵、∵BF=DE,∴BF+FE=DE+FE,即BE=DE。
∵四边形ABCD是平行四边形,∴AB∥CD。
 ∴∠ABD=∠CDB。
∴∠ABD=∠CDB。
在△ABE和△CDF中:
∴△ABE≌△CDF,
∴∠AEB=∠CFD,
∴HC∥CG,∴四边形AGCH为平行四边形。…………………………………………… 3分
23、⑴填表:
| 三边a、b、c | a+b-c |
|
| 3、4、5 | 2 | |
| 5、12、13 | 4 | 1 |
| 8、15、17 | 6 |
…………………………………………… 3分
⑵、=……………………………………………………………………………………… 3分
⑶、证明:∵a+b-c=m,∴a+b=m+c,
∴a2+2ab+b2=m2+c2+2mc。
∵a2+b2=c2,∴2ab=m2+2mc
∴m(m+2c)
∴==……………………………………………………………… 9分
七、(11分)
24、⑴过点D作DE⊥BC于E,
∵∠ABC=900,∴DE=AB=2,
又∵DC=2,∴EC==2
∴BC=BE+EC=AD+EC=2+1=3
∴S四边形ABPD==4-x,
即 y=-x+4 (0<x<3)……………………………………………………………… 4分
⑵当P与E重合时,⊙P与⊙D相交,不合题意;
当点P与点E不重合时,在Rt△DEP中,
DP2=DE2+EP2=22+2-x2=x2-4x+8
∵⊙P的半径为x,⊙D的半径为,
∴①当⊙P与⊙D外切时,
(x+)2=x2-4x+8,解得 x=
此时四边形ABPD的面积y=4-=………………………………………………… 8分
②当⊙P与⊙D内切时,
(x+)2=x2-4x+8,解得 x=
此时四边形ABPD的面积y=4-=
∴⊙P与⊙D相切时,四边形ABPD的面积为或…………………………………… 11分