1、(2005年安徽)某射击运动爱好者在一次比赛中共射击10次,前6次射击共中53环(环数均是整数),如果他想取得不低于89环的成绩,第7次射击不能少于__6___环.
2、（2005年北京）
不等式组
的解集是____
________。
3、（长沙市 2005）不等式组
的解集为C
A．
B．
C．
D．无解
4、（2005常州市）七（２）班共有50名学生，老师安排每人制作一件
型或
型的陶艺品，学校现有甲种制作材料36
，乙种制作材料29，制作、两种型号的陶艺品用料情况如下表：
| 需甲种材料 | 需乙种材料 | |
| 1件 | ０.9 | 0.3 |
| 1件 | 0.4 | 1 |
（1）设制作型陶艺品
件，求的取值范围；
（2）请你根据学校现有材料，分别写出七（2）班制作型和型陶艺品的件数．
解：（1）由题意得：
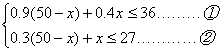2分
由①得，x≥18，由②得，x≤20，
所以x的取值得范围是18≤x≤20（x为正整数） 4分
（2）制作A型和B型陶艺品的件数为：
①制作A型陶艺品32件，制作B型陶艺品18件； 5分
②制作A型陶艺品31件，制作B型陶艺品19件； 6分
③制作A型陶艺品30件，制作B型陶艺品20件；
5、（2005年梅州市）为节约用电，某学校于本学期初制定了详细的用电计划。如果实际每天比计划多用2度电，那么本学期的用电量将会超过2530度；如果实际每天比计划节约2度电，那么本学期用电量将会不超过2200度电。若本学期的在校时间按110天计算，那么学校每天用电量应控制在什么范围内？
解：设学校每天用电量为x度，依题意可得：
解得：
，即学校每天用电量应控制在21度～22度范围内。
6、（2005年龙岩市）煤炭是龙岩市的主要矿产资源之一，每天有大量的煤炭运往外地．某煤矿现有100吨煤炭要运往甲、乙两厂．通过了解获得甲、乙两厂的有关信息如下表：（表中运费栏“元/t·km” 表示每吨煤炭运送二千米所需人民币）
| 厂别 | 运费(元/t·km) | 路程(km) | 所需的吨数(t) |
| 甲厂 | 1 | 150 | 不超过60 |
| 乙厂 | 1.2 | 100 | 不超过80 |
要把100吨煤全部运出，试写出总运费y（元）与运往甲厂x（吨）煤炭之间的函数关系式；如果你是该矿的矿主，请设计出合理的运送方案，使所需的总运费最低，并求出最低的总运费．
7、(2005年漳州)某公司有员工50人，为了提高经济效益，决定引进一条新的生产线并从现有员工中抽调一部分员工到新的生产线上工作，经调查发现：分工后，留在原生产线上工作的员工每月人均产值提高40％；到新生产线上工作的员工每月人均产值为原来的3倍，设抽调x人到新生产线上工作.
⑴填空：若分工前员工每月的人均产值为a元，则分工后，留在原生产线上工作的员工每月人均产值是 元，每月的总产值是 元；到新生产线上工作的员工每月人均产值是 元，每月的总产值是 元；
⑵分工后，若留在原生产线上的员工每月生产的总产值不少于分工前原生产线每月生产的总产值；而且新生产线每月生产的总产值又不少于分工前生产线每月生产的总产值的一半。问：抽调的人数应该在什么范围？
解：（1）填空：（1＋40％）a，（50－x）（1＋40％）a， 3a ，3ax.
（2）由题可得不等式组：
（其中a＞0）
解得x的取值范围为：
由于x只能取正整数，所以抽调的人数应在9－14人之间（包括9人和14人）
8、（2005年临沂市）关于x的不等式3x―2a≤―2的解集如图所示，则a的值是 
。
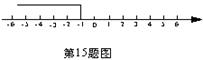
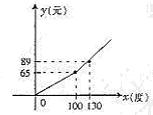
9、 （2005广东省）今年以来，广东大部分地区的电力紧缺，电力公司为鼓励市民节约用电，采取按月用电量分段收费办法，若某户居民每月应交电费y（元）与用电量x（度）的函数图象是一条折线（如图所示），根据图象解下列问题：
（1）分别写出当0≤x≤100和x≥100时，y与x的函数关系式；
（2）利用函数关系式，说明电力公司采取的收费标准；
（3）若该用户某月用电62度，则应缴费多少元？若该用户某月缴费105元时，则该用户该月用了多少度电？
10、（浙江省2005）一个矩形，两边长分别为xcm和10cm，如果它的周长小于80cm，面积大于100cm2．求x的取值范围．
解：矩形的周长是2(x+10)cm，面积是10xcm2
根据题意，得
解这个不等式组，得
所以x的取值范围是10＜x＜30．
11、（2005年南安调研）南泉汽车租赁公司共有30辆出租汽车,其中甲型汽车20辆,乙型汽车10辆。现将这30辆汽车租赁给A、B两地的旅游公司，其中20辆派往A地，10辆派往B地，两地旅游公司与汽车租赁公司商定每天价格如下表：
| 每辆甲型车租金（元/天） | 每辆乙型车租金（元/天） | |
| A地 | 1000 | 800 |
| B地 | 900 | 600 |
(1)
设派往A地的乙型汽车辆，租赁公司这30辆汽车一天共获得的租金为
（元），求与之间的函数解析式，并写出自变量的取值范围；
（2）若要使租赁公司这30辆汽车一天所获得的租金总额不低于26800元，请你说明有多少种分派方案，并将各种方案设计出来；
（3）如果要使这30辆汽车每天获得的租金最多，请你为租赁公司提出合理的分派方案．
解：（1）
（2）依题意得：
，又因为
∴
，因为是整数
∴=8，9，10，方案有3种
方案1：A地派甲型车12辆，乙型车8辆；B地派甲型车8辆，乙型车2辆；
方案2：A地派甲型车11辆，乙型车9辆；B地派甲型车9辆，乙型车1辆；
方案3：A地派甲型车10辆，乙型车10辆；B地派甲型车10辆。
（3）∵
是一次函数，且
﹥0，
∴随的增大而增大，
∴当=10时，这30辆车每天获得的租金最多，
∴合理的分配方案是A地派甲型车10辆，乙型车10辆；B地派甲型车10辆。
12、（湖州市2005）某高速公路收费站，有m（m>0）辆汽车排队等候收费通过。假设通过收费站的车流量（每分钟通过的汽车数量）保持不变，每个收费窗口的收费检票的速度也是不变的。若开放一个收费窗口，则需20分钟才可能将原来排队等候的汽车以及后来接上来的汽车全部收费通过；若同时开放两个收费窗口，则只需8分钟也可将原来排队等候的汽车以及后来接上来的汽车全部收费通过。若要求在3分钟内将排队等候收费的汽车全部通过，并使后来到站的汽车也随到随时收费通过，请问至少要同时开放几个收费窗口？
13、(2005年潍坊)为了加强学生的交通安全意识，某中学和交警大队联合举行了“我当一日小交警”活动，星期天选派部分学生到交通路口值勤，协助交通警察维护交通秩序．若每一个路口安排4人，那么还剩下78人；若每个路口安排8人，那么最后一个路口不足8人，但不少于4人．求这个中学共选派值勤学生多少人？共有多少个交通路口安排值勤？
解:设这个学校选派值勤学生人,共到个交通路口值勤. …………………
根据题意得:
将方程(1)代入不等式(2), 
，
整理得:19.5<
，
根据题意取20,这时为158．
14、(2005年南通)海门市三星镇的叠石桥国际家纺城是全国最大的家纺专业市场，年销售额突破百亿元．2005年5月20日，该家纺城的羽绒被和羊毛被这两种产品的销售价如下表：
| 品 名 | 规格（米） | 销售价（元/条） |
| 羽绒被 | 2×2.3 | 415 |
| 羊毛被 | 2×2.3 | 150 |
现购买这两种产品共80条，付款总额不超过2万元．问最多可购买羽绒被多少条?
解：设购买羽绒被x条，则购买羊毛被(80－x)条，
根据题意，得 415x＋150(80－x)≤20000．整理，得 265x≤8000．解之，得 x≤
．∵x为整数，∴x的最大整数值为30．
15、(2005年包头) 小明计划将今年春节期间得到的压岁钱的一部分作为自己一年内购买课外书籍的费用，其余的钱计划买些玩具去看望市福利院的孩子们。某周日小明在商店选中了一种小熊玩具，单价是10元，按原计划买了若干个，结果他的压岁钱还余30％，于是小明又多买了6个小熊玩具，这样余下的钱仅是压岁钱的10％。
(1)问小明原计划买几个小熊玩具，小明的压岁钱共有多少元；(6分)
(2)为了保证小明购书费用不少于压岁钱的20％，问小明最多可比原计划多买几个小熊玩具。(6分)
16、（乌鲁木齐2005）一本科普读物共98页，王力读了一周（7天）还没有读完。而张勇不到要周就读完了。张勇平均每天比王力多读3页，王力平均每天读多少页（答案取整数）？
解：设王力每天平均读x页，则张勇平均每天读（x＋3）页
据题意得：
解不等式（1）得x＜14
解不等式（2）得x＞11因此不等式组的解集是11＜x＜14
∵x取整数
∴x＝12或x＝13
17、（2005年杭州）宏志高中高一年级近几年来招生人数逐年增加,去年达到550名,其中面向全省招收的“宏志班”学生,也有一般普通班学生.由于场地、师资等限制,今年招生最多比去年增加100人,其中普通班学生可多招20%,“宏志班”学生可多招10%,问今年最少可招收”宏志班”学生多少名?
最少110人
18、（2005福州）百舸竞渡，激情飞扬。端午节期间，某地举行龙舟比赛。甲、乙两支龙舟队在比赛时路程y（米）与时间x（分钟）之间的函数图象如图所示。根据图象回答下列问题：
（1）1.8分钟时，哪支龙舟队处于领先位置？
（2）在这次龙舟赛中，哪支龙舟队先到达终点？先到达多少时间？
（3）求乙队加速后，路程y（米）与时间x（分钟）之间的函数关系式。
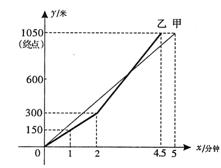
解：（1）1.8分钟时，甲龙舟队处于领先位置；
（2）这次龙舟笑中，乙龙舟队先到达终点，先到0.5分钟；
（3）
19、（连云港市2005）光明农场现有某种植物10 000kg，打算全部用于生产高科技药品和保健食品．若生产高科技药品，1kg该植物可提炼出0.01kg的高科技药品，将产生污染物0.1kg；若生产保健食品，1kg该植物可制成0.2kg的保健食品，同时产生污染物0.04kg．已知每生产1kg高科技药品可获利润5 000元，每生产1kg保健食品可获利润100元．要使总利润不低于410 000元，所产生的污染物总量不超过880kg，求用于生产高科技药品的该植物重量的范围．
解：设用于生产高科技药品的该植物重量为xkg，则用于生产保健食品的植物重量为
kg.
根据题意，得 
解得 7000≤
≤8000．
20、（厦门2005） 某软件公司开发出一种图书管理软件，前期投入的开发、广告宣传费用共50000元，且每售出一套软件，软件公司还需支付安装调试费用200元.
（1）试写出总费用y(元)与销售套数x(套)之间的函数关系式；
（2）如果每套定价700元，软件公司至少要售出多少套软件才能确保不亏本？
(1) 解：y＝50000＋200x …… 4分
(2) 解1：设软件公司至少要售出x套软件才能确保不亏本，则有：
700 x≥50000＋200x …… 7分
解得：x≥100 …… 9分
答：软件公司至少要售出100套软件才能确保不亏本. …… 10分
解2：每套成本是＋200 …… 5分
若每套成本和销售价相等则：700＝＋200 …… 7分
解得：1＝ ∴ x＝100 …… 9分
答：软件公司至少要售100套软件才能确保不亏本. …… 10分
解3：每套成本是＋200 …… 5分
由题意得：700≥＋200 …… 7分
解得：1≥ ∴ x≥100
21、（2005南充）某钢铁企业为了适应市场竞争的需要，提高生产效率，决定将一部分钢铁生产一线员工调整去从事服务性工作．该企业现有钢铁生产一线员工1000人，平均每人全年可创造钢铁产品产值30万元．根据规划，调整出去一部分一线员工后，生产一线员工平均每人全年创造钢铁产品产值可增加30％，调整到服务性工作岗位人员平均每人全年可创造产值24万元．如果要保证员工岗位调整后，它们全年的总产值至少增加20%，并且钢铁产品的产值不能超过33150万元．怎样安排调整到服务性工作岗位的人数？
解：设从现有钢铁生产一线员工中调整x人从事服务性工作． …………（1分）
根据题意，建立不等式组：
……………（5分）
解不等式1，得x≤200．
解不等式2，得x≥150． ……………………（7分）
即不等式组的解集是 150≤x≤200．
答：安排调整到服务性工作岗位的人数不低于150人，不超过200人．
22、(绵阳2005)如果关于x的不等式 (a+1) x>a+1的解集为x<1，那么a的取值范围是D
A. a>0 B. a<0 C. a>-1 D. a<-1
23、
(黄石市2005)已知关于x的不等式2x+m>-5的解集如图所示，则m的值为( A )
A．1 B．0
C．-1 D．-2
24、（镇江市2004） 修建润扬大桥，途经镇江某地，需搬迁一批农户，为了节约土地资源和保护环境，政府决定统一规划建房小区，并且投资一部分资金用于小区建设和补偿到政府规划小区建房的搬迁农户.建房小区除建房占地外，其余部分政府每平方米投资100元进行小区建设；搬迁农户在建房小区建房，每户占地100 平方米，政府每户补偿4万元，此项政策，吸引了搬迁农户到政府规划小区建房，这时建房占地面积占政府规划小区总面积的20%.
政府又鼓励非搬迁户到规划小区建房，每户建房占地120平方米，但每户需向政府交纳土地使用费2.8万元，这样又有20户非搬迁户申请加入.此项政策，政府不但可以收取土地使用费，同时还可以增加小区建房占地面积，从而减少小区建设的投资费用.若这20户非搬迁户到政府规划小区建房后，此时建房占地面积占政府规划规划小区总面积的40%.
（1）设到政府规划小区建房的搬迁农户为x户，政府规划小区总面积为y平方米.
可得方程组 解得
（2）在20户非搬迁户加入建房前，请测算政府共需投资 __________万元
在20户非搬迁户加入建房后，请测算政府将收取的土地使用费投入后，还需投资
__________万元.
（3）设非搬迁户申请加入建房并被政府批准的有z户，政府将收取的土地使用费投入
后，还需投资p万元.
①求p与z的函数关系式.
②当p不高于140万元，而又使建房占地面积不超过规划小区总面积的35%时，
那么政府可以批准多少户非搬迁户加入建房？
（1）
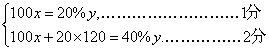
（2）192…………………………………5分
112…………………………………6分
（3）①
………………………………7分
②由题意得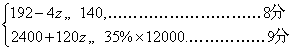
解得
∴政府可批准13、14或15户非搬迁户加入建房.
25、（淄博市2004）我市一山区学校为部分家远的学生安排住宿，将部分教室改造成若干间住房. 如果每间住5人，那么有12人安排不下；如果每间住8人，那么有一间房还余一些床位，问该校可能有几间住房可以安排学生住宿？住宿的学生可能有多少人？
解：设有x间住房，有y名学生住宿.
根据题意，得
……………………3分
把①代入②，得
0
8x-5x-128
解得 
. ……………………………………………………… 5分
因为x为整数，所以x可取5，6, …………………………………………6分
把x的值代入①，得y的值为37，42. ………………………………… 7分
| |
26、（2004年新疆）用若干辆载重量为8吨的汽车运一批货物，若每辆汽车只装5吨，则剩下10吨货物，若每辆车装满8吨，则最后一辆汽车不空也不满，请问有多少辆汽车？
设有x辆汽车
则
解之得：1
2 
∴不等式组解集为
∴满足不等式组解集的整数解为4或5
27、（盐城市2004）分别解不等式
和
，再根据它们的解集写出x与y的大小关系.
．解：不等式的解集为
；不等式的解集为
.
27、（2004年湖北省襄樊）襄樊市认真落实国家关于减轻农民负担，增加农民收入的政策，从2003年开始减征农业税，2002年至2004年征收农业税变化情况见表（1），2004年市政府为了鼓励农民多种粮食，实行保护价收购，并对种植优质水稻（如中籼稻）另给予每亩15元的补贴（摘自《襄樊日报》2004年5月5日消息）.我市农民李江家有4个劳动力，承包20亩土地，今年春季全部种植中籼稻和棉花，种植中籼稻和棉花每亩所需劳力和预计每亩平均产值见表（2）.设2004年李江家种植中籼稻和棉花的预计总收入为P元，种植中籼稻的土地为亩.
|
| 年份 | 2002 | 2003 | 2004 |
| 农业税（元/亩） | 117.24 | 70.44 | 38.26 |
|
| 农作物 | 产值（元/亩） | 劳力（人/亩） |
| 中籼稻 | 785 | 0.15 |
| 棉花 | 1200 | 0.35 |
（1） 李江家从国家开始减征农业税后两年可少交农业税多少元？
（2）
若不考虑上缴农业税，请写出P（元）与（亩）的函数关系式.
（3） 李江家在不考虑他人帮工等其它因素的前提下，怎样安排中籼稻和棉花的种植面积才能保证P最大？最大值是多少？
解：(1)由表(1)可得
=2515.6(元).
答：李江家从国家开始减征农业税后两年可少交农业税2515.6元.
(2)
(3)由题意，可得
解之，得
由于-400＜0，所以P随的减小而增大.
所以，当=15时，
（元）.
∴
（亩）.
28、（无为县2004） 某城市平均每天产生生活垃圾700吨，由甲、乙两个垃圾处理厂处理.已知甲厂每时可处理垃圾55吨，需费用550元；乙厂每时可处理垃圾45吨，需费用495元.（1）甲、乙两厂同时处理该城市的生活垃圾，每天需多长时间才能处理完？（2）如果规定该城市每天用于处理生活垃圾的费用不超过7260元，那么甲厂每天至少应处理垃圾多长时间？
解：（1）设每天需x小时才能处理完垃圾，由题意，得
(22+45) x=700, ∴ x=7
答：每天需7小时才能处理完垃圾
（2）设甲厂每天至少处理x小时，乙厂每天处理垃圾y小时，
则
解得：x≥8
答：甲厂每天至少处理垃圾8小时
29、
（2004年无锡）设“○”、“□”、“△”分别表示三种不同的物体，用天平比较它们质量的大小，两次情况如图所示，那么每个“○”、“□”、“△”这样的物体，按质量从小到大的顺序排列为（ D ）
A、○□△ B、○△□ C、□○△ D、△□○
30、（2004年芜湖）如果t>0,那么a+t与a的大小关系是 ( A ).
A.a+t>a B.a+t<a C.a+t≥a D.不能确定
31、（泰州2004）小芳和爸爸、妈妈三人玩跷跷板,三人的体重一共为150千克,爸爸坐在跷跷板的一端；体重只有妈妈一半的小芳和妈妈一同坐在跷跷板的另一端.这时,爸爸的那一端仍然着地.请你猜一猜小芳的体重应小于 D
A. 49千克 B. 50千克 C. 24千克 D. 25千克
※※※32、（安徽理科实验班2004）若方程组
的解为
且
＜3，则
的取
值范围是 －1＜＜5
．
33、（2004年苏州）某中学为筹备校庆活动，准备印制一批校庆纪念册。该纪念册每册需要10张8K大小的纸，其中4张为彩页，6张为黑白页。印制该纪念册的总费用由制版费和印刷费两部分组成，制版费与印数无关，价格为：彩页300元/张，黑白页50元/张；印刷费与印数的关系见下表。
| 印数a (单位：千册) | 1≤a＜5 | 5≤a＜10 |
| 彩色 (单位：元/张) | 2．2 | 2．0 |
| 黑白（单位：元/张） | 0．7 | 0．6 |
（1）印制这批纪念册的制版费为 元；
（2）若印制2千册，则共需多少费用？
（3）如果该校希望印数至少为4千册，总费用至多为60 000元，求印数的取值范围。（精确到0。01千册）
解：（１）１ ５００（元） （２）若印制2千册，则印刷费为：（２.2×4+0.7×6）×2 000=26 000 (元)
∴总费用为：26 000+1 500=27 500 (元）
(3)设印数为x千册，
①若4≤x＜5，由题意，得
1 000 ×(2.2×4+0.7×6) x+1 500≤60 000
解得x≤4。5 （１分）
∴4≤x≤４。5
②若x≥５，由题意，得
1 000×(2.0×4+0.6×6) x+1500≤60 000
解得x≤5。
∴5≤x≤5。
综上所述，符合要求的印数x（千册）的取值范围为：
4≤x≤４。5 或 5≤x≤5。
34、（陕西省2004）如图，若数轴上的两点A、B表示的数分别为a、b，则下列结论正确的是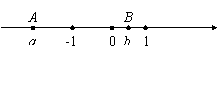【 A 】
A．
b-a>0
B．a-b>0
C．2a+b>0 D．a+b>0
35、（连云港市2004）据统计，连云港港口2002年、2003年的内外贸吞吐总量分别为3300万吨和3760万吨，其中2003年外贸和内贸吞吐量分别较2002年增长10%和20%．
（1）试确定2002年的外贸和内贸吞吐量；
（2）2004年港口内外贸吞吐量的目标是：总量不低于4200万吨，其中外贸吞吐量所占比重不低于60%．预计2004年的内贸吞吐量较2003年增长10%，则为完成上述目标，2004年的外贸吞吐量较2003年至少应增加多少万吨？
解：（1）设2002年内贸、外贸吞吐量分别为x和y万吨，
则
……………………（2分）
解得
，
答：2002年内贸、外贸吞吐量分别为1300万吨和2000万吨．……………………（4分）
（2）设2004年较2003年外贸吞吐量增加ｚ万吨．
又2003年内贸吞吐量为1300×(1+20%) =1560(万吨),
2003年外贸吞吐量为3760
(万吨).
则
……………………（6分）
解得
．
答：2004外贸吞吐量较2003年至少应增加374万吨
36、（2004年龙岩）为加强公民节约用水，减少污水排放的环保意识，某城市制定了以下用水收费标准（含城市污水处理费）：每户每月用水未超过8 m3时，按1.2元/ m3收费；每户每月用水超过8 m3时，其中的8 m3仍按原标准收费，超过部分按1.9元/m3收费.设某户每月用水量为x(m3)，应交水费为y(元).
（1）分别写出用水未超过8m3和超过8m3时，y与x之间的函数关系式；
（1） 某用户五月份共交水费13.4元，问该用户五月份用水多少m3.
解：（1）当x≤8时，y=1.2x……………………………………（3分）
当x>8时，y=1.9x-5.6…………………………………（6分）
（写成y=8×1.2+(x-8)×1.9，不扣分）
（2）∵8×1.2=9.6<13.4
∴y=13.4应满足y=1.9x-5.6
∴13.4=1.9x-5.6 解得x=10
37、（南昌市2004）仔细观察下图，认真阅读对话：
根据对话的内容，试求出饼干和牛奶的标价各是多少元？
解：设饼干的标价为每盒x元，牛奶的标价为每袋y元，则
x+y>10,………………（1）
0.9x+y=10－0.8,…… （2）…………………………………………………………2分
x<10. ………（3）
由（2）得y=9.2－0.9x.……（4）
把（4）代入（1）得：9.2－0.9x+x>10,解得x>8.…………………………………4分
由（3）综合得 ∴8<x<10. ………………………………………………………5分
又∵x是整数，∴x=9.………………………………………………………………6分
把x=9代入（4）得：y=9.2－0.9×9=1.1（元）.…………………………………7分
答：一盒饼干标价9元，一袋牛奶标价1.1元.
38、（荆门2004）现用甲、乙两种运输车将46吨抗旱物资运往灾区，甲种运输车载重5吨，乙种运输车载重4吨，安排车辆不超过10辆，则甲种运输车至少应安排C
A．4辆 B．5辆 C．6辆 D．7辆
39、（荆门2004）为了改善城乡人民生产、生活环境，我市投入大量资金，治理竹皮河污染，在城郊建立了一个综合性污水处理厂，设库池中存有待处理的污水
吨，又从城区流入库池的污水按每小时
吨的固定流量增加.如果同时开动2台机组需30小时处理完污水，同时开动4台机组需10小时处理完污水.若要求5小时内将污水处理完毕，那么至少要同时开动多少台机组？
解：设1台机组每小时处理污水v吨，要在5小时内处理完污水，至少需开动x台机组，则……………………………………………………………………………………… 1分
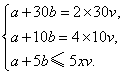（①②各1分，③2分，其中③写成等式不扣分）… 5分
由得
……………………………………………………………………… 7分
代入得
.
40、(淮安市2004) 国泰玩具厂工人的工作时间：每月25天，每天8小时．待遇：按件计酬，多劳多得，每月另加福利工资100元，按月结算．该厂生产A、B两种产品，工人每生产一件A种产品，可得报酬0．75元，每生产一件B种产品，可得报酬1．40元．下表记录了工人小李的工作情况：
| 生产A种产品件数(件) | 生产B种产品件数(件) | 总时间(分) |
| l | 1 | 35 |
| 3 | 2 | 85 |
根据上表提供的信息，请回答下列问题：
(1)小李每生产一件A种产品、每生产一件B种产品，分别需要多少分钟?
(2)如果生产各种产品的数目没有限制，那么小李每月的工资数目在什么范围之内?
解：(1)解：设小李每生产一件A种产品、每生产一件B种产品分别需要x分钟和y
分钟,根据题意,得
解之,得
（由记录表直接推出正确结论的，同样给分）
(2)方法一：设小李每月生产A种产品x件，B种产品y件(x、y均为非负整数)，月工资
数目为w元, 根据题意,得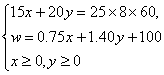
,即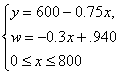
由于- 0．3<0，因此当x=O时，w最大=－O．3·0+940=940
当x=800时，w最小=－O.3·800+940=700．
因为生产各种产品的数目没有限制，所以700≤w≤940．
即小李每月的工资数目不低于700元而不高于940元．
方法二：由(1)知小李生产A种产品每分钟可获利O．05元，生产B种产品每分钟可获利O．07元， 若小李全部生产A种产品，每月的上资数目为700元，若小李全部生产B种产品，每月的工资数目为940元
小李每月的工资数目不低于700元而不高于940元．
41、(淮安市2004) 已知：两个正整数的和与积相等，求这两个正整数．
解：不妨设这两个正整数为a、b，且a≤b．
由题意，得ab=a+b，…………………………(*)
则ab=a+b≤b+b=2b，所以a≤2．
因为a为正整数，所以a=1或2．
①当a=1时，代入等式(*)，得1·b=1+b，b不存在；
②当a=2时，代入等式(*)，得2·b=2+b，b=2．
所以这两个正整数为2和2．
仔细阅读以上材料，根据阅读材料的启示，思考是否存在三个正整数，它们的和与积相等?试说明你的理由．
解：假设存在三个正整数，它们的和与积相等．
不妨设这三个正整数为a、b、c，且a≤b≤c，则abc=a+b+c (※)
所以abc=a+b+c≤c+c+c=3c，所以ab≤3，
若a≥2，则b≥a≥2，所以ab≥4，与ab≤3矛盾。
因此a=l，b=l或2或3，
① 当a=l，b=l时，代入等式(※)得l+l+c=1·1·c，c不存在；
⑦ 当a=l，b=2时，代入等式(※)得1+2+c=1·2·c，c=3；
③ 当a=1，b=3时，代入等式(※)得1+3+c=1·3·c，c=2；与b≤c矛盾，舍去
所以a=1，b=2，c=3，因此假设成立．即存在三个正整数，它们的和与积相等．
42、（日照市2004）已知关于的不等式组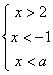
，无解，则的取值范围是
（ D ）
A 
B 
C 
D 
43、（2004年河北）光华农机租赁公司共有50台联合收割机，其中甲型20台，乙型30台.现将这50台联合收割机派往A、B两地区收割小麦，其中30台派往A地区，20台派往B地区.
两地区与该农机租赁公司商定的每天的租赁价格见下表：
| 每台甲型收割机的租金 | 每台乙型收割机的租金 | |
| A地区 | 1800元 | 1600元 |
| B地区 | 1600元 | 1200元 |
（1）设派往A地区x台乙型联合收割机，租赁公司这50台联合收割机一天获得的租金为y(元)，求y与x间的函数关系式，并写出x的取值范围；
（2）若使农机租赁公司这50台联合收割机一天获得的租金总额不低于79600元，说
明有多少种分派方案，并将各种方案设计出来；
（3）如果要使这50台联合收割机每天获得的租金最高，请你为光华农机租赁公司提
出一条合理建议.
解：（1）若派往A地区的乙型收割机为x台，则派往A地区的甲型收割机为(30-x)台；派往B地区的乙型收割机为（30-x）台，派往B地区的甲型收割机为（x-10）台.
∴y=1600x+1800(30-x)+1200(30-x)+1600(x-10)=200x+74000.
x的取值范围是：10≤x≤30(x是正整数).
（2）由题意得200x+74000≥79600,
解不等式得x≥28.由于10≤x≤30，∴x取28，29，30这三个值，
∴有3种不同分配方案.
① 当x=28时，即派往A地区甲型收割机2台，乙型收割机28台；派往B
地区甲型收割机18台，乙型收割机2台.
② 当x=29时，即派往A地区甲型收割机1台，乙型收割机29台；派往B
地区甲型收割机19台，乙型收割机1台.
③ 当x=30时，即30台乙型收割机全部派往A地区；20台甲型收割机全部派往B地区.
（3）由于一次函数y=200x+74000的值y是随着x的增大而增大的，所以，当x=30时，y取得最大值.如果要使农机租赁公司这50台联合收割机每天获得租金最高，只需x=30，此时，y=6000+74000=80000.
建议农机租赁公司将30台乙型收割机全部派往A地区；20台甲型收割要全部派往B地区，可使公司获得的租金最高.
44、（湖州市2004）织里某童装加工企业今年五月份工人每人平均加工童装150套，最不熟练的工人加工的童装套数为平均套数的60%。为了提高工人的劳动积极性，按时完成外商订货任务，企业计划从六月份起进行工资改革。改革后每位工人的工资分二部分：一部分为每人每月基本工资200元；另一部分为每加工1套童装奖励若干元。
（1）为了保证所有工人的每月工资收入不低于市有关部门规定的最低工资标准450元，按五月份工人加工的童装套数计算，工人每加工1套童装企业至少应奖励多少元（精确到分）？
（2）根据经营情况，企业决定每加工1套童装奖励5元。工人小张争取六月份工资不少于1200元，问小张在六月份应至少加工多少套童装？
解：（1）设企业每套奖励x元， 由题意得：200+60%·150x≥450
解得：x≥2.78 因此，该企业每套至少应奖励2.78元。
（2）设小张在六月份加工y套 由题意得：200+5y≥1200 解得：y≥200。
45、（2004年福建三明）已知不等式组
有解,则的取值范围为
（A）＞-2 （B）≥-2 （C）＜2 （D）≥2 .
答：［
C ］