【巩固练习】(答题时间:100分钟)
一、选择题(每题3分,共18分)
1. 下列四个函数中,当x>0时,随x增大而增大的函数是( )
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
2. 纳米是一种长度单位,一纳米=![]() 。已知某种植物花粉的直径约为35000纳米,那么用科学记数法表示这种花粉的直径为( )
。已知某种植物花粉的直径约为35000纳米,那么用科学记数法表示这种花粉的直径为( )
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
3. 过O内一点M的最长弦为6cm,最短的弦为4cm,则OM的长为( )
A. 3cm B. 2cm
C. ![]() cm D.
cm D.
![]() cm
cm
4. 某校九年级毕业时,每一个同学都将自己的像片向全班其他同学各送一张表示留念。全班共送了2250张像片,如果全班有x名学生,根据题意列出方程为( )
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
5. 如图所示,把一个正方形三次对折后沿虚线剪下,则所得的图形是( )
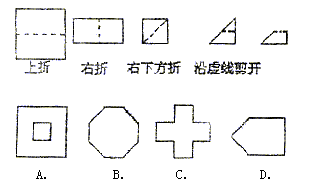
6. 若一次函数![]() 的图象经过二、三、四象限,则二次函数
的图象经过二、三、四象限,则二次函数![]() 的图象只可能是( )
的图象只可能是( )
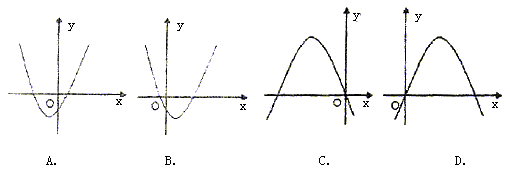
二、填空题(每题3分,共18分)
7. 计算:![]() ___________。
___________。
8. 已知两圆半径分别为3cm和7cm,如果两圆相切,则圆心距d=___________;
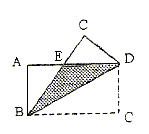
9. 如图,矩形ABCD中,AB=3,BC=4,如果将该矩形沿对角线BD折叠,那么图中阴影部分的面积是___________。
10. 小明把如图所示的4张扑克牌放在一张桌子上,请一位同学避开他任意将其中一张牌旋转倒过来,然后小明很快辨认了哪张牌被倒过来了,那么图中被倒过来的扑克牌是___________,其辨认所依据的数学知识是___________。

11. 某种商品的进价为800元,出售时的标价为1200元,后来由于该商品积压,商店准备打折出售,但要保持利润率不低于5%,则至少可打___________折。
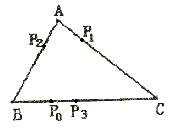
12. 电子跳蚤游戏盘(如下图)为△ABC,AB=8,AC=9,BC=10,如果电子跳蚤开始时在BC边的P0点,BP0=4,AC边上P1点,且CP1=CP0;第二步跳蚤从P1跳到AB边上,三步跳蚤从P2跳回到BC边上P3点,且BP3=BP2;……跳蚤按上述规则跳下去,第2003次落点为P2003,则P3与P2003之间的距离为___________。
三、作图题(本题满分6分)
13. 如图,有一座石拱桥的桥拱是一段圆弧AB。

(1)请你确定弧AB所在圆的圆心O;
(2)连接OA、OB,若⊙O的直径为8,∠AOB=120°,请求出石拱桥的长度。
四、解答题(本题满分78分,共有9道小题)
14. (本小题满分6分)
解方程组:![]()
15. (本小题满分6分)
下面两幅统计图(如图1、图2),反映了某市甲、乙两所中学学生参加课外活动的情况。请你通过图中信息回答下面的问题。
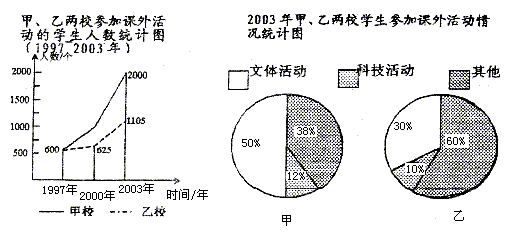
图1 图2
(1)通过对图1的分析,写出一条你认为正确的结论;(3分)
(2)通过对图2的分析,写出一条你认为正确的结论;(3分)
(3)2003年甲、乙两所中学参加科技活动的学生人数共有多少?(4分)
16. (本小题满分6分)
依据闯关游戏规则,请你探究“闯关游戏”的奥秘;闯关游戏规则:如图所示的面板上,有左右两组开关按钮,每组中的两个按钮均分别控制一个灯泡和一个发音装置。同时按下两组中各一个按钮;当两个灯泡都亮时闯关成功;当按错一个或两个按钮时,发音装置就会发出“闯关失败”的声音。
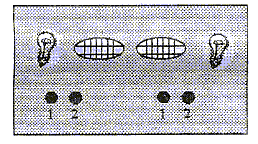
(1)用列表的方法表示有可能的闯关情况;
(2)求出闯关成功的概率。
17. (本小题满分8分)
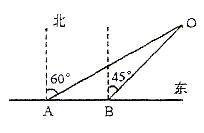
如图所示,某船由西向东航行,在点A测得小岛O在北偏东60°,船行了10海里后到达点B,这时测得小岛O在北偏东45°。由于以小岛O为圆心16海里为半径的范围内有暗礁,如果该船不改变航向继续航行,有没有触礁的危险?通过计算说明。(供选用数据:![]() )
)
18. (本小题满分8分)
小东到超市购物,认真阅读小东和售货员的对话,小东:“阿姨,我买一盒饼干和一袋牛奶。”(递上10元钱)
售货员:“小朋友,本来你用10元钱买一盒饼干是有余的,但要再买一袋牛奶就不够了!今天是儿童节,我给你买的饼干打九折,两样东西请拿好!还有找你的8角钱。”饼干的价钱是整数。
你能帮小东求出饼干和牛奶的标价各是多少元吗?
19. (本小题满分8分)
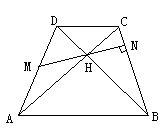
梯形ABCD中AB∥CD,对角线AC、BD垂直相交于H,M是AD上的点,MH所在直线交BC于N。在以上前提下,试将下列设定中的两个作为题设,另一个作为结论组成一个正确的命题,并证明这个命题。①AD=BC,②MN⊥BC,③AM=DM。
20. (本小题满分8分)
某工厂设门市部专卖某产品,该产品每件成本40元,从开业一段时间的每天销售统计中,随机抽取一部分情况如下表所示:
| 每件销售价(元) | 50 | 60 | 70 | 75 | 80 | 85 | … |
| 每天售出件数 | 300 | 240 | 180 | 150 | 120 | 90 | … |
假设当天定的售价是不变的,且每天销售情况均服从这种规律。
(1)观察这些统计数据,找出每天售出件数y与每件售价x(元)之间的函数关系,并写出该函数关系式。
(2)门市部原设有两名营业员,但当销售量较大时,在每天售出量超过168件时,则必须增派一名营业员才能保证营业有序进行,设营业员每人每天工资为40元。
求每件产品应定价多少元,才能使每天门市部纯利润最大(纯利润指的是收入总价款扣除成本及营业员工资后的余额,其它开支不计)
21. (本小题满分12分)
等腰Rt△ABC的直角边AB=2,点P、Q分别从A、C两点同时出发,以相同速度做直线运动,已知点P沿直线AB运动,点Q沿边BC的延长线运动,PQ与直线AC相交于点D。
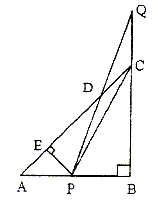
(1)设AP的长为x,△PCQ的面积为S,求出S关于X的函数关系式
(2)当AP的长为何值时,![]()
(3)当P在线段AB上时,作PE⊥AC于点E,当点P、Q运动时,线段DE的长度是否改变?证明你的结论。
22. (本小题满分12分)
请阅读下面的材料,并回答所提出的问题。
三角形内角平分线性质定理:三角形的内角平分线分对边所得的两条线段和这个角的两边对应成比例。
已知:如图,△ABC中,AD是角平分线,求证:![]()
分析:要证![]() ,一般只要证BD、DC与AB、AC或BD、AB与DC、AC所在的三角形相似。现在B、D、C在一直线上,△ABD与△ADC不相似,需要考虑用别的方法换比。
,一般只要证BD、DC与AB、AC或BD、AB与DC、AC所在的三角形相似。现在B、D、C在一直线上,△ABD与△ADC不相似,需要考虑用别的方法换比。
在比例式![]() 中,AC恰是BD、DC、AB的第四比例项,所以考虑过C作CE∥AD,交BA的延长线于E,从而得到BD、DC、AB的第四比例项AE,这样,证明
中,AC恰是BD、DC、AB的第四比例项,所以考虑过C作CE∥AD,交BA的延长线于E,从而得到BD、DC、AB的第四比例项AE,这样,证明![]() 就可以转化为证AE=AC。
就可以转化为证AE=AC。
证明:过C作CE∥DA,交BA的延长线于E。(完成以下证明过程)

问题:
①上述证明过程中,用到了哪些定理?(写对两个定理即可)。
②在上述分析、证明过程中,主要用到了下列三种数学思想中的哪一种?选出一个填在后面的括号内( )
A. 数形结合的思想;
B. 转化思想;
C. 分类讨论思想;
③用三角形内角平分线性质定理解答问题:
已知:如图,△ABC中,AD是角平分线,AB=5cm,AC=4cm,BC=7cm。
求:BD的长。
![]()
【试题答案】
一、选择题:
1. C 2. B 3. C
4. A 5. C 6. C
二、填空题:
7. 0 8. 4cm或10cm
9. ![]() 10.
5 中心对称图形
10.
5 中心对称图形
11. 7 12. 4.5
三、作图题
13. (1)
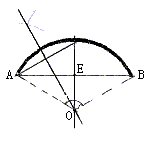
点O为弧AB所在圆的圆心。
(2)![]()
=![]()
14. 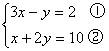
解①得
![]() ③
③
③代入②
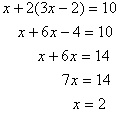
把x=2代入①
6-y=2
-y=-4
y=4
∴此方程组的解为![]()
15. (1)甲比乙的增长快;
(2)甲校参加文体活动的人数最多;
(3)351人
16.
(1)
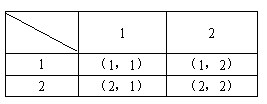
(2)闯关成功的概率为![]() 。
。
17.
解: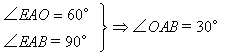
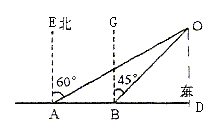
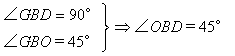
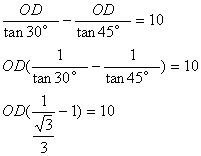
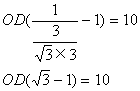
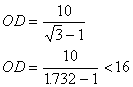
∴有触礁的危险
18. 解:设:饼干的标价为x元,牛奶的标价为![]()
![]()
![]()
∴x=9
∴![]() 元
元
答:饼干9元;牛奶1.1元。
19. 已知:AD=BC,AM=DM
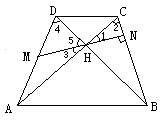
求证:MN⊥BC
证明:∵AB∥CD
AD=BC
∴∠DAB=∠CBA,∵AB=BA
∴△ABC≌△ADB
∴∠4=∠2
又∵MH是直角△ADH的中线
∴MH=MD
∴∠4=∠5
又∵∠3+∠5=90°,∠3=∠1
∴∠1+∠2=90°
∴MN⊥BC
20. (1)![]()
(2)当x=70时最大利润5320元。
21. (1)![]()
(2)当![]() 时
时
(3)DE长度不会改变,证明略
22. ①两线平行同位角相等,等角对等边
②B
③![]()