| | 初中数学中学了一次方程(组)、一元二次方程以及简单的分式方程、根式方程、二元二次方程。中考中的方程知识综合题,多以一元二次方程为热点,且以判别式、韦达定理的灵活运用为主要考点。这类题,以考查灵活的代数(整式、分式、根式)变换和转化能力为基础的。此外,在2000年的中考卷中,还有一些设计独特的方程知识探索题颇具新意。
一、典型试题选析(本文所有选题均为2000年中考题)
例1:(湖北省鄂州市)
已知关于x的方程kx2+(2k-1)x-2=0。
(1)若方程有实根,求k的取值范围。
(2)若此方程两实根为x1、x2且x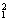 +x +x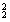 =3,求k的值。 =3,求k的值。
解:(1)依题意得:Δ≥0,∴(2k-1)2-4k(k-2)≥0,解得k≥-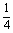 , ,
∴k的取值范围是k≥-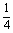 。 。
(2)依题意得:x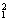 +x +x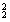 =(x1+x2)2-2x1x2=3,即:(- =(x1+x2)2-2x1x2=3,即:(-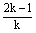 )2-2· )2-2·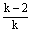 =3, =3,
化简得k2=1,∴k=±1。
上面解答有无错误?若有指出错误之处,并直接写出正确答案。
解:上面两题均有错误。正确解答是:
(1)分k=0,k≠0两种情况:
当k=0,方程为一元一次方程-x-2=0,方程有实数解x=-2;
当k≠0,方程为一元二次方程,依题意得Δ≥0,∵(2k-1)2-4k(k-2)≥0,解得k≥-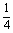 ≥0,此时k的取值范围是k≥- ≥0,此时k的取值范围是k≥-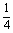 且k≠0。 且k≠0。
综合上述两种情况,k的取值范围是k≥-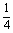 。 。
(2)解题过程略。解得k=±1之后,同时考虑有实根的条件k≥-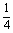 ,应排除k=-1,∴k=1。 ,应排除k=-1,∴k=1。
说明:本题已知方程未说明是一元二次方程,因此首先要分k=0,k≠0两种情况讨论,这点,容易忽视;其次,韦达定理应用的前提是有实根,即Δ≥0,这点,也容易被疏漏,本题既考查方程、韦达定理、判别式的基本概念,也考查学生周密思考能力。
例2:(山东淄博市)
(1)如表,方程1,方程2,方程3,……,是按照一定规律排列的一列方程。解方程1,并将它的解填在表中的空白处;
(2)若方程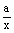 - -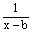 =1(a>b)的解是x1=6,x2=10,求a、b的值。该方程是不是(1)中所给出的一列方程中的一个方程?如果是,它是第几个方程? =1(a>b)的解是x1=6,x2=10,求a、b的值。该方程是不是(1)中所给出的一列方程中的一个方程?如果是,它是第几个方程?
(3)请写出这列方程中的第n个方程和它的解,并验证所写出的解适合第n个的方程。 | 序号 | 方程 | 方程的解 | | 1 | 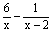 =1 =1
| x1=______ | x2=______ | | 2 | 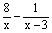 =1 =1
| x1=4 | x2=6 | | 3 | 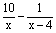 =1 =1
| x1=5 | x2=8 | | … | … | … | … | 解:(1)x1=3,x2=4;
(2)将x1=6,x2=10代入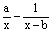 =1,可得方程组 =1,可得方程组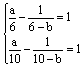 , ,
化简可得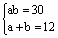 。 。
∵a>b,又可得a=6+2 ,b=6-2 ,b=6-2 ,∴原方程应是 ,∴原方程应是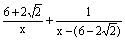 =1。这显然不是表列的系列方程中的一个,因为表中规律可推知第4个方程是: =1。这显然不是表列的系列方程中的一个,因为表中规律可推知第4个方程是: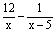 =1,其解也是x1=6,x2=10。 =1,其解也是x1=6,x2=10。
(3)由表中规律可以猜测第n个方程是:
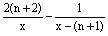 =1(n是自然数)(*) =1(n是自然数)(*)
方程的解为:x1=n+2,x2=2(n+1)。
验证:解方程(*),去分母并整理可得:
x2-[(n+2)+2(n+1)]x+2(n+1)(n+2)=0,∴x1=n+2,x2=2(n+1)。
说明:本题综合了方程的许多知识:解分式方程;列分式方程组并解答;解一元二次方程等。除此之外,本题提出了较高的综合素质的要求:要会观察,找出系列方程中的规律;个例验证,正确验证第(2)题;探索一般规律,完成第(3)题。本题设计突破了传统模式。
例3:(江苏南通市)
设x1、x2是关于x的方程x2-(k+2)x+2k+1=0的两个实数根,且x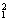 +x +x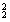 =11。 =11。
(1)求k的值;
(2)利用根与系数的关系求一个一元二次方程,使它的一个根是原方程两个根的和,另一根是原方程两根差的平方。
解:(1)由韦达定理知:x1+x2=k+2,x1x2=2k+1。
∵x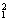 +x +x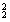 =(x1+x2)2-2x1x2=(k+2)2-2(2k+1)=k2+2=11,∴k=±3。 =(x1+x2)2-2x1x2=(k+2)2-2(2k+1)=k2+2=11,∴k=±3。
k=3时,原方程为x2-5x+7=0,此时Δ<0,无实根,不合题意,舍去。故k=-3。
(2)∵k=-3,故方程为x2+x-5=0,设此方程两根为x1、x2,则可得x1+x2=-1,x1x2=-5。
而(x1-x2)2=(x1+x2)2-4x1x2=(-1)2-4×(-5)=21。
∵所求新方程的两根分别为x1+x2=-1和(x1-x2)2=21,故新方程是x2-(-1+21)x+(-1)·21=0,即x2-20x-21=0。
说明:已知一元二次方程根的对称式求待定系数时,不仅要逆用韦达定理,更要注意判别式的检验;求作新的一元二次方程x2+px+q=0时,关键在于确定两个数值p=-(x1+x2),q=x1x2,其x1,x2是新方程的两根。
例4:(山东聊城市)
已知关于x的方程x2+2x+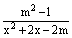 =0,其中m为实数。 =0,其中m为实数。
(1)当m为何值时,方程没有实数根?
(2)当m为何值时,方程恰有三个互不相等的实数根?求出这三个实数根。
解:(1)令x2+2x-2m=y,则原方程化为y2+2my+m2-1=0,
解得:y1=-m+1,y2=-m-1(显然m=±1时,原方程有实数根)。
由此得x2+2x-m-1=0 ①
或x2+2x-m+1=0 ②
对于①由Δ1=22-4(-m-1)<0得,m<-2;
对于②由Δ2=22-4(-m+1)<0得,m<0,
∴当m<-2,原方程没有实数根。
(2)由(1)可得:
当m=-2时,方程①有两个相等的实数根,但此时,方程②没有实数根,不合题意;
当m=0时,方程②有两个相等的实数根x=-1,此时方程①有两个不相等的实数根x=-1± ,∴当m=0时,原方程有三个互不相等的实数根x1=-1,x2=-1+ ,∴当m=0时,原方程有三个互不相等的实数根x1=-1,x2=-1+ ,x3=-1- ,x3=-1- 。 。
说明:本题综合了分式方程、一元二次方程根的判别式等知识点,换元法是本题的主要数学思想方法。
例5:(大连市)阅读下列材料:
∵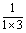 = =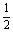 (1- (1-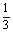 ), ),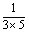 = =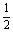 ( (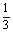 - -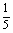 ), ),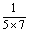 = =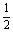 ( (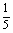 - -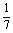 ),…, ),…,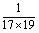 = =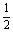 ( (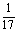 - -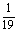 ), ),
∴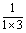 + +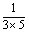 + +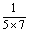 +…+ +…+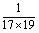 = =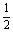 (1- (1-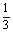 )+ )+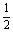 ( (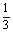 - -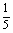 )+ )+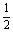 ( (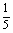 - -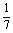 )+…+ )+…+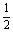 ( (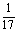 - -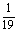 )= )=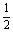 (1- (1-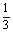 + +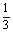 - -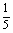 + +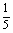 - -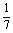 +…+ +…+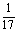 - -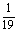 )= )=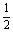 (1- (1-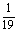 )= )= 。 。
解答问题:
(1)在上式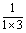 + +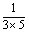 +…中,第五项中____,第n项为_____,上述求和的想法是:通过逆用____法则,将上式中各分数转化为两个实数之差,使得除首末两项外的中间各项可以_____,从而达到求和目的。 +…中,第五项中____,第n项为_____,上述求和的想法是:通过逆用____法则,将上式中各分数转化为两个实数之差,使得除首末两项外的中间各项可以_____,从而达到求和目的。
(2)解方程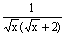 + +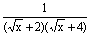 +…+ +…+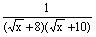 = =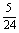 。 。
解:(1)分别填入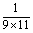 , ,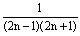 ,分数减法,互相抵消。 ,分数减法,互相抵消。
(2)原方程可化为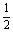 ( (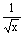 - -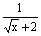 + +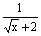 - -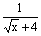 +…+ +…+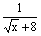 - -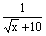 )= )=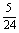 ,即 ,即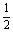 ( (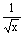 - -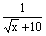 )= )=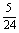 。 。
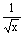 - -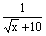 = =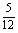 , ,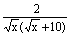 = =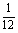 , ,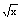 ( (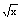 +10)=24,( +10)=24,(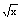 +12)( +12)(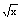 -2)=0, -2)=0,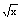 =-12(舍去),由 =-12(舍去),由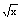 =2得,x=4。 =2得,x=4。
经检验,x=4是原方程的根。
说明:本题从求数列之和到解一个特殊的根式方程,介绍的是一类分式裂项求和的数学方法及其应用。
二、小结
方程知识综合题涉及有关方程的基础概念、解法,判别式及韦达定理是一元二次方程中应用较广、充满活力的知识点;判别式及韦达定理的灵活运用解题又涉及整式、分式、根式及不等式的许多的知识、技能;以上例题中,一些创意较新的试题还涉及到其他多方面的知识,应该引起大家的注意。
三、练习题(均选自2000年中考卷)
1、(北京朝阳区)
(1)解下列方程:
x2-2x-2=0 ①; 2x2+3x-1=0 ②; 2x2-4x+1=0 ③; x2+6x+3=0 ④。
(2)上面的四个方程中,有三个方程的一次项系数有共同特点,请你用代数式表示这特点,并推导出具有这个特点的一元二次方程的求根公式。
2、(青岛市)
先阅读下列解方程(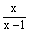 )2- )2-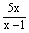 +6=0的过程,然后填空: +6=0的过程,然后填空:
解:(第一步)设y=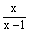 ,则原方程可化为y2-5y+6=0。 ,则原方程可化为y2-5y+6=0。
(第二步)解这个方程得:y1=2,y2=3。
(第三步)当y1=2时,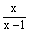 =2,则x1=2; =2,则x1=2;
当y2=3时,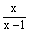 =3,则x2= =3,则x2=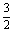 。 。
(第四步)∴原方程的根为x1=2,x2=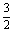 。 。
以上解题过程中的第一步用的是_____法:上述解题过程不完整,缺少的一步是_____。
3、(湖北潜江市)
使关于x的分式方程a2-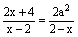 产生增根的a的值是: 产生增根的a的值是:
(A)2 (B)-2 (C)±2 (D)与a无关
4、(安徽省)
一个二元一次方程和一个二元二次方程组成的二元二次方程组的解是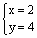 和 和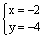 ,试写出符合要求的方程组______。(只要填写一个即可)。 ,试写出符合要求的方程组______。(只要填写一个即可)。
5、(兰州市)
已知三角形两边长分别为2和9,第三边的长是二次方程x2-14x+48=0的根,则这个三角形的周长为( )
(A)11 (B)17 (C)17或19 (D)19
6、(湖北省天门市)
关于x的方程kx2-6x+3=0有实数根,则k的非负整数值是( )
(A)0,1,2 (B)1,2 (C)1.2,3 (D)0,1,2,3
7、(湖北省天门市)
已知关于x的方程x2+(a2+2a-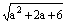 )x+a=0有两实数根,且互为相反数,求a的值。 )x+a=0有两实数根,且互为相反数,求a的值。
8、(湖北黄冈市)
先阅读下列第(1)题的解答过程,然后再解答第(2)题。
(1)已知实数a,b满足a2=2-2a,b2=2-2b,且a≠b,求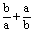 的值。 的值。
解法1:由已知得a2+2a-2=0,b2+2b-2=0,且a≠b。
∴a,b是方程x2+2x-2的两个不相等的实数根。
由根与系数的关系,得a+b=-2,ab=-2。
∴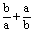 = =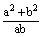 = =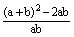 = =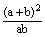 -2= -2=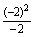 -2=-4。 -2=-4。
解法2:由已知a2=2-2a ①
b2=2-2b ②
①-②,得(a2-b2)+2(a-b)=0,即(a-b)(a+b+2)=0。
∵a≠b,∴a+b+2=0,∴a+b=-2。
①×②,得a2b2=(2-2a)(2-2b),即(ab)2-4ab-12=0,∴ab=6或ab=-2。
显然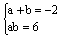 无实数解,∴a+b=-2,ab=-2。 无实数解,∴a+b=-2,ab=-2。
∴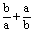 = =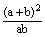 -2= -2=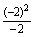 -2=-4。 -2=-4。
(2)已知p2-2p-5=0.5q2+2q-1=0,其中p、q为实数,求p2+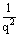 的值。 的值。
9、(湖北孝感市)
已知m、n是一元二次方程x2+5x-3=0的两根,求代数式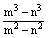 的值。 的值。
10、(湖北鄂州市)
x1、x2为两实数,且满足条件2x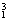 +4x1-3=0,2x +4x1-3=0,2x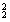 +4x2-3=0,则 +4x2-3=0,则 + +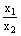 的值为( ) 的值为( )
(A)2或-4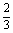 (B)2或 (B)2或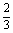 (C) (C)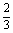 (D)-4 (D)-4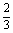
11、(湖北黄石市)
已知a、b满足a2-2a-1=0,b2-2b-1=0,则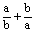 =_______。 =_______。
12、(湖北潜江市)
若一元二次方程x2-ax-4a=0的两实根之和为4a2-3,则两根之积为( )
(A)-4 (B)3或-4 (C)3 (D)-3或4
13、(浙江绍兴市)
若方程(x-1)(x2+8x-3)=0的三根分别为x1、x2、x3,则x1x2+x2x3+x3x1的值是( )
(A)5 (B)-5 (C)11 (D)-11
14、(湖北天门市)
若方程x2-2x-3=0的两根是x1、x2,则代数式x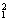 +x +x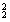 -2x1-2x2的值是_______。 -2x1-2x2的值是_______。
15、(辽宁省)
已知α、β是方程x2+2x-5=0的两个实数根,则α2+αβ+2α的值为______。
16、(广东省)
设x1、x2是方程x2-5x+3=0的两个根,不解这个方程,利用根与系数的关系,求(x1-x2)2的值。
17、(宁波市)
已知方程x2+2x-3k=0的两个根分别是x1和x2,且满足(x1+1)(x2+1)=-4,求k的值。
18、(苏州市)
已知关于x的方程x2+(m-2)x+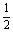 m-3=0。 m-3=0。
(1)求证:无论m取什么实数值,这个方程总有两个不相等的实数根;
(2)若这个方程的两个实数根x1、x2满足2x1+x2=m+1,求m的值。
19、(北京市海淀区)
已知:关于x的方程x2+3x+a=0 ①的两个实数根的倒数和等于3,关于x的方程(k-1)x2+3x-2a=0 ②有实数且k为正整数,求代数式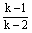 的值。 的值。
20、(山东济南市)
已知关于x的方程x2-2(m-2)x+m2=0。
问:是否存在实数m,使方程的两个实数根的平方和等于56,若存在,求出m的值;若不存在,请说明理由。
21、(上海市)
已知关于x的一元二次方程mx2-(2m-1)x+m-2=0(m>0)
(1)求证:这个方程有两个不相等的实数根;
(2)如果这个方程的两个实数根分别为x1、x2,且(x1-3)(x2-3)=5m,求m的值。
22、(江苏泰州市)
已知关于x的一元二次方程x2+2px-p2-1=0的两个实数根为x1和x2。
(1)若此方程的两根之和不大于两根之积,求p的值;
(2)若p=-1,求x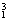 +2x +2x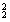 +2x2的值。 +2x2的值。
23、(江苏宿迁市)
设a,b的方程x2+5x+2=0的两根,则以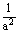 、 、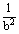 为根的一元二次方程是( ) 为根的一元二次方程是( )
(A)21x2-4x+1=0 (B)4x2-21x+1=0
(C)21x2-4x-1=0 (D)4x2-21x-1=0
24、(贵州省黔东南州)
一次函数y=-2x+3图象与坐标轴交点分别为(a,0)和(0,b),则以a、b为两根的一元二次方程是______。
25、(广州市压轴题)
已知:关于x的方程x2+4x+2t=0有两个实数根。
(1)求t的取值范围;
(2)设方程的两个实数根的倒数的和为S,求S关于t的函数的解析式;
(3)画出(2)中所得到的函数的图象。
答案:
1、(1)略;(2)方程①、③、④一次项系数为偶数2n(n为整数),x=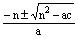 ; ;
2、换元,检验;
3、C;
4、(略);
5、D;
6、A;
7、-3;
8、14或14±4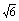 ; ;
9、-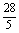 ; ;
10、A;
11、2或-6;
12、A 13、D
14、6;
15、0;
16、13;
17、1;
18、(1)Δ=(m-3)2+16>0;(2)0或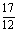 ; ;
19、0;
20、m=-2;
21、(1)Δ=4m+1>0(∵m>0);(2)m=1或-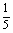 ; ;
22、(1)p=1;(2)20;
23、B;
24、2x2-9x+9=0;
25、(1)t≤2;(2)S=-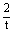 (t≤2);(3)图略。 (t≤2);(3)图略。 载自《理科考试研究》 | |