绝密★启用前 试卷类型：A
威海市二○○五年初中升学考试
数 学
（时间120分钟，满分120分）
请同学们注意：
1．答卷前请将密封线内的项目填写清楚．
2．本试卷分第 I 卷和第 II 卷两部分，共10页．第 I 卷（1至2页）为选择题，第 II 卷（3至10页）为非选择题．第 I 卷（选择题）的答案须填写在第3页的答案表中，第 II 卷（非选择题）直接答在试卷上．考试结束时，将试卷全部上交．
3．凡要求保留精确度的题目，要用计算器计算，计算过程中的数据不要四舍五入；不要求保留精确度的题目，计算结果保留准确值．
第 I 卷 （选择题，共36分）
一、选择题（本大题共12小题, 每小题3分, 共36分. 在每小题给出的四个选项中，只有一个是正确的. 每小题选对得3分，选错、不选或多选，均不得分）
1．下列计算结果正确的是
（A）
（B）
=
（C）
（D）
2．不等式组
的解集为
（A）2＜x＜3 （B）x＞3 （C）x＜2 （D）x＞2或 x＜-3
3．在△ABC和△DEF中，已知∠C＝∠D，∠B＝∠E，要判定这两个三角形全等，还需要条件
（A）AB＝ED （B）AB＝FD （C）AC＝FD （D）∠A＝∠F
4．计算
的结果是
（A）
（B）
（C）
（D）
5．关于x的一元二次方程
的根的情况是
（A）有两个相等的实数根 （B）有两个不相等的实数根
（C）没有实数根 （D）无法判断
6．化简
的结果是
（A）
（B）
（C）
（D）
7．若圆锥侧面积是底面积的2倍，则这个圆锥的侧面展开图的圆心角是
（A）120˚ （B）135˚ （C）150˚ （D）180˚
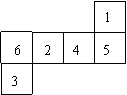8．下图可以沿线折叠成一个带数字的立方体，每三个带数字的面交于立方体的一个顶点，则相交于一个顶点的三个面上的数字之和最小是
（A） 7
（B） 8
（C） 9
（D） 10
9．用两种正多边形镶嵌，不能与正三角形匹配的正多边形是
（A）正方形 （B）正六边形 （C）正十二边形 （D）正十八边形
10．如图，数轴上表示1，
的对应点分别为点A，点B．若点B关于点A的对称点为点C，则点C所表示的数是
（A）
（B）
（C）
（D）
11．如图，E，G，F，H分别是矩形ABCD四条边上的点，EF⊥GH，若AB＝2，
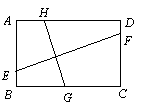BC＝3，则EF︰GH＝
（A） 2︰3
（B） 3︰2
（C） 4︰9
（D） 无法确定
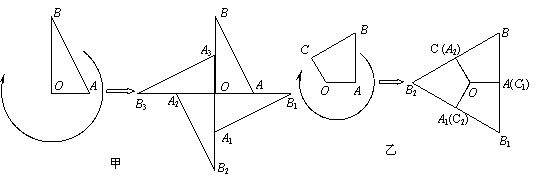12．如图所示，在图甲中，Rt△OAB绕其直角顶点O每次旋转90˚，旋转三次得到右边的图形．在图乙中，四边形OABC绕O点每次旋转120˚，旋转二次得到右边的图形．
下列图形中，不能通过上述方式得到的是
绝密★启用前 试卷类型：A
威海市二○○五年初中升学考试
数 学
第 II 卷 （非选择题，共84分）
注意事项：
1. 第 I 卷（选择题）的答案填写在下面的答案表中．
2. 第Ⅱ卷共8页，用兰、黑色钢笔或圆珠笔直接答在试卷上．
选择题答案表
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 得 分 | 评卷人 |
| 答案 |
二、填空题（本大题共6小题，每小题3分，共18分. 只要求填出最后结果）
13．“五一”黄金周期间，梁先生驾驶汽车从甲地经过乙地到丙地游玩．甲地到乙地有2条公路，乙地到丙地有3条公路．每一条公路的长度如下图所示(单位：km)．梁先生任选一条从甲地到丙地的路线，这条路线正好是最短路线的概率是 ．
 |
14．如图：梯形纸片ABCD，∠B＝60°，AD∥BC，AB＝AD＝2，BC＝6．将纸片折叠，使点B与点D重合，折痕为AE，则CE＝ ．
15．已知双曲线
经过点（－1，3），如果A(
)，B(
)两点在该双曲线上，且
＜
＜0，那么
．
16．若
，ab＝4，则
＝
．
17．一组按规律排列的数：
，
，
，
，
，…．
请你推断第9个数是 ．
18．在矩形ABCD中，AB＝5，BC＝12，若分别以点A，C为圆心的两圆相切，点D在⊙C内，点B在⊙C外，则⊙A的半径r的取值范围是 ．
三、解答题（本大题共7小题，共66分）
19.（本小题满分7分）
解方程：
．
20.（本小题满分7分）
为了解中学生的体能情况，某校随机抽取了部分学生进行一分钟跳绳次数测试．某同学将所得的数据进行整理，列出下表（未完成）：
| 分组（跳绳次数x） | 频数（学生人数） | 频 率 |
| 60≤x<80 | 2 | |
| 80≤x<100 | 0.1 | |
| 100≤x<120 | 17 | 0.34 |
| 120≤x<140 | 0.3 | |
| 140≤x<160 | 8 | 0.16 |
| 160≤x<180 | 3 | n |
| 合计 | m |
（1）求出上表中m，n的值；
（2）一分钟跳绳次数小于100的学生人数占被测试学生总数的百分之几？
（3）这次测试中，学生跳绳次数的中位数落在哪个范围内？并说明理由．
21.（本小题满分8分）
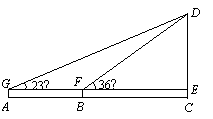某校数学兴趣小组的同学用学到的解直角三角形知识测量操场上旗杆的高度．如图，在操场上的A处，他们利用测角仪器测得旗杆CD顶端的仰角为23˚，再沿AC方向前进20米到达B处，又测得旗杆CD顶端的仰角为36˚，已知测角仪器的高度为1.2米，求旗杆CD的高度（精确到0.1米）．
22.（本小题满分10分）
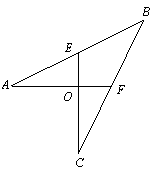如图，AF⊥CE，垂足为点O，AO＝CO＝2，EO＝FO＝1．
（1）求证：点Ｆ为BC的中点；
（2）求四边形BEOF的面积．
23.（本小题满分10分）
甲、乙两家体育器材商店出售同样的乒乓球拍和乒乓球，球拍一付定价60元，乒乓球每盒定价10元．今年世界乒乓球锦标赛期间，两家商店都搞促销活动：甲商店规定每买一付乒乓球拍赠二盒乒乓球；乙商店规定所有商品9折优惠．某校乒乓球队需要买2付乒乓球拍，乒乓球若干盒（不少于4盒）．
设该校要买乒乓球x盒，所需商品在甲商店购买需用y1元，在乙商店购买需用y2元．
（1）请分别写出y1，y2与x之间的函数关系式（不必注明自变量x的取值范围）；
（2）对x的取值情况进行分析，试说明在哪一家商店购买所需商品比较便宜．
（3）若该校要买2付乒乓球拍和20盒乒乓球，在不考虑其他因素的情况下，请你设计一个最省钱的购买方案．
24.（本小题满分12分）
已知抛物线
过点A (4，0)．
（1）试确定抛物线的解析式及顶点B的坐标；
（2）在y轴上确定一点P，使线段AP + BP最短，求出P点的坐标；
（3）设M为线段AP的中点，试判断点B与以AP为直径的⊙M的位置关系，并说明理由．
25.（本小题满分12分）
已知：如图1，在⊙O中，弦AB＝2，CD＝1，AD⊥BD．直线AD，BC相交于点E．
（１） 
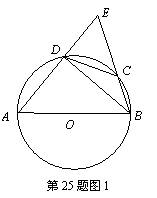求∠E的度数；
（2）如果点C，D在⊙O上运动，且保持弦CD的长度不变，那么，直线AD，BC相交所成锐角的大小是否改变? 试就以下三种情况进行探究，并说明理由（图形未画完整，请你根据需要补全）．
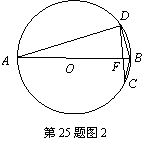① 如图2，弦AB与弦CD交于点F；
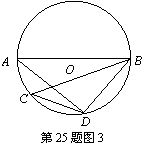② 如图3，弦AB与弦CD不相交；
 |
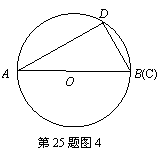③ 如图4，点B与点C重合．