长沙市中考数学试题(毕业)
数 学
本试卷共六道大题,27道小题,满分100分,时间120分钟.
一、填空题(本题共10个小题,每小题2分,满分20分)
1.一2的绝对值为 .
2.因式分解:xy2-x2y= .
3.化简:![]() = .
= .
4.随着工业的发展和人口数量的增加,我国的淡水消耗量逐年增大.据国家统计局《2003年国民经济和社会发展统计公报》发布的数据,2003年我国全年总用水量达万立方米,用科学记数法表示这一数据为 万立方米.
 5.反比例函数y=
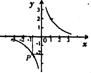
5.反比例函数y=![]() (k≠0)的图像经过点P,如图所示.根据图像可知,反比例函数的解析式为
(k≠0)的图像经过点P,如图所示.根据图像可知,反比例函数的解析式为
![]() 6.如图是一个正方体纸盒的展开图,在其中的四个正方形内标有数字1、2、3和一3.要在其余正方形内分别填上-1、-2,使得按虚线折成正方体后,相对面上的两数互为相反数,则A处应填 .
6.如图是一个正方体纸盒的展开图,在其中的四个正方形内标有数字1、2、3和一3.要在其余正方形内分别填上-1、-2,使得按虚线折成正方体后,相对面上的两数互为相反数,则A处应填 .
7.请用“如果……,那么……”的形式写一个命题:
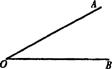
8.∠AOB如图所示,请用直尺和圆规作出∠AOB的平分线(要求保留作图痕迹,不写作法).
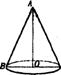 9.已知圆锥的底面半径为2cm,母线长为6cm(如图),则圆锥的侧面展开图的圆心角为
度.
9.已知圆锥的底面半径为2cm,母线长为6cm(如图),则圆锥的侧面展开图的圆心角为
度.
10.探索规律:
31=3,个位数字是3; 32=9,个位数字是9; 33=27,个位数字是7;
34=81,个位数字是1; 35=243,个位数字是3; 36=729,个位数字是9;…那么,37的个位数字是 ,320的个位数字是 .
二,选择题(本题共10个小题,每小题3分.满分30分)
11.下列运算中,正确的是 ( )
A.x2·x3=X6 B.(ab)3=a3b3 C.3a+2a=5 a:D.(a-1)2=a2-1
12.下列一元二次方程中,有实数根的是 ( )
A.x2-x+1=0 B.x2-2x+3=0 C.x2+x-1=0 D.x2+4=0
13.设a=![]() ,则实数a在数轴上对应的点的大致位置是 ( )
,则实数a在数轴上对应的点的大致位置是 ( )
![]()
14.若两圆的半径分别为3cm.5cm,圆心距为2cm,则两圆的位置关系为 ( )
A.外切 B.相交 C.内切 D.内含
15.如图是一个数值转换机,若输入的a值为![]() ,则输出的结果应为 ( )
,则输出的结果应为 ( )
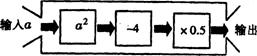
A.2 B.-2 C.1D.-1
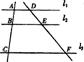 16.如图,已知l1∥l2∥l3,若AB=1,BC=2,DE=1.5,则EF的长为 ( )
16.如图,已知l1∥l2∥l3,若AB=1,BC=2,DE=1.5,则EF的长为 ( )
A.1.5 B. C.2.5 D.3
17.用科学计算器计算锐角a的三角函数值时,不能直接计算出来的三角函数值是 ( )
A.cota B.tana C.cosa D.sina
18.某商店进了一批商品,每件商品的进价为a元,若要获利20%,则每件商品的零售价应定为 ( )
A.20%a(元) B.(1—20%)a(元) C.![]() (元) D.(1+20%)a(元)
(元) D.(1+20%)a(元)
 19.如图,已知MB=ND,∠MBA=∠NDC,下列哪个条件不能判定△ABM≌△CDN ( )
19.如图,已知MB=ND,∠MBA=∠NDC,下列哪个条件不能判定△ABM≌△CDN ( )
A.∠M=∠N B.AB=CD C.AM=CN D.AM∥CN。
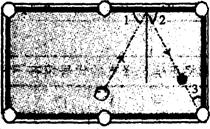
20.如图,∠1=∠2,若∠3=30°,为了使白球反弹后能将黑球直接撞入袋中,那么击打白球时必须保证∠1为 ( )
A.30° B.45° C.60° D.75°
三、(本题共4个小题.每小题5分,满分20分)
21.计算23+2![]() +(6-π)0-
+(6-π)0-![]() .
.
22.解不等式组![]() .
.
![]()
23.某公司员工的月工资如下:
| 员 工 | 经理 | 副经理 | 职员A | 职员B | 职员C | 职员D | 职员E |
| 月工资(元) | 6000 | 3500 | 1500 | 1500 | 1500 | 1100 | 1000 |
(1)该公司员工月工资的中位数是 ,众数是 .
(2)该公司员工月工资的平均数是多少?
(3)用平均数还是用中位数和众数描述该公司员工月工资的一般水平比较恰当?
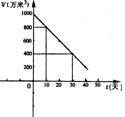
24.2003年夏天,湖南省由于持续高温和连日无雨,水库蓄水量普遍下降.下图是某水库的蓄水量V万米3)与干旱持续时间t(天)
之间的关系图,请根据此图,回答下列问题:
(1)该水库原蓄水量为多少万米3?持续干旱10天后,水库蓄水量为多少万米3?
(2)若水库的蓄水量小于400万米3时,将发出严重干旱警报,请问:持续干旱多少天后,将发生严重干旱警报?
(3)按此规律,持续干旱多少天时,水库将干涸?
四、(本题满分8分)
25.长沙市某公园的门票价格如下表所示:
| 购票人数 | 1~50人 | 51~100人 | 100人以上 |
| 票价 | 10元/人 | 8元,人 | 5元/人 |
某校初三年级甲、乙两个班共100多人去该公园举行毕业联欢活动,其中甲班有50多人,乙班不足50人.如果以班为单位分别买门票,两个班一共应付920元;如果两个班联合起来作为一个团体购票,一共只要付515元.问:甲、乙两班分别有多少人?
五、(本题满分1O分)
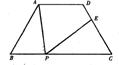
26.如图,等腰梯形ABCD中,AD∥BC,AD=3cm,BC=7cm,∠B=60°,P为下底BC上一点(不与B、C重合),连结AP,过P点作PE交DC于E,使得∠APE=∠B
(1)求证:△ABP∽△PCE;
(2)求等腰梯形的腰AB的长;
(3)在底边BC上是否存在一点P,使得DE:EC=5:3?如果存在,求BP的长;如果不存在,请说明理由.
六、(本题满分12分)
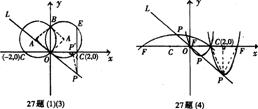
27.已知两点0(O,O)、B(0,2),⊙A过点,B且与x轴分别相交于点O、C,⊙A被y轴分成两段圆弧,其弧长之比为3:1.直线l与⊙A切于点O,抛物线的顶点在直线L上运动.
(1)求⊙A的半径;
(2)若抛物线经过O、C两点,求抛物线的解析式;
(3)过L上一点P的直线与⊙A交于C、E两点,且PC=CE,求点E的坐标;
(4)若抛物线与x轴分别相交于C、F两点,其顶点P的横坐标为m,求△PFC的面积S关于m的函数解析式.
长沙市中考数学试题答案
1.22.xy(y-x)3.![]() 4.5.41×107 5.y=
4.5.41×107 5.y=![]()
6.-27.略8.略9.120 10.7,1
11.B 12.C 13.B 14. C 15.D 16.D 17.A 18.D 19.C 20.C
21.解:原式=5.
22.不等式组的解集为:X>3
![]()
23.解:(1)中位数是1500,众数是1500.
(2)该公司员工资的平均数为:2300(元)
(3)答:用中位数和众数比较恰当.
24.解:(1)水库原蓄水量为1000万米3,持续干旱10天后蓄水量为800万米3.
(2)持续干旱30天后将发出严重干旱警报.
(3)持续干旱50天水库将干涸.
25.甲班有55人,乙班有48人.
26.(1)证明:略.
(2)过A作AF⊥BC于F,由已知易求得BF=2cm.
在Rt△BF中,∠B=60°,BF=2∴AB=4cm.
(3)存在这样的点P,理由如下:
由DE:EC=5:3,DE+EC=DC=4,
得EC=3/2cm.
设BP=x, 则PC=7-x,
由△ABP∽△PCE可得:AB/PC=BP/EC,
x1=1,x2=6.
经检验,都符合题意BP=1cm或BP=6cm.
27.(1)由弧长之比为3:1,可得∠BAO=90°,
再由AB=AO=r,且OB=2,得r=![]() .
.
(2)O A的切线l过原点,可设L为y=kx,
任取L上一点(b,kb),由L与y轴夹角为45°可得:
.b=-kb或b=kb,得k=-1或k=1 直线∠的解析式为y=-x或y=x..
又由r=![]() ,易得C(2,0)或(-2,0).
,易得C(2,0)或(-2,0).
由此可设抛物线解析式为y=ax(x-2)或y=ax(x+2),
再把顶点坐标代入L的解析式中得a=1.
∴抛物线为y=x2-2x或y=x2+2x.
(3)当L的解析式为y=-x时,由p在L上,可设P(m,-m)(m>O)
过P作PP’⊥x轴于P’.OP'=m,PP'=-m OP=2m2,
又由切割线定理可得:OP2=PC·PE,且PC=CE,得PC=CE=m=PP’
∴C与P'为同一点,即PE⊥x轴于C .m=2 E(2,2)
同理,当L的解析式为y=x时,m=-2,E(-2,2).
(4)若C(2,0),此时L为y=-x.∵P与点0、点C不重合.m≠0且m≠2,
当m<O时,FC=2(2-m),高为yp即为-m,
∴.s=m2-2m,
同理当0<m<2时,S=-m2+2m;当m>2时,S=m2-2m;
![]()
又若c(-2,0),此时L为y=x,同理可得:![]()