2006年中考第一轮复习（二）平面直角坐标系、函数概念
基础达标验收卷
一、选择题：
1.
（02江西）在平面直角坐标系中，点
一定在（ ）
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2.
（03黄冈）在平面直角坐标系中，点
在第四象限，则x的取值范围是（ ）
A. 3<x<5 B.
C.
D.
3. （04南京）在平面直角坐标系中，点P（2，1）关于原点对称的点在（ ）
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
4.
（03重庆）三峡大坝从6月1日开始下闸蓄水，如果平均每天流入库区的水量为a立方米，平均每天流出的水量控制为b立方米，当蓄水位低于135米时，
；当蓄水位达到135米时，
. 设库区的蓄水量y（立方米）是时间t（天）的函数，那么这个函数的大致图象是下图中的（ ）
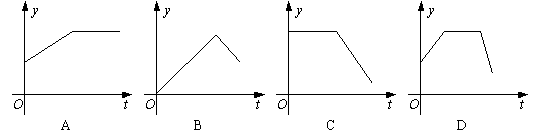
5.
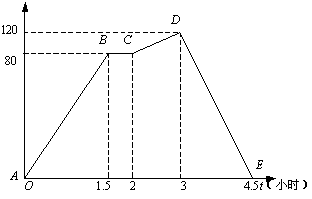（04无锡）如右图中的图象（折线ABCDE）描述了一汽车在某一直路上行驶的过程，汽车离出发地的距离s（千米）和行驶时间t（小时）之间的函数关系，根据图中提供的信息，给出下列说法：①汽车共行驶了120千米；②汽车行驶途中停留了0.5小时；③汽车在每个行驶过程中平均速度为
千米/小时；④汽车在出发后3小时至4.5小时之间行驶速度在逐渐减小，其中正确的说法有（ ）
A. 1个 B. 2个
C. 3个 D. 4个
6.
函数
中自变量x的取值范围是（ ）
A. 
≥0 B.
且x≠1 C.
D.x≥0且x≠1
7.
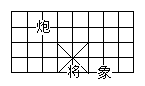如右图，若在象棋盘上建立直角坐标系，使“将”位于点
，“象”位于点
，则“炮”位于点（ ）
A. 
B.
C.
D.
二、填空题：
1.
点
在函数
的图象上，则点A关于y轴对称点的坐标是_____________.
2.
（03上海）已知函数
，那么
=________________.
3. （03寒亭）直角坐标系中，第四象限内的点M到x轴、y轴的距离分别为3，2，则M点的坐标是________________.
4.
函数
中，自变量x的取值范围是_____________________.
5.
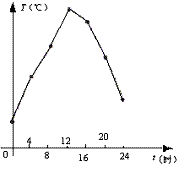（04宜昌）如右图，是某生物实验室的温度自动描点记录仪所录绘该室2004年4月8日的气温随时间变化的图象. 请你结合下表观察图象记录中的7个点，大致估计表中缺失的数据并补写出来：________.
|
6.
（05云南）函数
中，自变量x的取值范围是_______________.
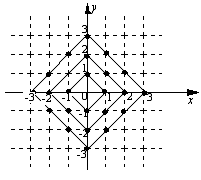
7. 在平面直角坐标系中，横坐标、纵坐标都是整数的点称为整点. 观察图中每一个正方形（实线）四条边上的整点的个数，请你猜测由里向外第10个正方形（实线）四条边上的整点个数共有___________个.
三、解答题：
1. （03武汉）小强在劳动技术课中要制作一个周长为80cm的等腰三角形，请你写出底边长y（cm）与一腰长x（cm）的函数关系式，并求出自变量x的取值范围.
2. （03南宁）南宁市某中学环保兴趣小组对南胡清除淤泥工程进行调查，并从《南宁晚报》上收集到下列数据：
| 南胡面积（单位：米2） | 淤泥平均厚度（单位：米） | 每天清淤泥量（米3） |
| 160万 | 0.7 | 0.6万 |
根据上表解答下列问题：
（1）请你按体积=面积×高来估算，南胡的淤泥量大约有多少万立方米？
（2）设清除淤泥x天后，剩余的淤泥量为y（万米3），求y与x的函数关系（不要求写出自变量x的取值范围）.
（3）为了使南胡的生物链不遭到破坏，仍需保留一定量的淤泥. 若需保留的淤泥量约为22万米3，求清除淤泥所需天数.
3.
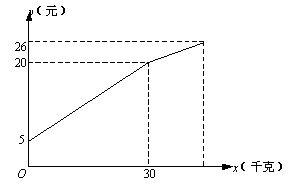（02吉林）一农民带了若干千克自产的土豆进城出售，为了方便，他带了一些零钱备用，按市场价售出一些后，又降价出售. 售出土豆千克数与他手持有的钱数（含备用零钱）的关系如右图所示，结合图象回答下列问题：
（1）农民自带的零钱是多少？
（2）降价前他每千克土豆出售的价格是多少？
（3）降价后他按每千克0.4元将剩余土豆售完，这时他手中的钱（含备用零钱）是26元，问他一共带了多少千克土豆？
能力提高练习
一、学科内综合题
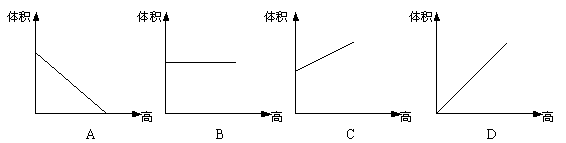
1. （04柳州）如右图，将一个“瘦长”的圆柱钢锭经过多次锻压成一个“矮胖”的圆柱钢锭（不计损耗），则在锻压过程中，圆柱体积与高的关系可用图象（如下图）表示的是（ ）
2.
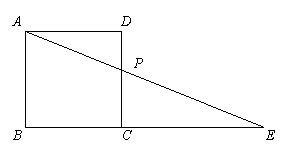（02聊城）如右图，正方形ABCD的边长为2cm，P是边CD上一点，连结AP并延长与BC的延长线交于点E. 当点P在边CD上移动时，△ABE的面积随之变化.
（1）设PD=xcm（0<x≤2），求△ABE的面积y与x的函数关系式，并画出函数的图象；
（2）根据（1）中的函数关系式，确定点P在什么位置时S△ABE=400cm2？
二、开放探索题
3. （03黄冈）同学们都做过《代数》课本第三册第87页第4题：某礼堂共有25排座位，第一排有20个座位，后面每一排比前一排多1个座位，写出每排的座位数m与这排的排数n的函数关系式并写出自变量n的取值范围.
上题中，在其他条件不变的情况下，请探究下列问题：
（1）当后面每一排都比前一排多2个座位时，则每排的座位数m与这排的排数n的函数关系式是______________（1≤n≤25，且n是整数）.
（2）当后面每一排都比前一排多3个座位、4个座位时，则每排的座位数m与这排的排数n的函数关系式是______________（1≤n≤25，且n是整数）.
（3）某礼堂共有p排座位，第一排有a个座位，后面每一排比前一排多b个座位，试写出每排的座位数m与这排的排数n的函数关系式并指出自变量n的取值范围.
三、实际应用题
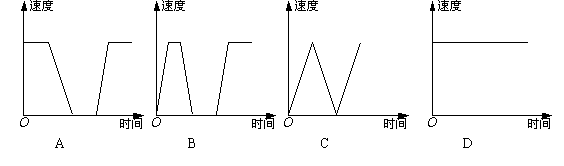
4. （03青岛）一列火车从青岛出发，加速行驶一段时间后开始匀速行驶. 过了一段时间，火车到了下一个车站. 乘客上下车后，火车又加速，一段时间后再次开始匀速行驶，下图中的（ ）可以近似地刻画出火车在这段时间内的速度变化情况.
5. （03大连）阅读下列材料：
“父亲和儿子同时去晨练，如图（1），实线表示父亲离家的路程y（米）与 时间x（分钟）的函数图象；虚线表示儿子离家的路程y（米）与时间x（分钟）的函数图象. 由图象可知，，他们在出发10分钟时第一次相遇，此时离家400米；晨练了30分钟，他们同时回到家.”
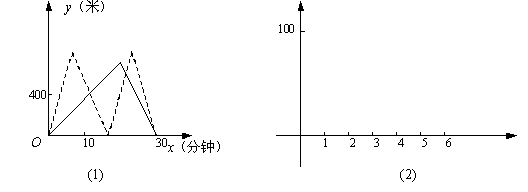
根据阅读材料给你的启示，利用指定的直角坐标系（图（2））或用其他方法解答下列问题：
一巡逻艇和一货轮同时从A港口前往相距100千米的B港口，巡逻艇和货轮的速度分别为100千米/时和20千米/时，巡逻艇不停地往返于A、B两港口（巡逻艇调头的时间不计）.
（1）货轮从A港口出发以后直到B港口与巡逻艇一共相遇了几次？
（2）出发多少时间巡逻艇与货轮第三次相遇？此时离A港口多少千米？
四、跨学科综合题
6.
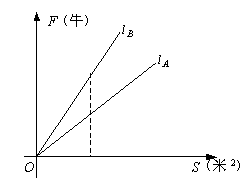（02辽宁）两个物体A、B所手压强分别为
（帕）与
（帕）（、为常数），它们所受压力F（牛）与受力面积S（米2）的函数关系图象分别是射线
、
，如右图所示，则（ ）
A. 
B.
C. 
D.
≤
参考答案
基础达标验收卷
一、选择题：
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 答案 | B | A | C | A | A | D | B |
二、填空题：
1. 
2.
3.
4.
x≥
且x≠2
5. 答案在19.9~22之间（不包括19.9和22）均可 6.
7.
40
三、解答题：
1. 解：
.
∵
，∴
. ∴自变量x的取值范围是
.
2. 解：（1）160×0.7=112（万米3）；
（2）
；
（3）当
时，
. 解得
（天）
答：需要150天.
3. 解：（1）农民自带的零钱是5元.
（2）
（元）.
答：降价前他每千克土豆卖0.5元.
（3）
（千克）.
答：他一共带了45千克土豆.
能力提高练习
1. B
2. 解：（1）
（0<x≤2）图略.
（2）当PD=0.01cm时，S△ABE=4002.
3. 解：每排的座位数m与这排的排数n的函数发现式是
；
自变量n的取值范围是1≤n≤25.
（1）
；
（2）
，
；
（3）
自变量n的取值范围是1≤n≤p.
4. B
5. 解：（1）由题意可画图象如下图.
∴货轮从A港口出发以后直到B港口与巡逻艇一共相遇4次.
（2）设OC所在的直线为
.
∵过点
，∴
，∴
. ∴
.
设EF所在的直线为
.
∵过点
，
，∴
解得
∴
.
由
解得
答：出发
小时巡逻艇与货轮第三次相遇，这时离A港口
千米.