2006年中考第一轮复习（四）反比例函数
基础达标验收卷
一、选择题：
1.
（03北京海淀区）已知反比例函数
的图象经过点
，则函数
可确定为（ ）
A. 
B.
C.
D.
2.
（04太原）如果反比例函数的图象经过点
，那么下列各点在此函数图象上的是（ ）
A. 
B.
C.
D.
3.
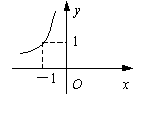（03广东）如右图，某个反比例函数的图象经过点P，则它的解析式为（ ）
A. 
B.
C. 
D.
4.
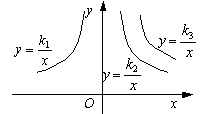（04河南）如右图是三个反比例函数
，
，
在x轴上方的图象，由此观察得到
、
、
的大小关系为（ ）
A. 
B.
C. 
D.
5.
（03广西）已知反比例函数
的图象上有两点
、
且
，那么下列结论正确的是（ ）
A. 
B.
C.
与
之间的大小关系不能确定
6.
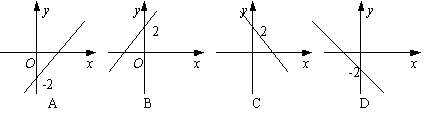（03汕头）已知反比例函数的图象如右图，则函数
的图象是下图中的（ ）
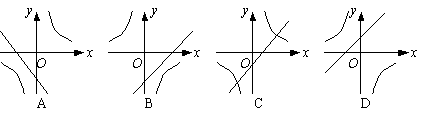
7.
已知关于x的函数
和
（k≠0），它们在同一坐标系内的图象大致是（ ）
8.
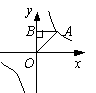
（05吉林）如图，点A是反比例函数
图象上一点，AB⊥y轴于点B，则△AOB的面积是（ ）
A. 1 B. 2 C. 3 D. 4
9.
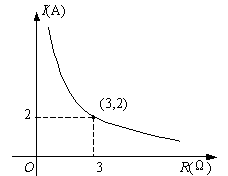（05河北）某闭合电路中，电源的电压为定值，电流I（A）与电阻R（Ω）成反比例. 右图表示的是该电路中电流I与电阻R之间的图象，则用电阻R表示电流I的函数解析式为（ ）
A. 
B.
C. 
D.
二、填空题：
1.
（04北京）我们学习过反比例函数.
例如，当矩形面积S一定时，长a是宽b的反比例函数，其函数关系式可以写为
（S为常数，S≠0）.
请你仿照上例另举一个在日常生活、生产或学习中具有反比例函数关系的量的实例，并写出它的函数关系式.
实例：_________________________________________________；
函数关系式：___________________________________________.
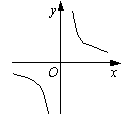
2.
（03南宁）右图是反比例函数的图象，那么k与0的大小关系是
.
3.
（03吉林）点
在双曲线上，则k=______________.
4. （03安徽）近视眼镜的度数y（度）与镜片焦距x（米）成反比例. 已知400度近视眼镜镜片的焦距为0.25米，则眼镜度数y与镜片焦距x之间的函数关系式是_____________.
5.
（05海南）已知反比例函数
的图象经过点
，则a=__________.
三、解答题：
1.
（03甘肃）已知一次函数
的图象与反比例函数
的图象在第一象限交于点
，求k，n的值.
2.
（03镇江）已知反比例函数的图象与一次函数
的图象相交于点
.
（1）分别求这两个函数的解析式.
（2）试判断点
关于x轴的对称点
是否在一次函数的图象上.
3.
（04大连）反比例函数的图象经过点
.
（1）求这个函数的解析式；
（2）请判断点
是否在这个反比例函数的图象上，并说明理由.
4.
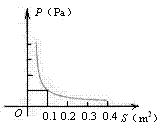（04南京）在压力不变的情况下，某物承受的压强P（Pa）是它的受力面积S（m2）的反比例函数，其图象如右图所示.
（1）求P与S之间的函数关系式；
（2）求当S=0.5m2时物体所受的压强P.
5.
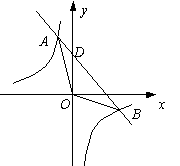（05甘肃）如图，反比例函数与一次函数
的图象交于A、B两点.
（1）求A、B两点的坐标；
（2）求△AOB的面积.
能力提高练习
一、学科内综合题
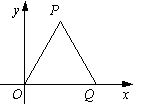
1. 如右图，△OPQ是边长为2的等边三角形，若反比例函数的图象过点P，则它的解析式是_____________.
2.
（04四川）已知反比例函数
和一次函数
.
（1）若一函数和反比例函数的图象交于点
，求m和k的值.
（2）当k满足什么条件时，这两个函数的图象有两个不同的交点？
（3）当
时，设（2）中的两个函数图象的交点分别为A、B，试判断A、B两点分别在第几象限？∠AOB是锐角还是钝角（只要求直接写出结论）？
二、学科间综合题
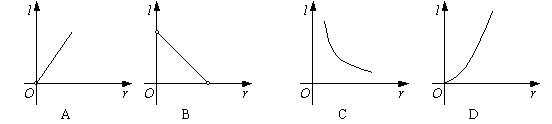
3. （03连云港）若一个圆锥的侧面积为20，则下图中表示这个圆锥母线长l与底面半径r之间函数关系的是（ ）
三、实际应用题
4.
某单位为响应政府发出的全民健身的号召，打算在长和宽分别为20米和11米的矩形大厅内修建一个60平方米的矩形健身房ABCD. 该健身房的四面墙壁中有两侧沿用大厅的旧墙壁（如图为平面示意图），已知装修旧墙壁的费用为20元/平方米，新建（含装修）墙壁的费用为80元/平方米. 设健身房的高为3米，一面旧墙壁AB的长为x米，修建健身房的总投入为y元.
（1）求y与x的函数关系式；
（2）为了合理利用大厅，要求自变量x必须满足8≤x≤12. 当投入资金为4800元时，问利用旧墙壁的总长度为多少米？
5.
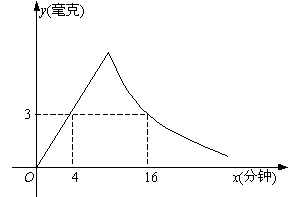
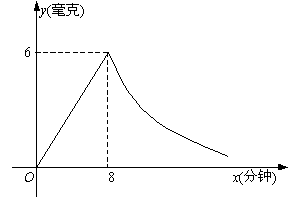（03金华）为了预防“非典”，某学校对教室采用药熏消毒法进行消毒. 已知药物燃烧时，室内每立方米空气中的含药量y（毫克）与时间x分钟）成正比例，药物燃烧完后，y与x成反比例（如图所示）. 现测得药物8分钟燃毕，此时室内空气中每立方米含药量为6毫克. 请根据题中所提供的信息，解答下列问题：
（1）药物燃烧时，y关于x的函数关系式为：___________________，自变量x的取值范围是：______________；药物燃烧后y关于x的函数关系式为：___________________；
（2）研究表明，当空气中每立方米的含药量低于1.6毫克时学生方可进教室，那么从消毒开始，至少需要经过几分钟后，学生才能回到教室；
（3）研究表明，当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时，才能有效地杀灭空气中的病菌，那么此次消毒是否有效？为什么？
参考答案
基础达标验收卷
一、选择题：
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 答案 | A | B | D | B | D | D | B | B | C |
二、填空题：
1. 当路程s一定时，速度v是时间t的反比例函数；
（s是常数，s≠0）
2. > 3.
6 4.
5.
三、解答题：
1. 解：∵在反比例函数
的图象上，∴
.
又∵
在一次函数的图象上，∴
，
.
∴k，n的值分别为
，2.
2. 解：（1）由题意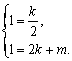得
解得
∴反比例函数为
，一次函数为
.
（2）∵
，∴
把
代入，得
.
∴不在一次函数的图象上.
3. 解：（1）由题意得
，∴
.
∴函数解析式为
.
（2）当
时，
.
∴点（1，6）在这个反比例函数的图象上.
4. 解：（1）设
，∵点（0.1，1000）在这个函数的图象上，
∴
. ∴k=100.
∴p与S的函数关系式为
.
（2）当S=0.5m2时，
（Pa）.
5. 解：（1）解方程组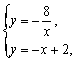
得
∴A、B两点的坐标分别为
、
.
（2）∵直线与y轴交点D的坐标是（0，2），
∴S△AOD=
，S△BOD=
.
∴S△AOB=2+4=6.
能力提高练习
1. 
（x>0）
2. 解：（1）
，
.
（2）当
且k≠0时，这两个函数的图象有两个不同的交点.
（3）当时，
在k的可取值范围内，此时函数
的图象在第二、四象限内，从而它与
的两个不同交点在第二、四象限内，此时∠AOB是钝角.
3. C
4. 解：（1）根据题意，AB=x，AB·BC=60，所以
.
，即
.
（2）当y=4800时，有
.
去分母并整理，得
.
解得
，
.
经检验，，都是原方程的根.
由8≤x≤12，只取x=10.
所以利用旧墙壁的总长度为
米.
5. 解：（1）
，0<x≤8（或0≤x≤8或0<x<8或0≤x<8亦可）；
.
（2）30.
（3）此次消毒有效. 把
代入，得
；把代入，得
.
∵
，即空气中含药量不低于3毫克/米3的持续时间为12分钟，大于10分钟的有效杀毒时间（如下图所示），所以消毒有效.
