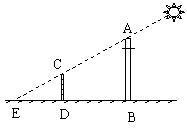三十九中学2006年中考数学复习检测（5）（圆、视图与投影）
姓名 得分
一、选择题（每小题3分，共30分）
1．小明从正面观察下图所示的两个物体，看到的是 （ ）
 |
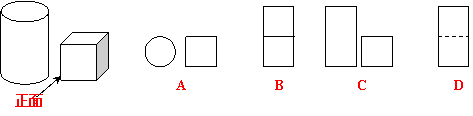2．在同一时刻，身高1.6m的小强的影长是1.2m，旗杆的影长是15m，则旗杆高为 （ ）
A、16m B、18m C、20m D、22m
3. 已知⊙
的半径为3cm，圆心到直线
的距离为2cm，则直线与⊙的位置关系为
Ａ．相离 Ｂ．外切 Ｃ．相交 Ｄ．内切 （ ）
4. 已知⊙1与⊙2 相切，半径分别为
和
，则两圆的圆心距为 （ ）．
Ａ．
Ｂ．
Ｃ．或 Ｄ．
或
5．下列命题正确的是 （ ）．
Ａ．垂直于直径的直线是圆的切线
Ｂ．平分弧的直径垂直于弦，并且平分弦所对的弧
Ｃ．三点确定一个圆
Ｄ．在同圆或等圆中，同弧或等弧所对的圆周角相等
6. 
、
、
是平面内的三点，
，
，
，下列说法正确的是（ ）
Ａ．可以画一个圆，使、、都在圆上
Ｂ．可以画一个圆，使、在圆上，在圆外
Ｃ．可以画一个圆，使、在圆上，在圆外
Ｄ．可以画一个圆，使、在圆上，在圆内
7.已知⊙O的半径为2cm,弦AB长为
cm,则这条弦的中点到弦所对劣弧的中点的距离为
A 1 B 2 C 3 D 4 ( )
8．如图，将半径为2的圆形纸片，沿半径
，
将其截成
面积为
两部分，将所得的扇形OAB围成圆锥的侧面，
则圆锥的底面半径为（ ）
Ａ．
Ｂ．1 Ｃ．1或3
Ｄ．或
9．如图，在△
中，
，
，若以
为底面圆半径、
为高的圆锥的侧面积为
，以为底面圆半径、为高的圆锥的侧面积为
，
则（ ）．
Ａ．
Ｂ．
Ｃ．
Ｄ．，的大小关系不确定
10.如图，扇形
的圆心角为
，且半径为
，分别以
，为直径在扇形内作半圆，
和
分别表示两个
阴影部分的面积，那么和的大小关系是（ ）
Ａ.
Ｂ．
Ｃ．
Ｄ．无法确定
二、填空题（每空2分，共22分）
|
|
11、如图，一几何体的三视图如右：
那么这个几何体是 ；
12．小明希望测量出电线杆AB的高度，于是在阳光明媚的一天，他在电线杆旁的点D处立一标杆CD，使标杆的
影子DE与电线杆的影子BE部分重叠（即点E、C、A在
一直线上），量得ED＝2米，DB＝4米，CD＝1.5米，则
电线杆AB长＝
13．已知圆的面积为
，若其圆周上一段弧长为
，则这段弧所对的圆心角的度数为 ．
14. 如图2，
内接于⊙O，
，
。则⊙O半径的长为 。
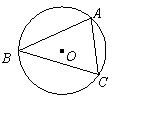
15．如图3，点Ａ、B、C在⊙O上，∠AOB=130°，则∠C=_________度,∠D=_________度；
16．如图4，在两个同心圆中，三条直径把大圆分成相等的六部分，若大圆的半径为2，则图中阴影部分的面积为 ．
 | |||
 | |||
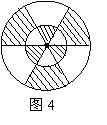图2 图3
17．圆锥的母线长5cm，底面半径长3cm，那么它的侧面展开图的圆心角是 。
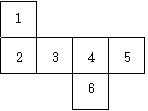18．右图是一个正方体的表面展开图，将它折叠可得一正方体，
这个正方体的3号侧面所对的侧面是______________．
 | |||
 | |||
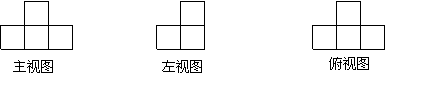19．上图是由一些相同的小正方体构成的几何体的三视图，在这个几何体中，小正方体的个数是 。
20．如图，两个半径为1，圆心角是的扇形和扇形
叠放在一起，点
在弧AB上，四边形
是正方
形，则阴影部分的面积等于 ．
三、画图题（每小题6分，共12分）
21.画出下列图形三视图
 |
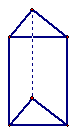22．图为一块圆形砂轮破碎后的部分残片，试找出它的圆心．
四、计算与证明（每小题8分，共16分）
23．如图，⊙O的直径
和弦
相交于点
，已知
，
，
，求的长．
 |
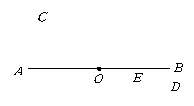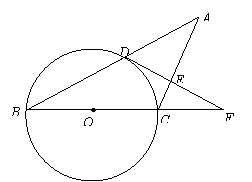24．已知：如图，△中，
，以为直径的
交于点
，过点作
于点，交的延长线于点
．
求证：（1）
；
（2）
是的切线．
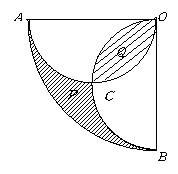
五、探究与思考（每小题10分，共20分）
25．某公司临街面的外墙上有一块三角形的墙面发生破损现象（如图所示△即是），公司领导让工人师傅做一个圆形广告牌，将破损面全部覆盖住，工人师傅量得
，
，
．为使所做广告牌最小，工人师傅给出两种方案：
（1）
作△的外接圆；（2）以为直径作圆．
哪个方案中的圆面积最小？是多少？
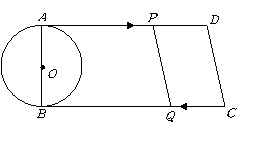26.如图，在直角梯形
中，
，
，
，
，
，为⊙O的直径，动点从点开始沿
边向点以
的速度运动，动点从点开始沿
向点以
的速度运动，并且，分别从点，同时出发，当其中一点到达端点时，另一点也随之停止运动．设运动时间为
，则
分别为何值时，直线
与⊙O相切、相交和相离？