扬州中考全真模拟试卷(5)华师大版

2006年中考全真模拟试卷（五）

（时间120分钟，满分150分）

一、选择题 （每题3分，共36分.每小题有四个选项，其中只有一个选项是正确的，将正确选项的字母填入下表相应的题号下面.）  

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案

1、今年2月3日我市最低气温为-6℃，最高气温为7℃，那么这一天最高气温比最低气温高(　　)

A．7℃　　　 B．13℃　　　　　　C．1℃　　　　　D．-13℃

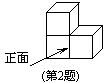
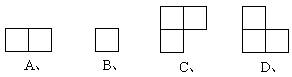
2、如右图，由三个小立方体搭成的几何体的俯视图是（　　  ）　

3、下列运算正确的是（　　  ）

A．　 B．　　　C．　 D．

4、生物学统计，一个健康的女子体内每毫升血液中红细胞的数量约为420万个，用科学计数可表示为（　　　　  ）个

Ａ．　　  B．　　C．　　 D．

5、若反比例函数的图象经过点A（2，m），则m的值是（　　 ）

　　A. 　　　　　B. 　　　　　　 　C. 　　　　　　  D.

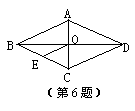
6、已知：如图,菱形ABCD中,对角线AC与BD相交于点O,

OE∥DC交BC于点E,AD=6cm,则OE的长为 （　　　　）

A、6 cm　　　　　　　 B、5 cm　　　　　　　

C、4 cm　　　　　　　 D、3 cm

7、有一对酷爱运动的年轻夫妇给他们12个月大的婴儿拼排3块分别写有“20”，“08”，和“北京”的字块，如果婴儿能够排成“2008北京”或者“北京2008”，则他们就 给婴儿奖励，假设该婴儿能将字块横着正排，那么这个婴儿能得到奖励的概率是（　）

（A）　　  （B）　　　（C） 　　 （D） 

8、一列货运火车从扬州站出发，匀加速行驶一段时间后开始匀速行驶，过了一段时间，火车到达下一个车站停下，装完货以后，火车又匀加速行驶，一段时间后再次开始匀速行驶，可以近似地刻画出火车在这段时间内的速度变化情况的是（　　）

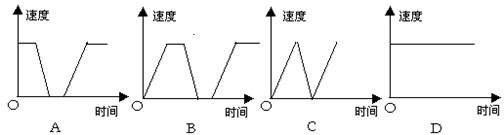9、如图，将一张正方形纸片经两次对折，并剪出一个菱形小洞后展开铺平，得到的图形是（　　）

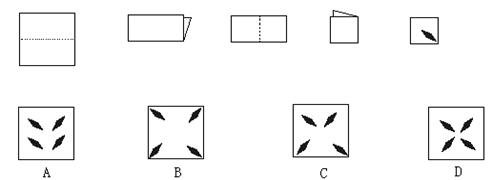
10、如图，圆锥的母线长是3，底面半径是1，A是底面圆周上一点，从点A出发绕侧面一周，再回到点A的最短的路线长是（　　　 ）　

A、　　  B、　　C、　　　 D、3

　　　　 

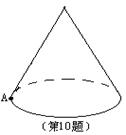
11、如图，点P是⊙O的直径BA延长线上一点，PC与⊙O相切于点C，CD⊥AB，垂足为D，连结AC、BC、OC，那么下列结论中，①PC²=PA·PB ； ②PC·OC=OP·CD ；③OA²=OD·OP；④OA（CP－CD）=AP·CD。正确的结论有（　　　 ）个。

　　（A）、4　　　　（B）、3　　　 （C）、2　　　　（D）、1

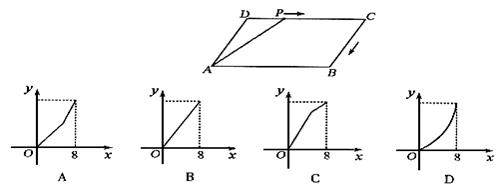
12、 如下图，在平行四边形ABCD中，∠DAB＝60°，AB＝5，BC＝3，点P从起点D出发，沿DC、CB向终点B匀速运动。设点P所走过的路程为x，点P所经过的线段与线段AD、AP所围成图形的面积为y，y随x的变化而变化。在下列图象中，能正确反映y与x的函数关系的是（　　）

二、填空题：(每题4分，共24分)

13、 函数的自变量x的取值范围是_______________.

14、用换元法解方程，那么原方程可变形为 　　　　　　　　 。

15、如图，AB＝AC ，要使，应添加的

条件是_______　 _____　　　 (添加一个条件即可)。

16、若正比例函数y ＝kx与y＝2x的图象关于x轴对称，

　 则k的等于___________

17. 在△ABC中，∠B＝25°，AD是BC边上的高，并且，则∠BCA的度数为______　　 ______。

18、如下图所示，按下列方法将数轴的正半轴绕在一个圆上（该圆周长为3个单位长，且在圆周的三等分点处分别标上了数字0、1、2）上：先让原点与圆周上0所对应的点重合，再将正半轴按顺时针方向绕在该圆周上，使数轴上1、2、3、4、…所对应的点分别与圆周上1、2、0、1、…所对应的点重合。这样，正半轴上的整数就与圆周上的数字建立了一种对应关系。若数轴上的一个整数点刚刚绕过圆周n圈（n为正整数）后，并落在圆周上数字1所对应的位置，这个整数是______　　 ___（用含n的代数式表示）。

三、解答题 ：(本大题共8题，计90分)

19、（本题满分8分）某校初三（2）班40名同学为“希望工程”捐款,共捐款100元. 班长把捐款情况记入如下的表格中：

捐款（元）	1	2	3	4
人　 数	6			7

但表格中捐款2元和3元的人数不小心被墨水污染已看不清楚.请你帮助班长求出捐款2元和3元的人数？　

 

 

 

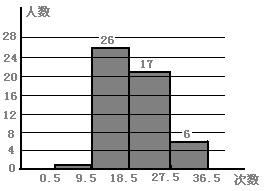
20.（本题满分12分）某市实行中考改革，需要根据该市中学生体能的实际状况重新制定中考体育标准. 为此抽取了50名初中毕业的女学生进行一分钟仰卧起坐次数测试，测试情况绘制成表格及频数分布直方图如下：

次数	6	12	15	18	20	25	27	30	32	35	36
人数	1	1	7	18	10	5	2	2	1	1	2

（1）求这次抽样测试数据的平均数、众数和中位数；

（2）根据这一样本数据的特点，你认为该市中考女生一分钟仰卧起坐项目测试的合格标准次数应定为多少次较为合适？简要说明理由；

（3）根据频数分布直方图，求0.5-9.5组的频率；

（4）如果该市今年有3万名初中毕业女生参加体育中考，根据（2）中你认为合格的标准，试估计该市中考女生一分钟仰卧起坐项目测试的合格人数是多少？

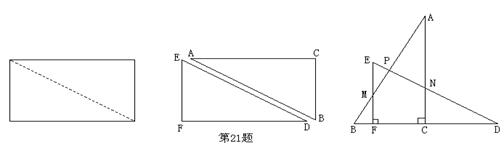
21、（本题10分）

一张矩形纸片沿对角线剪开，得到两张三角形纸片，再将这两张三角形纸片摆成如下右图形式，使点B、F、C、D在同一条直线上。

（1）求证AB⊥ED；

（2）若PB=BC，请找出图中与此条件有关的一对全等三角形，并给予证明。

22、（本题12分）你喜欢玩游戏吗？现请你玩一个转盘游戏，如图所示的两个转盘中指针落在每一个数字上的机会均等，现同时自由转动甲、乙两个转盘，转盘停止后，指针各指向一个数字，用所指的两个数字作乘积。

请你：（1）列举（用列表或画树状图）所有可能得到的数字之积。

（2）求出数字之积为奇数的概率。

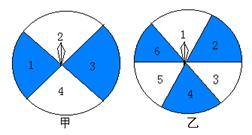
23 、（本题满分12分）一艘渔船在A处观测到东北方向有一小岛C，已知小岛C周围4.8海里范围内是水产养殖场.渔船沿北偏东30°方向航行10海里到达B处，在B处测得小岛C在北偏东60°方向，这时渔船改变航线向正东(即BD)方向航行，这艘渔船是否有进入养殖场的危险？

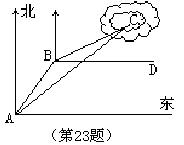
24、（本题满分12分）某人计划购买一套没有装修的门市房，它的地图图形是正方形，若正方形的边长为x米，则办理产权费需1000x元，装修费用y₁(元)与x（米）函数关系式如图所示。

（1）　　　 求y₁ 与x 函数关系式；

（2）　　　 装修后将此门市房出租，租期5年，租金以每年每平方米200元计算。

①求5年到期时，由此门市房所获利润y（元）与x（米）的函数关系式；

②若5年到期时，按计划他将由此门市房获取利润70 000元，求此门市房的面积。（利润=租金－办理产权费用与装修费用之和）

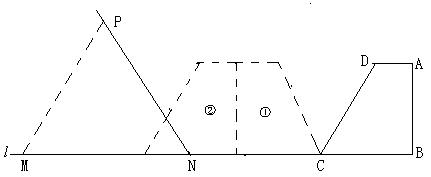
25、（本题12分）

已知，如图，在直角梯形ABCD，AD∥ BC，BC=5cm，CD=6cm，∠DCB=60^O，∠ABC=90^O。等边三角形△MPN（N为不动点）的边长为acm，边MN和直角梯形ABCD的底边BC都在直线 上，NC=8cm，将直角梯形ABCD向左翻折180^O，翻折一次得到图形①，翻折二次得到图形②，如此翻折下去。

（1）　　　 将直角梯形ABCD向左翻折二次，如果此时等边三角形的边长a≥2cm，这时两图形重叠部分的面积是多少？

（2）　　　 将直角梯形ABCD向左翻折三次，如果第三次翻折得到的直角梯形与等边三角形重叠部分的面积等于直角梯形ABCD的面积，这时等边三角形的边长a至少应为多少 ？

（3）　　　 将直角梯形ABCD向左翻折三次，如果第三次翻折得到的直角梯形与等边三角形重叠部分的面积等于直角梯形ABCD的面积的一半，这时等边三角形的边长a 应为多少 ？

　

26、（本题14分）

已知：在平面直角坐标系xOy中，一次函数的图象与x轴交于点A，抛物线经过O、A两点。

　　（1）试用含a的代数式表示b；

　　（2）设抛物线的顶点为D，以D为圆心，DA为半径的圆被x轴分为劣弧和优弧两部分。若将劣弧沿x轴翻折，翻折后的劣弧落在⊙D内，它所在的圆恰与OD相切，求⊙D半径的长及抛物线的解析式；

　　（3）设点B是满足（2）中条件的优弧上的一个动点，抛物线在x轴上方的部分上是否存在这样的点P，使得？若存在，求出点P的坐标；若不存在，请说明理由。

2006年中考全真模拟试卷（五）参考答案

一、选择题 ：

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案	B	A	C	C	C	D	C	B	D	C	A	A

二、填空题：

13、x≤，且x≠-1；

14、；

15、AE=AD或∠B=∠C或∠AEB=∠ADC；

16、－2；

17、65°或115°

18、3n+1

三、解答题

19、解 ：设捐款2元的有名同学,捐款3元的有名同学,根据题意,可得方程组

　　　　解这个方程组得　

答：捐款2元的有 15名同学,捐款3元的有12 名同学,

20、（1）平均数=20.5, 众数=18, 中位数=18　　　

（2）合格标准的次数应定为18次较为合适，因为18既为众数也为中位数，且大部份的初中毕业女生都能达到.　　　　　　　　　　　　 

（3）0.5-9.5组的频率=(50-26-17-6)/50=0.02　

（4）合格人数=30000×41/50=24600　　　　

21、（1）略解：∠由矩形的性质可知：Rt△ABC ≌Rt△DEF，AC⊥BD，EF⊥BD。

∵∠A=∠D ，∠ANP=∠DNC

又∵∠D+∠DNC=90^O

∴∠A+∠ANP=90^O

∴AB⊥ED。

（2）如：△APN ≌△DCN

理由：∵Rt△ABC ≌Rt△DEF

∴AB=BD

又∵PB=BC

∴AP=DC

∴在△APN和△DCN中，

 

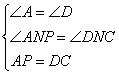
∴ △APN ≌△DCN

22、（1）用列表法来表示所得到的数字之积。

 

乙 甲	1	2	3	4	5	6
1	1×1=1	2×1=2	3×1=3	4×1=4	5×1=5	6×1=6
2	1×2=2	2×2=4	3×2=6	4×2=8	5×2=10	6×2=12
3	1×3=3	2×3=6	3×3=9	4×3=12	5×3=15	6×3=18
4	1×4=4	2×4=8	3×4=12	4×4=16	5×4=20	6×4=24

（2）由上表可知，两数之积的情况有24种，所以P（数字之积为奇数）=

23、解法一：过点B作BM⊥AH于M，∴BM∥AF.∴∠ABM=∠BAF=30°.

　　　　　在△BAM中，AM=AB=5，BM=5.　　

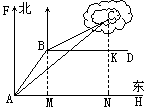　　　　　过点C作CN⊥AH于N，交BD于K.

　　　　　在Rt△BCK中，∠CBK=90°-60°=30°

　　　　　设CK=x，则BK=x.　

　　　　　在Rt△ACN中，∵∠CAN=90°-45°=45°，

　　　　　∴AN=NC.∴AM+MN=CK+KN.

　　　　 又NM=BK，BM=KN.

　　　　　∴x+5=5+x.解得x=5.　

　　　　 ∵5海里＞4.8海里，∴渔船没有进入养殖场的危险.　

　　　　　　　 答：这艘渔船没有进入养殖场危险.　　

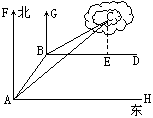　　 解法二：过点C作CE⊥BD，垂足为E，∴CE∥GB∥FA.

　　　　　　∴∠BCE=∠GBC=60°.∠ACE=∠FAC=45°.

　　　　　　∴∠BCA=∠BCE-∠ACE=60°-45°=15°.

　　　　　　又∠BAC=∠FAC-∠FAB=45°-30°=15°，

　　　　　　∴∠BCA=∠BAC.∴BC=AB=10.

　　　　　　在Rt△BCE中，CE=BC·cos∠BCE=BC·cos60°=10×=5(海里).

　　　　　　∵5海里＞4.8海里，∴渔船没有进入养殖场的危险.

　　　　　　答：这艘渔船没有进入养殖场的危险.

24、解：（1）设y₁ 与x 函数关系式为y₁=kx，

　　　　把（1，2000）代入上式得k=2000，

　　　　所以y₁ 与x 函数关系式为y₁=2000x，

　　 （2）①y与x的函数关系式为

②当y=70000时，70000=，

整理得：

解得：。故门市房的面积需要100平方米。

25、解（1）重叠部分面积等于；

（2）等边三角形的边长a至少应为10cm；

（3）等边三角形的边长为。

26、（1）解法一：∵一次函数的图象与x轴交于点A

　　 ∴点A的坐标为（4，0）

　　∵抛物线经过O、A两点

　　

　　 

　　解法二：∵一次函数的图象与x轴交于点A

　　∴点A的坐标为（4，0）

　　∵抛物线经过O、A两点

　　∴抛物线的对称轴为直线

　　

　　 

　　（2）解：由抛物线的对称性可知，DO＝DA

　　∴点O在⊙D上，且∠DOA＝∠DAO

　　又由（1）知抛物线的解析式为

　　∴点D的坐标为（）

　　①当时，

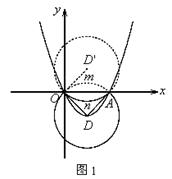
　　如图1，设⊙D被x轴分得的劣弧为，它沿x轴翻折后所得劣弧为，显然所在的圆与⊙D关于x轴对称，设它的圆心为D'

　　∴点D'与点D也关于x轴对称

　　∵点O在⊙D'上，且⊙D与⊙D'相切

　　∴点O为切点

　　∴D'O⊥OD

　　∴∠DOA＝∠D'OA＝45°

　　∴△ADO为等腰直角三角形

　　 

　　∴点D的纵坐标为

　　

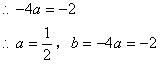
　　∴抛物线的解析式为

　　②当时，

　　同理可得：

　　抛物线的解析式为

　　综上，⊙D半径的长为，抛物线的解析式为或

　　（3）解答：抛物线在x轴上方的部分上存在点P，使得

　　设点P的坐标为（x，y），且y＞0

　　①当点P在抛物线上时（如图2）

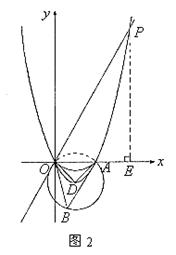
　　∵点B是⊙D的优弧上的一点

　　

　　

　　过点P作PE⊥x轴于点E

　　

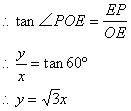
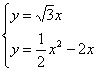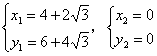　　由解得：（舍去）

　　∴点P的坐标为

　　②当点P在抛物线上时（如图3）

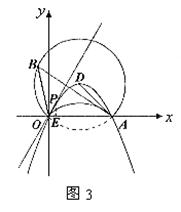
　　同理可得，

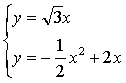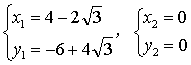　　由解得：（舍去）

　　∴点P的坐标为

　　综上，存在满足条件的点P，点P的坐标为

　  或