2006年初三数学中考模拟测试题 (E.)
本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分;试卷共4页(另有答题卷4页)共150分。考试时间为120分钟。
第Ⅰ卷 (选择题,共33分)
注意事项:
1. 答第Ⅰ卷前,考生必须将自己的姓名、考生号、考试科目等用铅笔填涂在答题卡上。
2. 每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需要改动,用橡皮擦干净后,再选涂其它答案。不能答在试题卷上。
一、选择答案:(本题共11小题,每小题3分,共33分)
注意:每小题有四个选项,其中有且仅有一项是符合题意的,所有选择题必须在答题卡上用规定的铅笔作答,选错、不选、多选或涂改不清的,均不给分.
1.我国最长的河流长江全长约6300千米,用科学记数法表示为( )千米.
A.![]() B.
B. ![]() C.
C.![]() D.
D.![]()
2.计算![]() 的结果是( )
的结果是( )
A.![]() B.
B.![]() C.
C.![]() D.以上答案都不对
D.以上答案都不对
3.若两圆的半径分别为4cm和6cm,两圆的圆心距为5cm,则两圆的位置关系是( )
 A.外离 B.外切
C.相交
D.内切
A.外离 B.外切
C.相交
D.内切
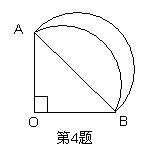
4.如图:扇形OAB中,![]() ,弦AB=
,弦AB=![]() ,
,
以AB为直径作半圆和![]() 围成图形面积为( )
围成图形面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.函数![]() 中自变量
中自变量![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.一次函数![]() 其中
其中![]() 不经过( )象限
不经过( )象限
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.若三点![]() 、
、![]() 、
、![]() 在反比例函数
在反比例函数![]() 的图象上,那么下面结论正确的是( )
的图象上,那么下面结论正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.在同一坐标系内,函数![]() 和
和![]() 的图象可能是( )
的图象可能是( )
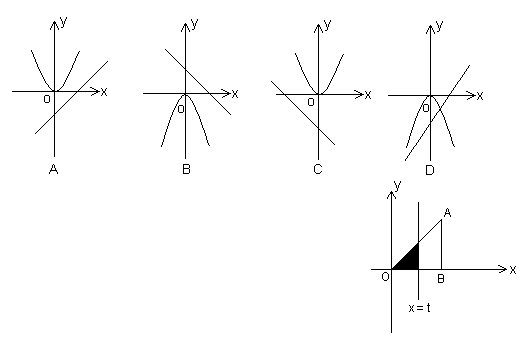 |
9.如右图,直角三角形AOB中,AB⊥OB于B,且
AB = OB =3,设直线![]() 截此三角形所得的阴影
截此三角形所得的阴影
部分的面积为S,则S与![]() 的函数关系的图象大致为( )
的函数关系的图象大致为( )
 |
10.在全国青年歌手大赛中,12名评委对其中一名歌手的打分如下:
8.70 8.80 8.80 8.60 8.85 9.00 8.90 8.75 8.90 8.95 8.80 8.85
这组数据中的中位数和众数以及去掉一个最高分和一个最低分后的平均分分别是( )
A.8.85 8.80 8.825 B.8.825 8.80 8.83
C.8.80 8.85 8.83 D.8.825 8.80 8.825
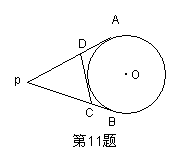 11.如图:PA、PB、CD都是⊙O的切线,∠P=600,设△PCD
11.如图:PA、PB、CD都是⊙O的切线,∠P=600,设△PCD
周长为C1,⊙O的周长为C2,则C2与2 C1的大小关系( )
A. ![]() B.
B.
![]()
C. ![]() D.
与⊙O的半径有关
D.
与⊙O的半径有关
第Ⅱ卷 (非选择题,共117分)
注意事项:
1. 本卷共八大题,请考生检查题数。
2. 本卷全部答案必须写在另页答题卷上,写在本卷上无效。
二、填空题:(每题3分,共21分)
12.梯形的上底长4cm,中位线长7cm, 则下底长 cm.
13.当![]() 时,方程
时,方程![]() 必有两个相等实数根.
必有两个相等实数根.
 14.某出租车公司在“国庆”长假平均每天的营业额为6万元,由此推断10月份的总
14.某出租车公司在“国庆”长假平均每天的营业额为6万元,由此推断10月份的总
营业额约为![]() (万元),根据所
(万元),根据所
学的统计知识,你认为这样的推断是否合理?
答: (答案选“合理”或“不合理”填写).
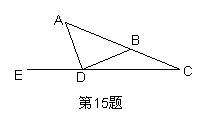
15.如图:已知AD=DB=BC,∠C=250,则∠ADE= 度.
16.函数![]() 的图象经过 象限.
的图象经过 象限.
17.已知两圆相内切,一个圆的半径是3,圆心距是2,那么另一个圆的半径是 .
18.已知半径为2的⊙A和半径为3的⊙B相外切,又⊙O的圆心在线段AB上,且⊙O与⊙A、⊙B都相交,则⊙O的半径![]() 的取值范围是 .
的取值范围是 .
三、(本题满分8分)
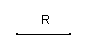
19.已知线段R,求作满足下列两个条件的图形:
(1)以R为半径的圆及把这个圆三等分的三点.
(2)在(1)的基础上作一个有且只有三条对称
轴的轴对称图形,并作出其对称轴.
(要写作法,并保留作图痕迹)
 |
四、(本题共2小题,每题9分,共18分)
20.解分式方程:![]()
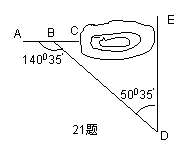
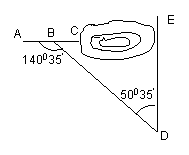
21.如图:某地区建设高速公路,在施工段上沿AC方向开山修路,为加快施工进度,要在山坡的另一边同时施工,如图所示,从AC上的一点B取∠ABD=![]() ,BD=380米,∠D=
,BD=380米,∠D=![]() ,那么开挖点E距离D多远,正好使A、C、E成一直线?(精确到0.1米)
,那么开挖点E距离D多远,正好使A、C、E成一直线?(精确到0.1米)
 |
五、(本题满分13分)
22、已知关于未知数x的方程![]() ,
,
(1)求使原方程有实数根的m的取值范围.
(2)试写出一个m值,使原方程两根中一个大于2,一个小于2,并解这个方程。
六、(本题满分13分)
23、如图:已知在同一平面内,△ABC是锐角三角形,M是△ABC外的一点,且∠AMC![]() ∠ABC,问是否至少还存在另一点
∠ABC,问是否至少还存在另一点![]() ,
,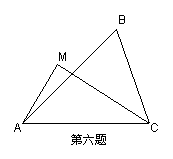 使
使![]() ,若不存在,请说明理由,若存在,请证明之.
,若不存在,请说明理由,若存在,请证明之.
七、(本题满分15分)
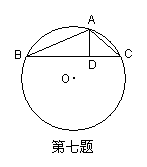
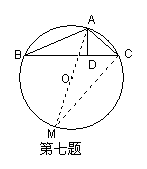
24、如图:在⊙O的内接△ABC中, AB+AC=12,
AD⊥BC于D,(点D不与点B、C重合),且AD=3,设⊙O的半径为![]() ,AB长是
,AB长是![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围。
的取值范围。
 |
八、(本题满分14分)
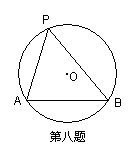 如图:已知AB是⊙O中一条长为4的弦,P是⊙O上一动点,
如图:已知AB是⊙O中一条长为4的弦,P是⊙O上一动点,![]() ,问:是否存在以A、P、B为顶点且面积最大的三角形,若不存在,请说明理由,若存在,请证明之,并求出此时三角形的最大面积。
,问:是否存在以A、P、B为顶点且面积最大的三角形,若不存在,请说明理由,若存在,请证明之,并求出此时三角形的最大面积。
九、(本题满分15分)
26、有一卖报人,从报社批进某种晚报的价格是每份1元,卖出的价格是每份1.5元,卖不掉的晚报,用每份0.4元的价格退回报社,在30天里有20天可卖出150份,其余10天只卖出100份,但是这30天每天从报社批进的份数必须相同,设每天批进的份数为x,每月的利润为y,请写出y与x的函数关系式,并求他应该每天从报社批进多少份时,才能使获得的月利润最高?月最高利润是多少元?
参考答案及评分标准
一、 选择题:(每题3分,共33分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 答案 | C | A | C | B | C | A | C | A | C | B | C |
二、 填空题:(每题3分,共21分)
12.10 13. ![]() 14.不合理 15. 75 16. 二、三、四
14.不合理 15. 75 16. 二、三、四
17. 1或5 (只填对1个给2分) 18. 0<r<5
 三、(本题满分8分)
三、(本题满分8分)
19.
(作出图形给3分)
作法:
1. 以R为半径作⊙O. 4分
2. 过圆心作直线l交⊙O于M、B
3. 以M为圆心,R的长为半径作弧,
交⊙O于A、C两点. 5分
4. 连AB、AC、BC 6分
5. 作直线AO、BO、CO 7分
则所得的图形为所求作的图形,三条对称轴分别为直线AO、BO、CO. 8分
(也可利用A、B、C三点作符合条件的其它图形,评分参考上述标准)
四、(本题共2小题,每题9分,共18分)
20.
解: 由原方程得:
![]() 2分
2分
整理得:![]() 4分
4分
![]() 5分
5分
![]()
![]() 7分
7分
 经检验:
经检验: ![]() 是增根
8分
是增根
8分
原方程的根是 ![]() 9分
9分
21.
解: 设AC的延长线交DE于E, 2分
则![]()
![]() 是Rt
是Rt![]() 4分
4分
![]() BD =
380米
BD =
380米
![]() 6分
6分
![]()
≈241.3(米) 8分
答:开挖点E距离D点241.3米时, 正好使A、C、E成一直线. 9分
五、(本题满分13分)
22.解:
(1)∵原方程有实数根
∴![]() 2分
2分
∴![]() 3分
3分
∴![]() 4分
4分
(2)取![]() ,
7分
,
7分
则
![]() 8分
8分
∴此时原方程为
![]() 11分
11分
![]()
![]() ,
,![]() 13分
13分
六、(本题满分13分)
23.解:在△ABC外至少还存在一点![]() ,使
,使![]() 2分
2分
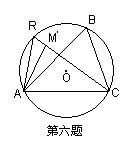 证明如下:
证明如下:
设⊙O是△ABC的外接圆,在弓形AMB内取异于
M的另一点![]() ,连
,连![]() 并延长交⊙O于R,
并延长交⊙O于R,
连AR 6分
则∠ARC=∠ABC. 8分
∵![]() 10分
10分
∴![]() 12分
12分
∴至少在△ABC外还存在另一点![]() ,使
,使![]() 13分
13分
 七.(本题满分15分)
七.(本题满分15分)
24.解: 连AO并延长交⊙O于M,连MC, 3分
则∠B=∠M, 4分
∵AM是直径
∴∠ACM=900 5分
又∵AD⊥BC
∴∠ACM =∠ADB 6分
∴△ABD∽△AMC 7分
∴![]() (1) 8分
(1) 8分
∵AB+AC=12,
∴AC=![]() 89分
89分
由(1)得:
![]() 10分
10分
整理得,![]() 11分
11分
∵![]() 12分
12分
∴![]() 13分
13分
解此不等式组得:![]() 14分
14分
即所求的函数关系式是:![]() 15分
15分
 八、(本题满分14分)
八、(本题满分14分)
25.解:存在以A、P、B为顶点且面积最大的三角形 1分
证明如下:
∵![]() 可知AB不是直径且P点一定在弦AB
可知AB不是直径且P点一定在弦AB
![]() 所对的优弧
所对的优弧![]() 上 2分
上 2分
![]() 过O作AB的垂线,交优弧
过O作AB的垂线,交优弧![]() 于
于![]() ,交AB于D,
,交AB于D,
![]() 此时
此时![]() 为优弧
为优弧![]() 上的点到AB的最大距离,
3分
上的点到AB的最大距离,
3分![]()
![]() 最大值等于
最大值等于![]() 4分
4分
连AO,则∠AOD=∠AP‘B, 5分
AD=DB=2 6分
![]()
![]() 7分
7分
![]() 8分
8分
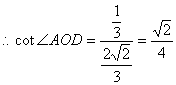 9分
9分
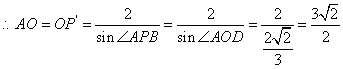 10分
10分
![]() 11分
11分
![]() 12分
12分
![]() 13分
13分
即![]() 14分
14分
九、(本题满分15分
26.解:设每天从报社批进![]() 份报纸,每月利润为
份报纸,每月利润为![]() 元, 1分
元, 1分
则
当![]() 时
时
![]() (1)
3分
(1)
3分
当![]() 时
时
![]()
![]() (2)
7分
(2)
7分
当![]() 时
时
![]()
=![]() (3) 11分
(3) 11分
∴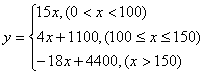 12分
12分
由(1) 、(2) 、(3)式可知,当![]() 时,
时,![]() 随
随![]() 的增大而增大, 13分
的增大而增大, 13分
∴当![]() 时,
时,
![]() 14分
14分
答:当每天批进150份报纸时,每月的利润最高,最高利润是1700元. 15分
(以上各解答题只提供其中一种解法的评分标准,若出现不同的解法可参照上述各题的解法评分标准给分)