2006年中考复习资料A卷最后一题
（一） 函数类
例一、荆州市2002年中考数学试题（本题满分12分）
如图，一次函数 
的图象与x轴、y轴交于点A、B，以线段AB为边在第一象限内作等边△ABC，
（1） 求△ABC的面积；
（2）
如果在第二象限内有一点P（a，
；试用含有a的代数式表示四边形ABPO的面积，并求出当△ABP的面积与△ABC的面积相等时a的值
（3） 在x轴上，是否存在点M，使△MAB为等腰三角形？若存在，请直接写出点M的坐标；若不存在，请说明理由。
例二、如图，有一座抛物线形拱桥，在正常水位时水面AB的宽为20m，如果水位上升3 m时，水面CD的宽是10 m．
（1）建立如图所示的直角坐标系，求此抛物线的解析式；
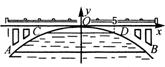（2）现有一辆载有救援物资的货车从甲地出发需经过此桥开往乙地，已知甲地距此桥280 km（桥长忽略不计）．货车正以每小时40 km的速度开往乙地，当行驶1小时时，忽然接到紧急通知：前方连降暴雨，造成水位以每小时0.25
m的速度持续上涨（货车接到通知时水位在CD处，当水位达到桥拱最高点O时，禁止车辆通行）．试问：如果货车按原来速度行驶，能否安全通过此桥?若能，请说明理由；若不能，要使货车安全通过此桥，速度应超过每小时多少千米?
例三、已知A（8，0）、B（0，6）、C（0，－2），连结AB，过点C的直线l与AB交于点P．
（1）如图①，当PB＝PC时，求点P的坐标；
（2）如图②，设直线l与x轴所夹的锐角为a，且
，连结AC，求直线l与x轴的交点E的坐标及△PAC的面积．
例四、北京市东城区2002年初中升学统一考试（本小题满分10分）
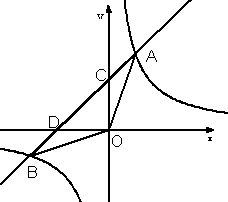已知：如图，一次函数的图象经过第一、二、三象限，且与反比例函数的图象交于A、B两点，与y轴交于点C，与x轴交于点D．OB＝
，tan∠DOB＝
．
（1）求反比例函数的解析式：
（2）设点A的横坐标为m，△ABO的面积为S，求S与m的函数关系式，并写出自变量m的取值范围；
（3）当△OCD的面积等于
时，试判断过A、B两点的抛物线在x轴上截得的线段长能否等于3．如果能，求此时抛物线的解析式；如果不能，请说明理由．
练习1、福建省福州市2002年初中毕业会考、高级中等学校招生考试（满分12分）
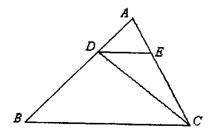
如图：已知△ABC中，AB＝4，D在AB边上移动（不与A、B重合），DE∥BC交AC与E，连结CD．设S△ABC＝S，S△DEC＝S1．
（1）当D为AB中点时，求S1∶S的值；
（2）若AD＝x，
，求y关于x的函数关系式及自变量x的取值范围；
（3）是否存在点D，使得S1＞
S成立？若存在，求出D点位置；若不存在，请说明理由．
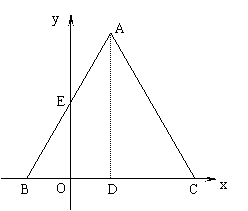练习2、已知△ABC是边长为4的等边三角形，BC在x轴上，点D为BC的中点，点A在第一象限内，AB与y轴的正半轴相交于点E，点B（-1，0），P是AC上的一个动点（P与点A、C不重合）
（1）（2分）求点A、E的坐标；
（2）（2分）若y=
过点A、E，求抛物线的解析式。
（3）（5分）连结PB、PD，设L为△PBD的周长，当L取最小值时，求点P的坐标及L的最小值，并判断此时点P是否在（2）中所求的抛物线上，请充分说明你的判断理由。