中考模拟试卷
初 三 数 学
(考试时间: 100分钟; 满分120分)
一、填空题(本大题共14题,每题3分,满分42分)
1.计算:-2 =____________.
2.分解因式:![]() =____________________.
=____________________.
3.如果关于![]() 的方程
的方程![]() 的一个根是 –1 , 那么
的一个根是 –1 , 那么![]()
4.不等式组![]() 的解集为___________.
的解集为___________.
5.已知![]() 是
是![]() 的反比例函数,它的图象经过点(-1,3),那么这个函数的解析式是____________.
的反比例函数,它的图象经过点(-1,3),那么这个函数的解析式是____________.
6.如果直线![]() 不经过第二象限,那么实数
不经过第二象限,那么实数![]() 的取值范围是______________.
的取值范围是______________.
7.方程![]() 的根是___________.
的根是___________.
8.函数![]() 自变量
自变量![]() 的取值范围是______________.
的取值范围是______________.
9. 点P(-1 , 2 )关于X轴的对称点P′的坐标是______________.
10.如果梯形一底边长为5,另一底边长为7,那么中位线长为_______________.
11.已两个相似三角形的面积之比是4:9,那么这两个三角形对应边的比是______________.
12.已知点G是△ABC的重心,GP//BC交AC边于点P,如果BC=12,那么GP=__________.
13.已知正方形ABCD的边长为1,如果将线段BD绕着点B旋转后,
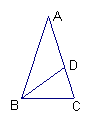 点D落在CB的延长线上D′处,连结D′A,
点D落在CB的延长线上D′处,连结D′A,
那么![]() 的值为_______________.
的值为_______________.
14. 如图,已知等腰△ABC中,顶角∠A=36°,
BD为∠ABC的平分线,那么![]() 的值为_______________.
的值为_______________.
二、选择题(本大题共4题,每题3分,满分12分)
【下列每题列出的四个答案中,只有一个是正确的,把正确答案的代号填入括号内】
15.下列运算中,计算结果正确的是………………………………………( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
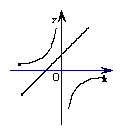
 16.如图,函数
16.如图,函数![]() 与
与![]() 在同一直角坐标系内的图象仅可能是…( )
在同一直角坐标系内的图象仅可能是…( )
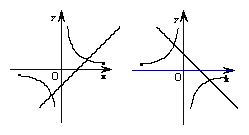 |
(A) (B) (C) (D)
17.下列命题中错误的是……………………………………………………( )
(A)平行四边形的对角相等 (B)两条对角线相等的平行四边形是矩形
(C)等腰梯形的对角线相等 (D)对角线互相垂直的四边形是菱形
18.如果两圆的半径分别为3、5,圆心距为2,那么两圆的位置关系为…( )
(A)外切 (B)相交 (C)内切 (D)内含
三、(本大题共3题,每题8分,满分24分)
19.解方程组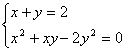
20.如图,在直角梯形ABCD中,AD//BC, DC⊥BC,E为BC边上的点,将直角梯形ABCD沿对角线BD折叠,使△ABD△与EBD重合.若∠A=120°,AB=4![]() ,求EC的长.
,求EC的长.
 |
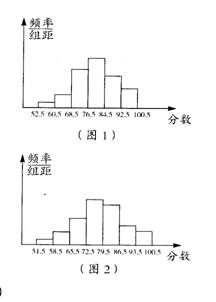 21.在一次环保知识测试中,初三(1)班的两名学生根据班级成绩(分数为整数)分别绘制了组距不同的频率分布直方图,如图1、图2 .已知,图1从左到右每个小组的频率分别为:0.04、0.08、0.24、0.32、0.20、0.12,其中68.5~76.5小组的频数为12;图2从左到右每个小组的频数之比为1:2:4:7:6:3:2,请结合条件和频率分布直方图回答下列问题:
21.在一次环保知识测试中,初三(1)班的两名学生根据班级成绩(分数为整数)分别绘制了组距不同的频率分布直方图,如图1、图2 .已知,图1从左到右每个小组的频率分别为:0.04、0.08、0.24、0.32、0.20、0.12,其中68.5~76.5小组的频数为12;图2从左到右每个小组的频数之比为1:2:4:7:6:3:2,请结合条件和频率分布直方图回答下列问题:
(1) 初三(1)班参加测试的人数为________人;
(2)若这次测试成绩80分以上(含80分)为优秀,
则优秀人数为_______人,优秀率为__________;
(3)若这次测试成绩60分以上(含60分)为及格,
则及格率为__________.
四、(本大题共3题,每题10分,满分30分)
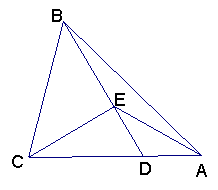 22. 如图,△ABC中D为AC上一点,CD=2DA,∠BAC=45°,∠BDC=60°,CE⊥BD,E为垂足,连结AE.
22. 如图,△ABC中D为AC上一点,CD=2DA,∠BAC=45°,∠BDC=60°,CE⊥BD,E为垂足,连结AE.
求证:(1) ED=DA;
(2)∠EBA=∠EAB
(3) BE2=AD·AC
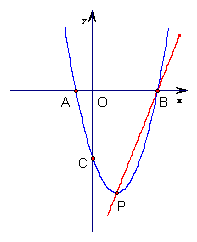 23.如图,在平面直角坐标系内,O为坐标原点,点A在
23.如图,在平面直角坐标系内,O为坐标原点,点A在![]() 轴负半轴上,点B在
轴负半轴上,点B在![]() 轴正半轴上,且OB > OA . 设点C (0 , -4 ),
轴正半轴上,且OB > OA . 设点C (0 , -4 ), ![]() ,线段OA、OB的长是关于
,线段OA、OB的长是关于![]() 的一元二次方程
的一元二次方程![]() 的两个根.
的两个根.
(1) 求过A、B、C三点的抛物线的解析式;
(2) 设上述抛物线的顶点为P,求直线PB的解析式.
.
24.陈海公路上一路段的道路维修工作准备对外招标,现有甲、乙两个工程队竞标,竞标资料上显示:若由两队合做,6天可以完成,共需工程费用7800元;若单独完成此项工程,甲队比乙队少用5天,但甲队每天的工程费比乙队多300元。工程指挥部决定从这两个队中选一个队单独完成此项工程,若从节省资金的角度考虑,应该选择哪个工程队?为什么?
五、(本题满分12分)
25.如图,直角坐标系内的矩形ABCD中顶点A的坐标为(0,3),BC=2AB,P为AD边上一动点(与点A、D不重合),以点P为圆心作⊙P,与对角线AC相切于点F,过P、F作直线![]() ,交BC边上于点E .当点P运动到点
,交BC边上于点E .当点P运动到点![]() 位置时,直线
位置时,直线![]() 恰好经过点B,此时直线的解析式是
恰好经过点B,此时直线的解析式是![]() .
.
(1) 求BC、AP1的长;
(2)
设AP=![]() ,梯形PECD的面积为S,求S关于
,梯形PECD的面积为S,求S关于![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
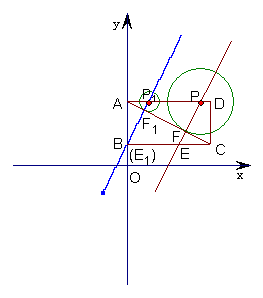 (3)以点E为圆心作⊙E,与
(3)以点E为圆心作⊙E,与![]() 轴相切 .试探究并猜想⊙P和⊙E有哪几种不同的位置关系,并求出AP相应的取值范围.
轴相切 .试探究并猜想⊙P和⊙E有哪几种不同的位置关系,并求出AP相应的取值范围.
中考模拟试卷
参考答案及评分标准 2005.4
一、1. 2 ;
2. ![]() ; 3. 2 ; 4.
; 3. 2 ; 4. ![]() ; 5.
; 5. ![]()
6. m≤0 ; 7. 2 ; 8. ![]() ; 9. ( -1 , -2 ) ; 10. 6 ; 11. 2 ∶3
; 9. ( -1 , -2 ) ; 10. 6 ; 11. 2 ∶3
12. 4 ; 13. ![]() ; 14.
; 14. ![]()
二、15. B 16. C 17. D 18. C
三、
19.解:原方程组可变形为(Ⅰ)![]() ……(2分) 或(Ⅱ)
……(2分) 或(Ⅱ) ![]() ……(2分)
……(2分)
由(Ⅰ)得 ![]() ……(2分)
由(Ⅱ)得
……(2分)
由(Ⅱ)得![]() ……(2分)
……(2分)
∴原方程组的解为![]() 或
或 ![]()
20.解: ∵△ABD与△EBD关于对角线BD对称
∴∠BED=∠A=120°……………………………………(1分)
∵点E在BC边上 ∴∠DEC=60°…………………(1分)
∵AD∥BC ∴∠ABC=60°…………………………(1分)
∴∠ABC=∠DEC ∴AB∥DE………………………(1分)
∴四边形ABCD为平行四边形………………………(1分)
∴DE=AB=4……………………………………………(1分)
在Rt△DEC中, ![]() …………………(1分)
…………………(1分)
∴EC=![]() ×4=2………………………………………(1分)
×4=2………………………………………(1分)
21. (1) 50 (2) 22 ; 44% (3) 96% (每空格2分)
22.证明:(1) ∵CE⊥BD ∴∠CED=90° 又 ∠BDC=60°∴∠ECD=30°……(1分)
∴CD=2ED …………………………(1分)
∵CD=2DA ∴ED=DA…………………………(1分)
(2) ∵ED=DA ∴∠DEA=∠DAE
∵∠EDC=60° ∴∠EAD=∠DEA=30°………………………(1分)
∵∠BAD=45° ∴∠EAB=15°…………………………………(1分)
又∠BDC=∠DBA+∠BAD ∴∠DBA=15°
∴∠EAB=∠EBA……………………………(1分)
(3) ∵∠EAB=∠EBA ∴BE=AE……………………………………(1分)
∵∠AED=∠ACE ∴△AED∽△ACE…………………………(1分)
∴![]() ………………………(1分)
………………………(1分)
∴AE2=AD·AC 即BE2=AD·AC………………………(1分)
23.解(1) ∵OA、OB是方程x2-mx+2(m-3)=0的两个根.
∴OA+OB= m OA·OB=2(m-3)………………(1分)
∵OA2+OB2=17 ∴(OA+OB)2-2OA·OB=17
∴m2-4(m-3)=17 ∴m2-4m-5=0……………(1分)
∴m1=5, m2=-1………………………………(1分)
∵OA+OB= m > 0 ∴m = -1 (舍去) ………………(1分)
当m=5时, x2-5x+4=0 ∴x1=1. x2=4………(1分)
∵OB>OA ∴PA=1, OB=4 按题意得 A(-1, 0), B(4, 0)………(1分)
设所求抛物线的解析式为![]()
则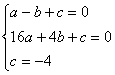 解得
解得 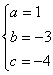
∴ 抛物线的解析式为![]() …………………(1分)
…………………(1分)
(2)∵![]() ∴点
∴点![]() ………(1分)
………(1分)
设直线PB的解析式为![]() ………………………(1分)
………………………(1分)
则 解得
解得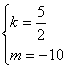 即
即![]() …………(1分)
…………(1分)
24.解:设甲工程队单独完成需x天,每天需费用m元,
则乙工程队单独完成需(x+5)天,每天需费用 (m-300)元.……(1分)
根据题意,得 ![]() ……………………………………(3分)
……………………………………(3分)
∴x2-7x-30=0……………………………………(1分)
∴x1=10, x2=-3
经检验,x1=10,x2=-3 都是原方程的解. 但x2=-3不合题意, 舍去.
∴x=10…………………………………………(1分)
又6(m+m-300)=7800 解得 m=800…………(1分)
∴甲工程队单独完成需费用10×800=8000(元),……(1分)
则乙工程队单独完成需费用15×500=7500(元).……(1分)
答:若由一个队单独完成此项工程,从节约资金的角度考虑,
应由乙工程队单独完成.……………………………(1分)
25.解(1)由y=2x+1可知, 当x=0时 ,y=1 ∴ 点B(0,1) ………(1分)
∵点A(0,3) ∴AB=2 又 BC=2AB ∴ BC=4………(1分)
∵点P1在直线y=2x+1和AD边上,又AD // X轴
, ∴可设![]() )
)
则 ![]() 即
即![]() ∴
∴![]() ………………(1分)
………………(1分)
∴AP1=1………………………………(1分)
(2) ∵AP=m AD=4 AP1=1 ∴PD = 4-m P1P = m-1……………(1分)
又P1P//BE,P1B//PE, ∴P1PEB是平行四边形.
∴BE=P1P ∴EC = 4-(m-1) = 5-m……………(1分)
∴S=![]() [(4-m)+(5-m)]×2 = 9-2m……………(1分)
[(4-m)+(5-m)]×2 = 9-2m……………(1分)
1≤m<4………………………………………(1分)
(3) 当⊙E与![]() 轴及⊙P外切时,EF=1, ∵ △CFE∽△CBA
轴及⊙P外切时,EF=1, ∵ △CFE∽△CBA
∴![]() ∴
∴![]() 即EC=
即EC=![]() ……………(1分)
……………(1分)
∴BE=4-![]() 即m-1=4-
即m-1=4-![]() ∴m=5-
∴m=5-![]()
∴当m=5-![]() 时, ⊙P与⊙E外切……………(1分)
时, ⊙P与⊙E外切……………(1分)
当1≤m<5-![]() 时, ⊙P与⊙E外离……………(1分)
时, ⊙P与⊙E外离……………(1分)
当5-![]() <m<4时, ⊙P与⊙E相交……………(1分)
<m<4时, ⊙P与⊙E相交……………(1分)