1、
 |
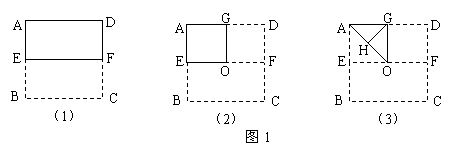一张正方形纸片ABCD第一次对折，使BC和AD重合，得到折痕EF如图（1），第二次对折，使DF与AE重合如图（2），第三次对折，沿对角线AO对折，使E与G，此时用剪刀沿GH剪掉三角形AGH及其下面的折叠部分，使OH=OG，然后展开，问得到一个什么图形？在这张正方形纸片上得到这样的图形是否最大？
2、
 |
三等分角仪——把材料制成图2的中阴影部分的的形状，使AB与半圆的半径CB、CD相等，PB垂直于AD。这便做成了“三等分角仪”。如果要把∠MPN三等分时，可将三等分角仪放在∠MPN上，适当调整它的位置，使PB通过角的顶点P，使A点落在角的PM边上，使角的另一边与半圆相切于E点，最后通过B、C两点分别作两条射线PB、PC，则∠MPB=∠BPC=∠CPN。请说明理由。
3、 如图3，一个等边三角形的边长与和它的一边相切的圆的周长相等，当这个圆按箭头方向从某一位置沿等边三角形的三边做无滑动旋转，直至回到原出发位置时，问该圆转了几圈？
4、
 |
如图4甲，根据四边形不稳定性制作的边长为16cm的可活动的菱形衣架。如图乙，若墙上钉子间的距离AB=BC=16cm，则∠1=_____
5、 请你把一张矩形纸片折成正方形、平行四边形、菱形。
6、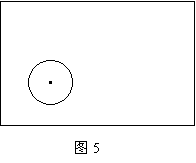 
请你设计一种方案求出15°的三角函数值。
7、 图5是由圆和矩形组成的一个图形，请你用一条直线把它们分成周长和面积都相等的两部分。
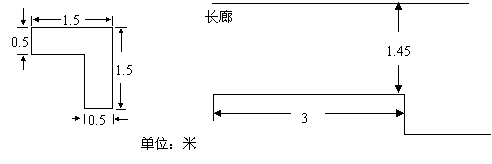
8、如图所示是某立式家具（角书橱）的横断面，请你设计一个方案（角书橱高2米，房间高2.6米，所以不必从高度方面考虑方案的设计），按此方案，可使该家具通过图乙中的长廊搬入房间。在图乙中把你设计的方案画成草图，并说明按此方案可把家具搬入房间的理由（注：搬运过程中不准拆卸家具，不准损坏墙壁）
 |
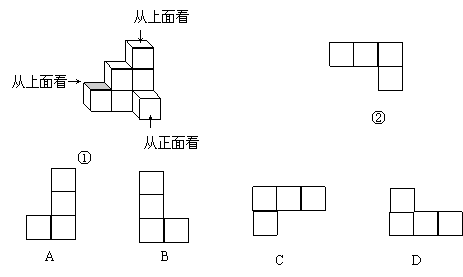9、我们从不同的方向观察同一物体时，可能看到不同的图形。如图，图①是由若干个小正方体所搭成的几何体，图②是从图①的上面看这个几何体所看到的图形，那么从图①的左面看这个几何体所看到的图形是（ ）
10、福州市实施容貌工程期间某学校楼前铺设小广场地面。其图案设计如图，正方形小广场地面的边长是40m，中心建一直径为20m的圆形花坛，四角各留一个边长为10m的小正方形花坛。种植高大树木，图中阴影处铺设广场砖。
（1） 计算阴影部分的面积S（л取3）；
（2） 某施工队承包广场砖的任务，计划在一定时间内完成。按计划工作一天后，改进了工艺，每天比原计划多铺60m2，结果提前3天完成了任务。原计划每天铺多少平方米？
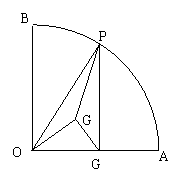11、如图，在半径为6、圆心角为90°的扇形OAB的AB上，有一个动点P，PH⊥OA，垂足为H，G为△OPH三条中线的交点。
（1） 当点P在AB上运动时，线段GO、GO、GH中，有无长度保持不变的线段？如果有，请指出这样的线段，并求出相应的长度；
（2） 设PH=x，GP=y，求y关于x的函数解析式，并写出函数的定义域；
（3） 如果△PGH是等腰三角形，试求出线段PH的长。
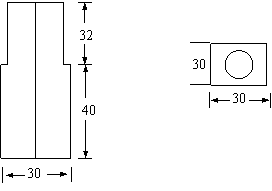12、如图是一个几何体的二视图，求该几何体的体积（л取3.14）。单位：cm