深圳市罗湖区2005年初中毕业学业考试
数学模拟试卷
命题: 文锦中学 张建平
说明:全卷共七大题,共8页,考试时间90分钟,满分100分。
一、选择题(本题有10小题,每题3分,共30分).每小题给出4个答案,其中只有一个是正确的.请把正确答案的字母代号填写在括号里.
1、检查5个篮球的质量,把超过标准质量的克数记为正数,不足标准质量的克数记为负数,检查结果如下表:
| 篮球编号 | 1 | 2 | 3 | 4 | 5 |
| 与标准质量的差(克) | +4 | +7 | -3 | -8 | +9 |
质量最大的篮球比质量最小的篮球重( )
A、12克 B、15克 C、17克 D、19克

2、如图,A、B、C、D是⊙O上的三点,∠BAC=30°,
则∠BOC的大小是 ( )
A、60° B、45° C、30° D、15°
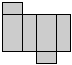
3、下面的4幅图中,经过折叠不能围成一个立体图的一幅是 ( )
 | |||||||
 | |||||||
 | |||||||
 | |||||||
A B C D
4、某中学新科技馆铺设地面,已有正三角形形状地砖.现打算购买另一种不同形状的正多边形地砖,与正三角形地砖在同一顶点处平面镶嵌,则该学校不应该购买的地砖形状是( )
A. 正方形 B.正六边形 C.正八边形 D.正十二边形
5、已知正比例函数![]() 的图象上两点
的图象上两点![]() 、
、![]() ,当
,当![]() 时,有
时,有![]() ,那么m的取值范围是( ).
,那么m的取值范围是( ).
A. ![]() B.
B. ![]() C.
C.![]() D.
D. ![]()
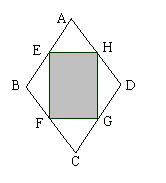 6、小明爸爸的风筝厂准备购进甲、乙两种规格相同但颜色不同的布料生产一批形状如图5所示的风筝,点E,F,G,H分别是菱形ABCD各边的中点。其中阴影部分用甲布料,其余部分用乙布料(裁剪两种布料时,均不计余料)。若生产这批风筝需要甲布料20匹,那么需要乙布料
6、小明爸爸的风筝厂准备购进甲、乙两种规格相同但颜色不同的布料生产一批形状如图5所示的风筝,点E,F,G,H分别是菱形ABCD各边的中点。其中阴影部分用甲布料,其余部分用乙布料(裁剪两种布料时,均不计余料)。若生产这批风筝需要甲布料20匹,那么需要乙布料
A.10匹 B.15匹
C.20匹 D.40匹
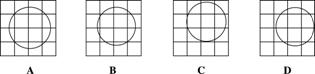
7、下列每张方格纸上都画有一个圆,只用不带刻度的直尺就能确定圆心位置的是( )
8.下面的扑克牌中,牌面是中心对称图形的是( )
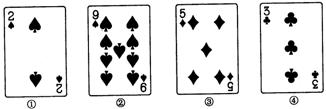
A、①② B、③④ C、②④ D、①③
9、已知抛物线![]() 的部分图象(如图7),图象再次与x轴相交时
的部分图象(如图7),图象再次与x轴相交时
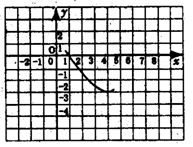 的坐标是( )
的坐标是( )
A.(5,0) B.(6,0)
C.(7,0) D.(8,0)
10、某次“迎奥运”知识竞赛中共有20道题,对于每一道题,答对了10分,答错了或不答扣5分,至少要答对( )道题,其得分才会不少于95分?
A.14 B.13 C.12 D.11
二、填空题(本题有5小题,每题3分,共15分.请把答案填在相应的题号下.)
![]()
![]()
![]()
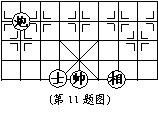 11、如图,如果 所在位置的坐标为(
11、如图,如果 所在位置的坐标为(![]() ,
,![]() ), 所
), 所
在位置的坐标为(![]() ,
,![]() ), 那么, 所在位置的坐
), 那么, 所在位置的坐
标为 ;
12、下图是2004年6月份的日历,如图中那样,用一个圈竖着圈住3个数.如果被圈的三个数的和为36,则这三个数中最大的一个为 .
| 日 | 一 | 二 | 三 | 四 | 五 | 六 |
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 |
| 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 |
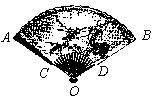 |
13、如图,一扇形纸扇完全打开后,两竹条外侧OA和OB的夹角为120°,OC长为8cm,贴纸部分的CA长为15cm,则贴纸部分的面积为 cm2(结果保留π)
14、某体育馆用大小相同的长方形木块镶嵌地面,第1次铺2块,如图1;第2次把第1次铺的完全围起来,如图2;第3次把第2次铺的完全围起来,如图3;…。依此方法,第10次铺完后,第10次镶嵌使用的木块数是____________
![]()

![]()
![]()
![]()
图1 图2 图3
15、“黑洞”是个非常奇怪的天体,它体积小,密度大,吸引力强,任何物体到了它那里都别想再“爬”出来。无独有偶,数字中也有类似的“黑洞”,满足某种条件的所有数,通过一种运算,都能被它“吸”进去,无一能逃脱它的魔掌。譬如:任意找一个3的倍数的数,先把这个数的每一个数位上的数字都立方,再相加,得到一个新数,然后把这个新数的每一个数位上的数字再立方、求和,…,重复运算下去,就能得到一个固定的数T= ,我们称它为数字“黑洞”
三、解答题(本部分共27分,第16、17题各4分,第18、19、21题各6分,第20题7分)
16.(4分)先化简代数式,再求值:![]() 其中x=2
其中x=2
解:
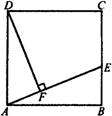
17、如图,![]() 是正方形,点
是正方形,点![]() 在
在![]() 上,
上,![]() 于
于![]() ,请你在
,请你在![]() 上确定一点
上确定一点![]() ,使
,使![]() ,并说明理由。
,并说明理由。
 |
18、先阅读下列一段文字,然后解答问题。
某运输部门规定:办理托运,当一件物品的重量不超过a千克(a<18)时,需付基础费30元和保险费b元;为限制过重物品的托运,当一件物品的重量超过a千克时,除了付以上基础费和保险费外,超过部分每千克还需付c元超重费。
设某件物品的重量为x千克,支付费用为y元。
(1)当0<x≤a时,y=_________(用含b的代数式表示);
当x>a时,y=________(用含x和a,b,c的代数式表示)。
(2)甲、乙、丙三人各托运了一件物品,物品重量与支付费用如下表所示:
| 物品重量(千克) | 支付费用(元) |
| 12 | 33 |
| 18 | 39 |
| 25 | 60 |
①试根据以上提供的信息确定a、b、c的值,并写出支付费用y(元)与每件物品重量x(千克)的函数关系式。
②试问在物品可拆分的情况下,用不超过120元的费用能否托运50千克物品?若能,请设计出其中一种托运方案,并求出托运费用;若不能,请说明理由。
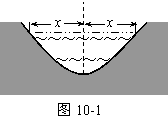 19、如图10-1是某段河床横断面的示意图。查阅该河段的水文资料,得到下表中的数据:
19、如图10-1是某段河床横断面的示意图。查阅该河段的水文资料,得到下表中的数据:
| x(米) | 5 | 10 | 20 | 30 | 40 | 50 |
y(米) | 0.125 | 0.5 | 2 | 4.5 | 8 | 12.5 |
(1)请你以上表中的各对数据(x,y)作为点的坐标,尝试在图10-2所示的坐标系中画出y关于x的函数图像;
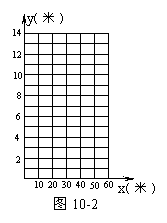
(2) ①填写下表:
x | 5 | 10 | 20 | 30 | 40 | 50 |
|
|
②根据所填表中数据呈现的规律,猜想出用 x表示y的二次函数表达式:
(3)当水面宽度为36米时,一艘吃水深度(船底部到水面的距离)为1.8米的货船能否在这个河段安全通过?为什么?
20、在本学期某次考试中,某校初三⑴、初三⑵两班学生数学成绩统计如下表:
| 分数 | 50 | 60 | 70 | 80 | 90 | 100 | |
| 人数 | 三⑴班 | 3 | 5 | 16 | 3 | 11 | 12 |
| 三⑵班 | 2 | 5 | 11 | 12 | 13 | 7 | |
请根据表格提供的信息回答下列问题:
⑴ 三⑴班平均成绩为_________分,三⑵班平均成绩为________分,从平均成绩看两个班成绩谁优谁次?
⑵ 三⑴班众数为________分,三⑵班众数为________分。从众数看两个班的成绩谁优谁次?____________________。
⑶已知三⑴班的方差大于三⑵班的方差,那么说明什么?
21、集市上有一个人在设摊“摸彩”,只见他手拿一个黑色的袋子,内装大小、形状、质量完全相同的白球20只,且每一个球上都写有号码(1-20号)和1只红球,规定:每次只摸一只球。摸前交1元钱且在1——20内写一个号码,摸到红球奖5元,摸到号码数与你写的号码相同奖10元。
(1) 你认为该游戏对“摸彩”者有利吗?说明你的理由。
(2) 若一个“摸彩”者多次摸奖后,他平均每次将获利或损失多少元?
四、实践与操作题(4分)
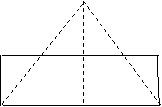
22、正方形通过剪切可以拼成三角形。方法如下:
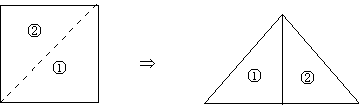
图(1)
仿上面图示的方法,解答下列问题:(画图、标示)
(1)如图(2),对直角三角形,设计一种方案,将它分成若干块,再拼成一个与原三角形等面积的矩形。
(2)如图(3)对于任意三角形,设计一种方案,将它分成若干块,再拼成一个原三角形等面积的矩形。

图(2) 图(3)
五、应用题(本题6分)
23、甲、乙两件服装的成本共500元,商店老板为获取利润,决定将甲服装按50%的利润定价,乙服装按40%的利润定价。在实际出售时,应顾客要求,两件服装均按9折出售,这样商店共获利157元,求甲、乙两件服装的成本各是多少元?
解:
六、图表阅读分析题(本题8分)
24、国家课改某实验区在2004年进行了中考评价改革:由过去的“分分计较”变为注重对学生“学业水平”的考核,下面列举了部分考试科目的相关信息。
| 语文 | 数学 | 英语 | 物理 | 化学 | |
| 2004年中考试卷满分 | 100分 | 100分 | 100分 | 100分 | 100分 |
| 方法:2004年采用将考生各科的中考分数转化“等级(A、B、C、D、E、F)” ,再计算各科等级的位次值之和作为毕业和高一级学校录取的重要依据 | 90分≤X≤100分, 记为A等级,位次值为6 80分≤X≤89分, 记为B等级,位次值为5 70分≤X≤79分, 记为C等级,位次值为4 60分≤X≤69分, 记为D等级,位次值为3 40分≤X≤59分, 记为E等级,位次值为2 0分≤X≤39分, 记为F等级,位次值为1 规则:X(X为整数)为考生各科的中考分数,当两人各科的位次值之和相同时,则采用“金牌领先原则”:即谁的A等级的个数多,则谁的名次排在前;若A等级一样,则看B等级个数,依次类推… | ||||
问题1:刘小明同学的五科等级为1A4B,张小思同学的五科等级为2A2B1C,马小虎同学的五科等级为1A3B1C,请分别计算三人的位次值之和,并将三人的成绩按规则由优到劣依次进行排序。
问题2:孙大力同学参加中考,五科位次值之和为25(已知他五科等级中均没有D、E、F这三个等级),试问他五科中有几个A,几个B,几个C?
七、综合探究题(本题10分)
25、 如图,有一块塑料矩形模板ABCD,长为10cm,宽为4cm,将你手中足够大的直角三角板 PHF 的直角顶点P落在AD边上(不与A、D重合),在AD上适当移动三角板顶点P:
①能否使你的三角板两直角边分别通过点B与点C?若能,请你求出这时 AP 的长;若不能,请说明理由.(5分)
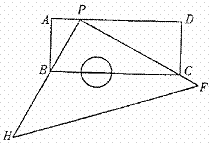 ②再次移动三角板位置,使三角板顶点P在AD上移动,直角边PH 始终通过点B,另一直角边PF与DC的延长线交于点Q,与BC交于点E,能否使CE=2cm?若能,请你求出这时AP的长;若不能,请你说明理由.(5分)
②再次移动三角板位置,使三角板顶点P在AD上移动,直角边PH 始终通过点B,另一直角边PF与DC的延长线交于点Q,与BC交于点E,能否使CE=2cm?若能,请你求出这时AP的长;若不能,请你说明理由.(5分)
![]() 深圳市罗湖区2005年初中毕业学业考试
深圳市罗湖区2005年初中毕业学业考试
数学模拟试卷参考答案
命题: 文锦中学 张建平
一、选择题:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | C | A | D | C | A | C | A | D | C | B |
二、填空题:
11.(-3,1) 12. 19 13. 310π 14. 74 15. 153
三、
16. 原式=![]()
把x=2代入:
原式=![]()
17.过B作BG⊥AE于G
证明:(略)
18.(1)30+b 30+b+c(x-a)
(2 ) ①解:将上表中的数据代入得
![]()
![]() 30+b=33
a= 16
30+b=33
a= 16
30+b+c(18-a)=39 解得 b=3
30+b+c(25-a)=60 c=3
支付费用y(元)与每件物品重量x(千克)的函数关系式为:y=3x-15
② 能。
设计方案:将50千克的物品拆分成两个25千克托运
这样所付费用为60+60=120元
19. (1) 略
(2)①
| x | 5 | 10 | 20 | 30 | 40 | 50 |
|
| 200 | 200 | 200 | 200 | 200 | 200 |
② ![]()
③当x=18时,y=1.62<1.8,所以不能安全通过
20.(1)80,80,两班一样
(2)70,90,三(2)班更优秀
(3)三(1)班的成绩差异较大,三(2)班的成绩较均衡。
21.(1)对“摸彩”者不利,因为获奖概率较小。
(2)![]() ,所以平均每次将损失
,所以平均每次将损失![]() 元。
元。
 四、22.(1)
(2)
四、22.(1)
(2)
五、23.设:甲服装的成本为x元,则:乙服装的成本为(500-x)元
根据题意,可列方程:
(1+50%)x·90%+(1+40%)(500-x)·90%=157+500
解得: x=300
500-300=200(元)
答:甲、乙两件服装的成本分别是300元、200元。
六、24.(1)刘小明:1×6+4×5=26;
张小思:2×6+2×5+1×4=26;
马小虎:1×6+3×5+1×4=25
排序:张小思 刘小明 马小虎
(2) 设:五科中有x个A,y个B,z个C
根据题意,可列方程:组
![]() x+y+z=5
x+y+z=5
6x+5y+z=25
由于x,y,z是非负整数,所以可得解:
![]()
![]()
![]() x1=2 x2=1 x3=0
x1=2 x2=1 x3=0
y1=1 y2=3 y3=5
z1=2 z2=1 z3=0
答:五科中有2个A,1个B,2个C或1个A,3个B,1个C或5个B。
七、(1)能。
AP=2cm或8cm
(2)能。
AP=4cm