2005年襄樊市初中升学统一考试
数学试题
卷Ⅰ 选择题(36分)
一、选择题(本大题共12道小题,每小题3分,共36分,在每小题给出的四个选项中,只
有一项是符合题目要求的,请将其序号在答题卡中涂黑作答.)
1.某地一天早晨的气温是![]() ℃,中午上升了11℃,午夜又下降了9℃,则午夜的气温是
℃,中午上升了11℃,午夜又下降了9℃,则午夜的气温是
A.5℃ B.![]() ℃ C.
℃ C.![]() ℃ D.
℃ D.![]() ℃
℃
2.下列计算错误的是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.实数![]() 在数轴上表示如图1所示,则下列结论错误的是
在数轴上表示如图1所示,则下列结论错误的是
图1
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.某商场对一种家电商品作调价,按原价的8折出售,仍可获利10%,此商品的原价是2200元,则商品的进价是
A.1540元 B.1600元 C.1690元 D.1760元
5.下列说法正确的是
A.若![]() ,则
,则![]() B.
B.![]() ,则
,则![]()
C.![]() D.5的平方根是
D.5的平方根是![]()
6.若方程组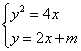 有一个实数解,则
有一个实数解,则![]() 的值是
的值是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.在匀速运动中,路程![]() (千米)一定时,速度
(千米)一定时,速度![]() (千米/时)关于时间
(千米/时)关于时间![]() (小时)的函数图象大致是
(小时)的函数图象大致是
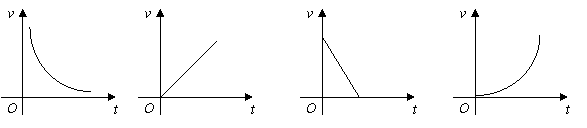 |
A B C D
图2
8.下列四个生活、生产现象:①用两个钉子就可以把木条固定在墙上;②植树时,只要定出两棵树的位置,就能确定同一行树所在的直线;③从![]() 地到
地到![]() 地架设电线,总是尽可能沿着线段
地架设电线,总是尽可能沿着线段![]() 架设;④把弯曲的公路改直,就能缩短路程,其中可用公理“两点之间,线段最短”来解释的现象有
架设;④把弯曲的公路改直,就能缩短路程,其中可用公理“两点之间,线段最短”来解释的现象有
A.①② B.①③ C.②④ D.③④
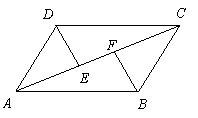 9.如图3,
9.如图3,![]() 是
是![]() 对角线
对角线![]() 上两点,且
上两点,且![]() ,连结
,连结![]() 、
、![]() ,则图中共有全等三角形的对数是
,则图中共有全等三角形的对数是
|
A.1对 B.2对 C.3对 D.4对
10.![]() 的半径为5cm,弦
的半径为5cm,弦![]() ,
,![]() ,则
,则![]() 和
和![]() 的距离是
的距离是
A.7cm B.8cm C.7cm或1cm D.1cm
11.一块半径为30cm,圆心角为![]() 的扇形铁皮,做成一个圆锥的侧面(粘合部分忽略不计),则该圆锥的底面半径是
的扇形铁皮,做成一个圆锥的侧面(粘合部分忽略不计),则该圆锥的底面半径是
A.30cm B.20cm C.10cm D.15cm
12.甲、乙两人各打靶5次,已知甲所中的环数是8,7,9,7,9,乙所中的环数的平均数是![]() ,方差
,方差![]() ,那么对甲、乙射击成绩正确判断是
,那么对甲、乙射击成绩正确判断是
A.乙的射击成绩较稳定 B.甲的射击成绩较稳定
C.甲、乙的射击成绩稳定性相同 D.甲、乙的射击成绩无法比较
卷Ⅱ 非选择题(84分)
二、填空题(本大题共6道小题,每小题3分,共18分,把答案填在题中横线上)
13.分解因式:![]() .
.
14.若一次函数![]() 的图象不过第一象限,则
的图象不过第一象限,则![]() 的取值范围是 .
的取值范围是 .
15.同一时刻,高为1.5m标杆影长为2.5m,一古塔在地面的影长为50m,那么古塔的高为
m.
16.已知实数![]() 满足等式
满足等式![]() ,
,![]() ,则
,则![]() 的值是 .
的值是 .
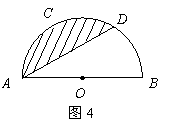 17.如图4,已知半圆的直径
17.如图4,已知半圆的直径![]() 4cm,点
4cm,点![]() 是这个
是这个
半圆的三等分点,则弦![]() 和
和![]() 围成的阴影部分面
围成的阴影部分面
积为 cm2.
18.如图5,用有花纹和没有花纹的两种正方形地面砖按图5中所示的规律拼成若干图案,则第![]() 个图案中没有花纹的地面砖有 块.
个图案中没有花纹的地面砖有 块.
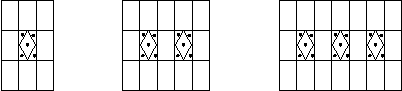 |
第一个图案 第二个图案 第三个图案
三、解答题(本大题共8道小题,共计66分,解答应写出文字说明、证明过程或演算步骤)
19.(本题满分6分)
先化简,在求值
![]() .其中
.其中![]()
20.(本题满分6分)
今年,某县(市)有14000名考生参加了理化生实验操作考试,现随机抽查100名考生的考试成绩(满分100分,分数取整数),列出频率分布表如下:
(1) 补全频率分布表;
(2) 若规定考试成绩不低于80分的为优秀,则这次考试的优秀率是多少?该县(市)理
化实验操作考试成绩为优秀的约有多少名?
| 分组 | 频数 | 频率 |
| 39.5~49.5 | 6 | 0.06 |
| 49.5~59.5 | 10 | 0.10 |
| 59.5~69.5 | 22 | |
| 69.5~79.5 | 0.20 | |
| 79.5~89.5 | ||
| 89.5~100.5 | 16 | 0.16 |
| 合计 | 100 | 1.00 |
21.(本题满分6分)
解方程![]()
22.(本题满分7分)
我们在探索平面图形性质时,往往通过剪拼的方式帮助我们寻找解题思路,例如,在证明三角形中位线性质定理时,就采用了图6-1的剪拼方式,将三角形转化为平行四边形使问题得以解决,请你仿照6-1的方法,在图6-2和图6-3中,分别只剪拼一次,实现下列转化:
(1) 将平行四边形转化为矩形;(2)将梯形转化为三角形
要求:选择其中一个图形,用尺规作出剪切线,保留痕迹,不写作法、其他画图,工具不限.
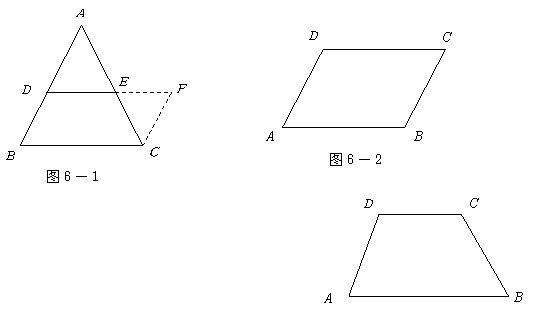 |
23.(本题满分7分)
如图7,一块四边形土地,其中![]() m,
m,

![]() m,求这块土地的面积
m,求这块土地的面积
24.种植草莓大户张华现有22吨草莓等售,有两种销售渠道,一是运往省城直接批发给零售商,二是在本地市场零售,经过调查分析,这两种销售渠道每天销量及每吨所获纯利润见下表:
| 销售渠道 | 每日销量 (吨) | 每吨所获纯 利润(元) |
| 省城批发 | 4 | 1200 |
| 本地零售 | 1 | 2000 |
受客观因素影响,张华每天只能采用一种销售渠道,草莓必须在10日内售出.
(1)若一部分草莓运往省城批发给零售商,其余在本地市场零售,请写出销售22吨草莓所获纯利润![]() (元)与运往省城直接批发零售商的草莓量
(元)与运往省城直接批发零售商的草莓量![]() (吨)之间的函数关系式;
(吨)之间的函数关系式;
(2) 怎样安排这22吨草莓的销售渠道,才使张华所获纯利润最大?并求出最大纯利润.
25.(本题满分11分)
如图8,已知:![]() 是
是![]() 的直径,
的直径,![]() 分别是
分别是![]() 的切线,切点分别为
的切线,切点分别为![]() 是
是![]() 和
和![]() 的延长线的交点.
的延长线的交点.
(1)
猜想![]() 与
与![]() 的位置关系,并加以证明;
的位置关系,并加以证明;
(2)
设![]() 的积为
的积为![]() ,
,![]() 的半径为
的半径为![]() ,试探究
,试探究![]() 与
与![]() 的关系;
的关系;
 (3)当
(3)当![]() 时,求
时,求![]() 和
和![]() 的值.
的值.
26.(本题满分13分)
已知:![]() 是
是![]() 的半径,以
的半径,以![]() 为直径的
为直径的![]() 与
与![]() 的弦
的弦![]() 相交于点
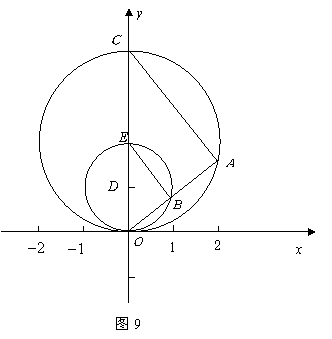
相交于点![]() ,在如图9所示的直角坐标系中,
,在如图9所示的直角坐标系中,![]() 交
交![]() 轴于点
轴于点![]() ,连结
,连结![]() .
.
(1)
当点![]() 在第一象限
在第一象限![]() 上移动时,写出你认为正确的结论:
上移动时,写出你认为正确的结论:
(至少写出四种不同类型的结论);
(2)
若线段![]() 的长是关于
的长是关于![]() 的方程
的方程![]() 的两根,且
的两根,且![]()
![]() ,求以
,求以![]() 点为顶点且经过点
点为顶点且经过点![]() 的抛物线的解析式;
的抛物线的解析式;
 (3)该抛物线上是否存在点
(3)该抛物线上是否存在点![]() ,使得
,使得![]() 是以
是以![]() 为直角边的直角三角形?若存在,求出点
为直角边的直角三角形?若存在,求出点![]() 的坐标;若不存在,说明其理由.
的坐标;若不存在,说明其理由.
2005年襄樊市初中升学统一考试
数学试题参考答案及评分标准
一、选择题(共12个小题,每小题3分,共计36分)
| 题 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答 案 | B | C | D | B | C | A | A | D | C | C | C | A |
二、填空题(共6个小题,每小题3分,共计18分)
13.![]() 14.
14.![]() 15.30
15.30
16.2或![]() (填对1个只给1分) 17.
(填对1个只给1分) 17.![]() 18.
18.![]()
二、解答题(共计66分)
19.解:原式![]() ················································ 1分
················································ 1分
![]() ·············································································· 2分
·············································································· 2分
![]() ································································ 4分
································································ 4分
当![]() 时,
时,
原式![]() ············································································ 5分
············································································ 5分
![]() ······························································································· 6分
······························································································· 6分
20.解:(1)从上到下从左到右依次填写:0.22,20,26,0.26···························· 3分
(前两空每空1分,后两空每空0.5分)
(2)优秀率为:![]() ·················································· 4分
·················································· 4分
![]() ······················································································ 5分
······················································································ 5分
答:优秀率为42%,该县(市)考试成绩为优秀的大约有![]() 人··················· 6分
人··················· 6分
21.解:设![]() ,则原方程可变形为
,则原方程可变形为![]() .········································ 1分
.········································ 1分
方程两边同乘以![]() ,约去分母,得
,约去分母,得![]() .·································· 2分
.·································· 2分
解这个方程,得![]() .·································································· 3分
.·································································· 3分
当![]() 时,
时,![]() ,去分母并解之,得
,去分母并解之,得![]() ······························· 4分
······························· 4分
当![]() 时,
时,![]() ,去分母并解之,得
,去分母并解之,得![]() ························ 5分
························ 5分
经检验,它们都是原方程的根.
原方程的根是![]() ,
,![]() ,
,![]() .·························· 6分
.·························· 6分
22.解:
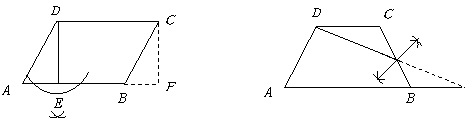 |
评分说明:每个图形中,画出剪切线给1分,画出所拼图形3分,其中一个用尺规画出剪切线的再给1分,共7分.
23.解:延长![]() 交于点
交于点![]() ··········································································· 1分
··········································································· 1分
![]()
![]() ······································································· 2分
······································································· 2分
在Rt![]() .······························································ 3分
.······························································ 3分
![]() ····················································· 4分
····················································· 4分
在Rt![]() .
.
![]() ························································ 5分
························································ 5分
![]()
![]()
![]() ·································································································· 6分
·································································································· 6分
答:这块土地的面积为![]() m2·································································· 7分
m2·································································· 7分
评分说明:若过![]() 作
作![]() 交
交![]() 于
于![]() ,过
,过![]() 作
作![]() 于
于![]() ,这样分割,
,这样分割,
参照以上评分标准分步给分.
24.解:(1)所求函数关系式为
![]() ·············································································· 2分
·············································································· 2分
即![]() ···················································································· 3分
···················································································· 3分
(2)由于草莓必须在10天内售完
则有![]() ······················································································ 5分
······················································································ 5分
解之,得![]() ····························································································· 7分
····························································································· 7分
在函数![]() 中,
中,![]()
![]() 随
随![]() 的增大而减小····················································································· 8分
的增大而减小····················································································· 8分
![]() 当
当![]() 时,
时,![]() 有最大值31200(元)························································ 9分
有最大值31200(元)························································ 9分
![]() ,
,![]() ,
,![]()
 答:用4天时间运往省城批发,6天时间在本地零售.(回答销量也可)才使获利
答:用4天时间运往省城批发,6天时间在本地零售.(回答销量也可)才使获利
润最大,最大利润为31200元.················ 10分
25.解:(1)猜想:![]() ······················· 1分
······················· 1分
证明:连结![]()
![]() 分别切
分别切![]() 于
于![]() 两点
两点
![]()
![]() ······································· 2分
······································· 2分
![]()
又![]()
![]()
![]() ·································································································· 3分
·································································································· 3分
(2)连结![]() .··························································································· 4分
.··························································································· 4分
在![]() 和
和![]() 中,
中,
![]() 是直径,
是直径,![]()
又![]() ············································ 5分
············································ 5分
![]() ··················· 6分
··················· 6分
(3)在![]() ,
,![]()
![]() ,
,![]() .
.
![]() ,
,![]() ··········································································· 7分
··········································································· 7分
![]() ,
,![]() .
.![]() ··············································· 8分
··············································· 8分
又![]() ,
,![]()
 ····························································································· 9分
····························································································· 9分
解之,得![]() .即
.即![]() 的值分别为
的值分别为![]() .
.
······················································································································ 11分
26.(1)![]()
![]() ;
;
![]()
![]() 的度数
的度数![]() 的度数.
的度数.![]()
评分说明:以上八类结论,写出一类中的一个结论给1分,同类中多写的结论不再
给分,最高不超过4分.
 (2)
(2)![]() 的长是关于
的长是关于![]() 的方程
的方程![]() 的两根.
的两根.
![]()
又![]() 是
是![]() 直径,且
直径,且![]() ,
,
![]() .
.
![]() .
.
即![]() .···················· 5分
.···················· 5分
![]() ,解之,得
,解之,得![]() .
.
![]() .······································································ 6分
.······································································ 6分
将![]() 代入原方程,得
代入原方程,得![]()
解之,得![]() ,
,
![]() ··································································· 7分
··································································· 7分
过![]() 作
作![]() 轴于
轴于![]() ,则
,则![]() .
.
![]() .即
.即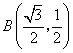 .·········································· 8分
.·········································· 8分
![]() 抛物线顶点为
抛物线顶点为![]()
![]() 设抛物线的解析式为
设抛物线的解析式为![]() .
.
将![]() 点坐标代入,得
点坐标代入,得![]() .所求抛物线解析式为
.所求抛物线解析式为![]() .················ 9分
.················ 9分
(3)抛物线上存在点![]() ,使得
,使得![]() 是以
是以![]() 为直角边的直角三角形.
为直角边的直角三角形.
①当![]() 时,点
时,点![]() 必须在
必须在![]() 的延长线上,设直线
的延长线上,设直线![]() 的解析式为
的解析式为
![]() .
.
则![]() .
.![]() .
.![]() .························································ 10分
.························································ 10分
解方程组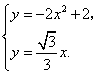 得
得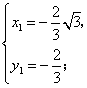
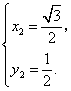 (即为
(即为![]() 点,舍去)
点,舍去)
······················································································································ 11分
②当![]() 为直角时,延长
为直角时,延长![]() 交
交![]() 于
于![]() ,连结
,连结![]() ,则
,则![]() 为
为![]() 直径,
直径,
四边形![]() 为
为![]() 内接矩形.
内接矩形.![]() .
.![]() .
.
过![]() 作
作![]() 轴于
轴于![]() ,则
,则![]() .
.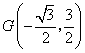 .
.
可求得直线![]() 的解析式为
的解析式为![]() ····················································· 12分
····················································· 12分
解方程组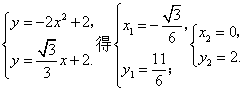 (即为
(即为![]() 点,舍去)
点,舍去)
![]() 点
点![]() 的坐标为
的坐标为![]() 或
或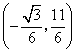 ··············································· 13分
··············································· 13分