2006年5月哈尔滨市中考数学模拟训练题
一、选择题：本大题共10个小题，每小题3分，共30分. 在每小题给出的四个选项中，只有一个选项符合题意要求.
1.下运算正确的是（ ）
A. （－a）2=－a2 B.(b3)2 ＝b5 C. 2x5＋x5＝3x5 D. y8n÷y4n＝y2n
2. 已知小明同学身高1.5米，经太阳光照射，在地面的影长为2米，若此时测得一塔在同一地面的影长为60米，则塔高应为 ( )
A. 90米 B. 80米 C. 45米 D. 40米
3. 如果关于x的不等式 (a+1) x>a+1的解集为x<1，那么a的取值范围是 ( )
A. a>0 B. a<0 C. a>-1 D. a<-1
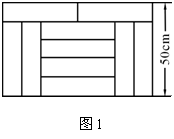
4. 如图1，宽为50 cm的矩形图案由10个全等的小长方形拼成，其中一个小长方形的面积为 ( )
A. 400 cm2 B. 500 cm2 C. 600 cm2 D. 4000 cm2
5.下列结论中，错误的命题有（ ）
①半圆是弓形；②平分弦的直径垂直平分弦；③正n边形的对称轴共有n条；④各角相等的圆的外切n边形一定是正n边形
A.0 B.1 C.2 D.4
6. 点M(－sin60°，cos60°)关于x轴对称的点的坐标是 ( )
A．(
) B．(－
) C．(－
,
) D．(－
,-)
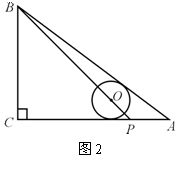
7. 如图2，在ΔABC中，∠C=90°，AC=8，AB=10，点P在AC上，AP=2，若⊙O的圆心在线段BP上，且⊙O与AB、AC都相切，则⊙O的半径是 ( )
A. 1 B. 
C.
D. 
8. 如图3，已知BC为等腰三角形纸片ABC的底边，AD⊥BC，AD=BC. 将此三角形纸片沿AD剪开，得到两个三角形，若把这两个三角形拼成一个平面四边形，则能拼出互不全等的四边形的个数是 ( )
A. 1 B.
2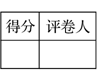 
C. 3 D. 4
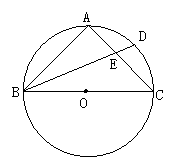
9.BC为圆的半径，O为圆心，D是AC的中点，四边形ABCD的对角线AC，BD交于点E，则下列结论：①AD=CD;②OD//AB;③AE·BD=AB·CD;④AD2=DE·BD;⑤BD·BD+CE·CA=BC2,则正确的个数是（ ）
A．2 B．3 C．4 D．5
10．两个完全相同的长方体的长、宽、高分别为5cm、4cm、3cm，把它们叠放在一起组成一个新的长方体，在这些新长方体中，表面积最大是( ).
A.
B.
C.
D.
二、填空题：本大题共10个小题,每小题3分,共30分.把答案直接填在题中横线上.
11. 分解因式：a3-a= ;
12.
十届人大三次会议温总理在班府报告中指出，中央财政将安排万元解决下岗工人再就业问题，这个数字用科学记数发表示成
;
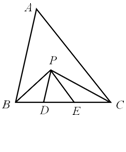
13. 如图，在ΔABC中，BC=5 cm，BP、CP分别是∠ABC和∠ACB的角平分线，且PD∥AB，PE∥AC，则ΔPDE的周长是___________ cm.
14. 若非零实数a,b满足4a2+b2=4ab，则
=___________.
15. 我市某县城为鼓励居民节约用水，对自来水用户按分段计费方式收取水费：若每月用水不超过7立方米，则按每立方米1元收费；若每月用水超过7立方米，则超过部分按每立方米2元收费. 如果某居民户今年5月缴纳了17元水费，那么这户居民今年5月的用水量为________立方米 .
16.在直角坐标系中，直线y=2006-x与函数
的图象交于点AB。设点A的标点为（x1，y1），那么长为x1，宽为y1的矩形的周长是 ;
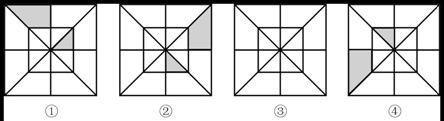
17. 分析①,②,④中阴影部分的分布规律，按此规律在③中画出其中的阴影部分.
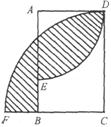
18.如图，矩形ABCD中，AB=6，BC=4，以A为圆心，AD为半径画弧交AB于点E，以C为圆心，CD为半径画弧交CB的延长线于点F，图中阴影面积是 ;
19．如图，一个正三角形经过变换依次成为正六边形、正十二边形、正二十四边形、….
当这些正多边形的周长都相等时，正六边形的面积 正十二边形的面积(填不等的
符号).
20．如图在平面直角坐标系中，·O1与x轴正半轴交于A、B两点，BO的延 长线交·O1C交y轴的负半轴于P。PC=BC=10。O1点的纵坐标为－3，D为·O1上一点，当S△ABD=4时，侧D的坐标为 .
三. 解答题：
（21题4分，22题5分，23题4分，24题5分，25题5分，26—28题各6分，30题10分，共60分）。
21．先化简
，再求值x=tan45°－cos30°.
22．换元法解方程：
。
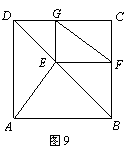23．如图9，
是正方形
的对角线
上一点，
，
，垂足分别是
.求证：
.
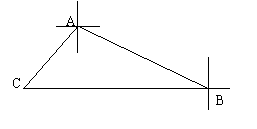
24、某中学团委到位于A市南偏东600方向50海里的B基地慰问驻车，然后乘船前往位于B基地正西方向的C哨所看望值班战士，C哨所位于A市的南偏西430方向，求C到A的距离（精确到1海里，以下数据供选用sin430≈0.68,cos430≈0.73）
25、我市部分学生参加了2004年全国初中数学竞赛决赛，并取得优异成绩. 已知竞赛成绩分数都是整数，试题满分为140分，参赛学生的成绩分数分布情况如下：
| 分数段 | 0－19 | 20－39 | 40－59 | 60－79 | 80－99 | 100－119 | 120－140 |
| 人 数 | 0 | 37 | 68 | 95 | 56 | 32 | 12 |
请根据以上信息解答下列问题：
(1) 全市共有多少人参加本次数学竞赛决赛？最低分和最高分在什么分数范围？
(2) 经竞赛组委会评定，竞赛成绩在60分以上 (含60分)的考生均可获得不同等级的奖励，求我市参加本次竞赛决赛考生的获奖比例；
(3) 决赛成绩分数的中位数落在哪个分数段内？
(4) 上表还提供了其他信息，例如：“没获奖的人数为105人”等等. 请你再写出两条此表提供的信息.
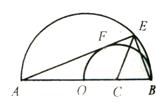26、如图AB是半圆O的直径，OB是半圆C的直径，半圆O的弦AE切半圆C于F。已知AE=8cm，求：（1）半圆C的半径；（2）△BCE的面积。
27、现计划把甲种货物1240吨和乙种货物880吨用一列货车运往某地，已知这列货车挂有A、B两种不同规格的车厢共40节，如果每节A型车厢最多可以装甲种货物35吨和乙种货物15吨，每节B型车厢最多可装甲种货物25吨和乙种货物35吨，装货时按此要求安排A、B两节车厢的节数，那么共有几种安排车厢的方案？
28、如图甲、乙两人在A、B两地间行程的函数图像如下，回答问题。
（1）甲在什么时间改变速度？
（2）甲乙在何时相距最远？（要求说明理由）
（5）甲出发后多长时间两车相距10km？
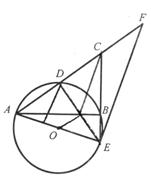
29、已知在Rt△ABC中∠ABC＝90°，D为AC上一点，且AD和CD的长是关于X的一元二次方程x2－12x＋m2＋4m＋40＝0的两个实数根，⊙O经过A、D、B三点，CB的延长线交⊙O于点E，过点E作⊙O的切线交AC延长线于点F，连续DE交AB于N，连接ON和CN。
（1）求证：△ABD为等腰三角形;
（2）过D作DM⊥AE于M，若满足CF·DE＝AE·DM，求sin∠FAB的值;
（3）在（2）条件下，求作以NO、NC为根的一元二方程。
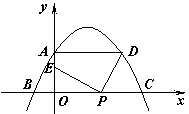
30．如图，二次函数
（
）的图象与
轴交于点A，与
轴交于点B、C，过A点作轴的平行线交抛物线于另一点D，线段OC上有一动点P，连结DP，作PE⊥DP，交y轴于点E．
（1）当
变化时，线段AD的长是否变化？若变化，请说明理由；若不变，请求出AD的长；
（2）若为定值，设
，OE=，试求关于的函数关系式；
（3）若在线段OC上存在不同的两点P1、P2使相应的点
、
都与点A重合，试求a的取值范围．