黄浦区初中毕业生学业考试数学模拟试卷
（时间：100分钟 满分：150分）2006年4月20日上午
| 题号 | 一 | 二 | 三 | 四 | 总分 |
| 得分 |
一、填空题：(本题共12小题，每小题3分，满分36分）
1、－1的相反数的倒数是 ；
2、
____________；
3、不等式
的解集是______________；
4、在实数范围内因式分解：
_____________________；
5、若
，则 x =
；
6、函数
的自变量x的取值范围是____________________；
7、若等边三角形的边长为a，则它的面积为____________.；
8、如果直线
在
轴上的截距为－2，那么这条直线一定不经过
第 象限；
9、已知＝＝＝，b＋d＋f＝50，那么a＋c＋e＝ ；
10、正多边形的中心角是36
，则这个正多边形的边数是
；
11、两圆内切，圆心距为3，一个圆的半径为5，另一个圆的半径为 ；
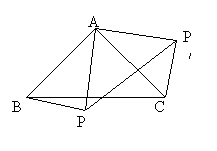
12、△ABC是等腰直角三角形，BC是斜边，将△ABP绕点A逆时针旋转
后，能与△ACP′重合。如果AP=3，那么PP′的长等于 。
二、单项选择题：（本题共4小题，每小题4分，满分16分）
【每题列出的四个答案中，只有一个是正确的，把正确答案的代号填入括号内】
13、在Rt△ABC中，∠C=90°，∠A的对边为a，已知∠A和边a，求边c，则下列关系中正确的是( )
(A) c=asinA ( B) c= (C) c=acosA (D) c=
14、在平面直角坐标中，点P（1，-3）关于x轴的对称点坐标是：
（A）（1，-3） （B）（-1，3） （C）（-1，-3） （D）（1，3）
15、一批运动服按原价八五折出售，每套a元，则它的原价为：
（A）0.85a元 （B）
元 （C）0.15a元 （D）
元
16、如图，AD∥BC,∠D=90°,DC=7,AD=2,BC=4.若在边DC上有点P使△PAD和△PBC相似，则这样的点P存在的个数有 （ ）
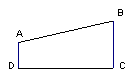(A) 1 ( B) 2 (C)
3 (D) 4
三、简答题：（本题共5小题，第19、20题，每小题9分，第21、22、23题，每小题10分，满分48分）
17、计算： 
18、用换元法解方程：
19、某区在5000名初三学生的数学测试成绩中，随机抽取了部分学生的成绩，经过整理后分成六组，绘制出的频率分布直方图（如图，图中还缺少90~100小组的小长方形），已知从左到右的第一至第五组的频率依次为0.05、0.1、0.3、0.25、0.2，第六小组的频数为25。
根据所给信息，完成下列问题：
（1）第六小组的频率是 ，并在频率分布直方图中补画它的小长方形；
（2）一共抽取了 名学生的成绩，这些成绩的中位数落在第 小组；
（3）由此可以估计全区数学测试在80分及80分以上的人数约为 人。
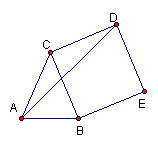
20、如图，
中，CA=CB，以BC为一边，在外作正方形BCDE，
（1） 求证：
；
（2） 若
，求
；
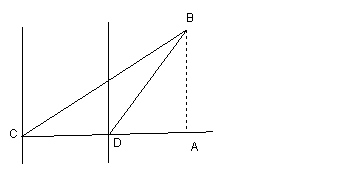21、一船从西向东航行，航行到灯塔C处，测得海岛B在北偏东60°方向，该船继续向东航行到达灯塔D处时，测得海岛B在北偏东45°方向，若灯塔C、D间的距离是10海里，海岛B周围12海里有暗礁，问该船继续航行（沿原方向）有无触礁的危险？
| |
22、如图，抛物线与直线
都经过坐标轴的正半轴上A，B两点，该抛物线的对称轴x=－1，与x轴交于点C,且∠ABC=90°求：
(1)直线AB的解析式；
(2)抛物线的解析式。
23、某商店以2400元购进某种盒装茶叶，第一个月每盒按进价增加20℅作为售价，售出50盒。第二个月每盒以低于进价5元作为售价，售完余下的茶叶。在整个买卖过程中盈利350元。求每盒茶叶的进价。
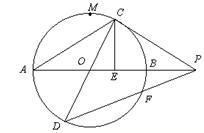
24、如图，已知AB=2，AB、CD是⊙O的两条直径，M为弧AB的中点，C在弧MB上运动，点P在AB的延长上，且PC=AC，作CE⊥AP于E，连结DP交⊙O于F。
（1）求证：当AC＝
时，PC与⊙O相切；
（2）在PC与⊙O相切的条件下，求sin∠APD的值。
 |
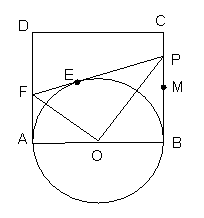
25、如图（1）正方形ABCD的边长为2，点M是BC的中点，P是线段MC上的一个动点（不运动到点M,点C），以AB为直径作⊙O，过点P作⊙O的切线交AD于点F，切点为E。
（1）求四边形CDFP的周长；
（2）设BP＝x，AF＝y，求y关于x的函数解析式，并写出自变量x的取值范围；
（3）延长DC,FP相交于点G，连接OE并延长交直线DC于H〔如图（2）〕。问是否存在点P，使⊿EFO∽⊿EHG(其中⊿EFO顶点 E、F、O与⊿EHG顶点E、H、G
为对应点）？如果存在，试求（2）中x和y的值；如果不存在，请说明理由。
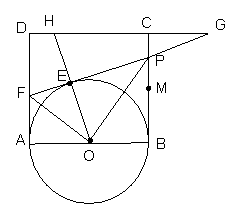
(图1) （图2）
2006年黄浦区中考模拟考数学试卷
参考答案及评分说明
2006年4月20日上午
一、填空题：（本题共12小题，每小题3分，满分36分）
⑴ 1 ⑵ x12 ⑶ x＞3 ⑷ (x－1)(x－2) ⑸ 0，8 ⑹ x＞－8
⑺
⑻ I ⑼ 30 ⑽ 10 ⑾ 2或8 ⑿ 
二、选择题：（本题共4小题，每小题4分，满分16分）
⒀ B ⒁ D ⒂ B ⒃ C
三、简答题：（本题共5小题，第19、20题，每小题9分，第21、22、23题，每小题10分，满分48分）
⒄
＝ 
（2分×4＝8分）
＝3 （1分）
⒅ 解：
设 
（1分）
得 
（1分）
化简，得 y2－y－12＝0 （1分）
(y－4)(y＋3)＝0
∴ y1＝4 y2＝－3 （1分）
当 y＝4时 x2－3x＝4， x2－3x－4＝0
(x－4)(x＋1)＝0 ∴ x1＝4 x2＝－1 （2分）
当 y＝－3时 x2－3x＝－3， x2－3x＋3＝0
∵ △＝(－3)2－4·3＜0 ∴ 无实数根 （2分）
经检验： x1＝4 x2＝－1 是否原方程的解 （1分）
⒆ ⑴ 0.1 （2分） 小长方形高度同第二组高度 （2分）
⑵ 250 （2分） 四 （2分）
⑶ 1500 （2分）
⒇ ⑴ 证明： ∵ BCDE是正方形
∴ CD＝CB （1分）
又 ∵ ⊿ABC中，CA＝CB
∴ CD＝CA （1分）
∴ ∠CAD＝∠CDA （1分）
⑵ ∵在△ABC中，CA＝CB 又 ∠ACB＝20°
（2分）
在△ACD中，∠ACD＝20°＋90°＝110° （1分）
又 AC＝CD ∴
（2分）
∴ ∠DAB＝∠CAB－∠CAD＝80°－35°＝45° （2分）
(21) 解：作BA⊥CD垂足为A （1分）
设 BA＝x海里
∵ ∠DBA＝45° ∴ DA＝BA＝x海里 （2分）
在Rt△ABC中 AB＝x海里，AC＝10＋x海里，
∠BCA＝30° ∴ 10＋x＝
（3分）
∴
（2分）
∵ 
（1分）
∴ 该船继续航行无触礁的危险 （1分）
| |
22．解：⑴ 由y＝kx－4k，得A（4，0），B（0，－4k）（k＜0）（2分）
由已知，可得在Rt△ABC中，BO⊥AC
CO＝1，OA＝4，OB＝－4k＝－4k
∴ R t△BOC∽Rt△AOB
∴ BO2＝CO·OA ∴ 16k2＝1·4 
（1分）
∴
（2分） 
∴
（1分）
⑵ 由
得 A（4，0），B（0，2）
设抛物线为 y＝a(x＋1)2＋m
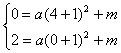得
（2分）
∴
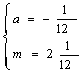（2分）
∴
即
（2分）
23．解：设每盒茶叶的进价为x元 （1分）
则
（4分）
整理，得
（2分）
去分化，化简得 x2－10x－1200＝0 （1分）
(x－40)(x＋30)＝0
∴ x1＝40 x2＝－30（舍） （2分）
经检验： x＝40 （1分）
答：每合茶叶的进价为40元 （1分）
24．⑴ 证明：在△APC中，AC＝PC，CE⊥AP于E
∵ AC＝CP＝ ， ∴ AE＝EP
（1分）
设 BP＝2a
∵ AB＝2 ∴ AO＝OB＝1 （1分）
∴ AE＝EP＝1＋a ∴ OE＝a （1分）
在 Rt△ACE中， AC2－AE2＝CE2
在 Rt△OCE中， OC2－OE2＝CE2
∴ AC2－AE2＝OC2－CE2 即 
解得
（2分）
在 △COP中，CO＝1，CP＝ OP＝2
满足 OP2＝OC2＋CP2 ∴ ∠OCP＝90°
又C在⊙O上OC为半径
∴ PC与⊙O相切于点C （1分）
⑵
在 Rt△CDP中， ∵ CD＝2，CP＝
∴ DP＝ （1分）
作DH⊥AP垂足为H （1分）
∵ ∠HOD＝∠COE ，OC＝OD，∠CEO＝∠DHO＝90°
∴ Rt△DHO≌Rt△CEO （1分）
可得
（1分）
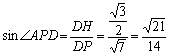
在Rt△DHP中 （2分）
25．解：⑴ ∵ 四边形ABCD是正方形
∴ ∠A＝∠B＝90°
∴ AF，BP是⊙O的切线 （1分）
又 ∵ PF是⊙O的切线
∴ FE＝FA，PE＝PB （1分）
∴ 四边形CDFP的周长为AD＋DC＋CB＝6 （1分）
⑵ 连接OE，∵ PF是⊙O的切线
∴ OE⊥PF （1分）
在Rt△AOF和Rt△EOF中 ∵ AO＝EO，OF＝OF
∴Rt△AOF≌Rt△EOF ∴ ∠AOF＝∠EOF （1分）
同理 ∠BOP＝∠EOP
∴ ∠EOF＋∠EOP＝ （1分）
∵ PF是⊙O的切线 ∴ OE⊥PF
∴ Rt△EOF∽Rt△EPO
∴ OE2＝EP·EF 即 OE2＝PB·AF （1分）
即 12＝x·y ∴
（1分）
自变量x的取值范围是 1＜x＜2 （1分）
⑶ 方法一： 存在
∵ ∠EOF＝∠AOF
∴ ∠EHG＝∠EOA＝2∠EOF （1分）
当 ∠EFO＝∠EHG＝2∠EOF时，即 ∠EOF＝30°时 （2分）
Rt△EFO∽Rt△EHG
此时在Rt△AFO中，y＝AF＝OA·tg30°＝ （1分）
（1分）
∴ 当
时 △EFO∽△EHG
方法二： 存在
∵ PF是⊙O的切线 ∴∠ HEG＝90° （1分）
又∵ ∠GCP＝90° ∠CGP＝∠EGH
∴ △EHG∽△CPG （1分）
假设存在 △EFO∽△EHG
即 △EFO∽△CPG ∴
（1分）
∵ CP∥DF ∴ △GCP∽△GDF
∴
得
 |
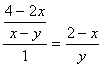∴ （1分）
 |
∵ 2－x≠0 ∴
又
得 x＝ ，
时 （1分）
使 Rt△EFO∽Rt△CPG 即 △EFO∽△EHG