二次函数05
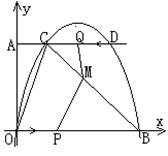
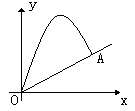1、今有网球从斜坡O点处抛出，网球的抛物线是
的图象的一段，斜坡的截线OA在一次函数
的图象的一段，建立如图所示的直角坐标系。求：（1）网球抛出的最高点的坐标。（2）网球在斜坡的落点A的垂直高度。（广东）
2、已知二次函数ｙ＝ａｘ２－４ａ图像的顶点坐标为（０，４）矩形ＡＢＣＤ在抛物线与ｘ轴围成的图形内，顶点Ｂ、Ｃ在ｘ轴上，顶点Ａ、Ｄ在抛物线上，且Ａ在Ｄ点的右侧，
（１）求二次函数的解析式
（２）设点Ａ的坐标为（ｘｙ）试求矩形ＡＢＣＤ的周长Ｌ与自变量ｘ的函数关系
（３）周长为１０的矩形ＡＢＣＤ是否存在？若存在，请求出顶点Ａ的坐标；若不存在，请说明理由。（兰州）
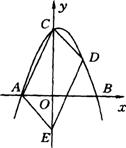
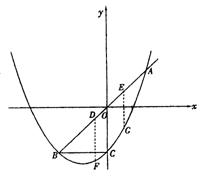
3、如图，抛物线y=-
x2+ x+6，与x轴交于A、B两点，与y轴相交于C点．
(1)求△ABC的面积；
(2)已知E点(O，-3)，在第一象限的抛物线上取点D，连结DE，使DE被x轴平分，试判定四边形ACDE的形状，并证明你的结论．（湖南岳阳）
4、如图，△ABC中，∠BAC=90°，AB=AC=1，点D是BC上一个动点(不与B、C重合)，在AC上取E点，使∠ADE=4 5°．
(1)求证：△ABD∽△DCE；
(2)设BD=x，AE=y，求y关于x的函数关系式；
(3)当△ADE是等腰三角形时，求AE的长．（湖南岳阳）
5、“五·一’’黄金周期间，李娟同学和父母自驾车去外旅游．出发时，油箱中有油b升，行驶过程中每千米耗油k升．途中李娟同学两次观察里程表A和余油量表B，当A表显示30千米时，B表显示32升；当A表显示100千米时，B表显示2 5升．设行驶的路程为z千米，油箱中的余油量为y升．求出k、b的值，并写出y关于x的函数关系式．（湖南岳阳）
6、某洗衣机在洗涤衣服时，经历了进水、清洗、排水、脱水四个连续过程，其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系如折线图所示：
根据图象解答下列问题：
（1） 
洗衣机的进水时间是多少分钟？清洗时洗衣机中的水量是多少升？
（2） 已知洗衣机的排水速度为每分钟19升，
① 求排水时y与x之间的关系式。
② 如果排水时间为2分钟，求排水结束时洗衣机中剩下的水量。（江苏）
7、如图，Rt△ABC中，∠ACB=90°，AC=4，BA=5．P是AC上的动点(P不与A、C重合)，设PC=x，点P到AB的距离为y．
(1)求y与x的函数关系式；
(2)试讨论以P为圆心，半径长为x的圆与AB所在直线的位置关系，并指出相应的x的取值范围．（广东）
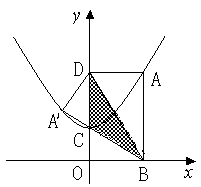
8、已知平面直角坐标系xOy中，点A在抛物线
上，过A作AB⊥x轴于点B，AD⊥y轴于点D，将矩形ABOD沿对角线BD折叠后得A的对应点为A′，重叠部分(阴影)为△BDC.
(1) 求证: △BDC是等腰三角形;
(2) 如果A点的坐标是(1，m)，求△BDC的面积;
(3) 在(2)的条件下，求直线BC的解析式，并判断点A′是否落在已知的抛物线上? 请说明理由.（广西）
9、已知二次函数
的图象经过点A（－3，－6），并与x轴交于点B（－1，0）和点C，顶点为P。
（1） 
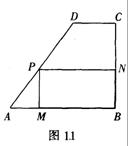求二次函数的解析式；
（2） 设点D为线段OC上一点，且∠DPC=∠BAC，求点D的坐标；
说明：若（2）你经历反复探索没有获得解题思路，请你在不改变点D的位置的情况下添加一个条件解答此题，此时（2）最高得分为3分。（辽宁）
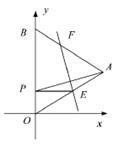10、如图，△OAB是边长为4+2
的等边三角形，其中O是坐标原点，顶点B在y轴的正半轴上.将△OAB折叠，使点A与OB边上的点P重合，折痕与OA、AB的交点分别是E、F．如果PE∥x轴,
（1）求点P、E的坐标；
（2）如果抛物线
经过点P、E，求抛物线的解析式．（山东）
11、已知：在平面直角坐标系xOy中，过点P（0，2）任作一条与抛物线y＝ax2（a＞0）交于两点的直线，设交点分别为A、B，若∠AOB＝90°，
⑴ 判断A、B两点纵坐标的乘积是否为一个确定的值，并说明理由；
⑵ 确定抛物线y＝ax2（a＞0）的解析式；
⑶当△AOB的面积为
时，求直线AB的解析式.（北京）
12、已知抛物线y＝ax2＋(b－1)x＋2.
⑴若抛物线经过点（1,4）、（－1,－2）, 求此抛物线的解析式;
⑵ 若此抛物线与直线y＝x有两个不同的交点P、Q,且点P、Q关于原点对称.
①求b的值;
② 请在横线上填上一个符合条件的a的值： a ＝＿＿,并在此条件下画出该函数的图象.（福建）
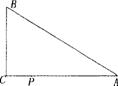
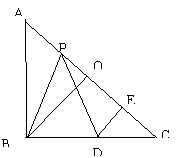
13、如图，在等要直角三角形ABC中，O是斜边AC的中点，P是斜边AC上的一个动点，D为BC上的一点，且PB＝PD，DE⊥AC,垂足为点E.
⑴ 求证：PE＝BO;
⑵ 设AC＝2a，AP＝x，四边形PBDE的面积为y，求y与x之间的函数关系式，并写出自变量的取值范围．（广东）
14、如图1I，某学校校园内有一块形状为直角梯形的空地A BCD，
其中AB//DC，∠B=90°，AB=100m，BC＝80m，CD＝40m， 现计划
在上面建设一个面积为s的矩形综合楼PMBN，其中点P在线段AD上，且
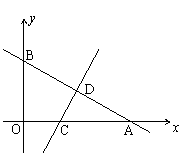PM的长至少为36m.
（1）求边AD的长；
(2）设PA = x（m），求S关于二的函数关系式，并指出自
变量x的取值范围；
(3）若S＝3300m2,求PA的长．（精确到0.lm）（广东）
15、如图，一次函数
的图象与x轴和y轴分别交于点A（6，0）和B（0，
），线段AB的垂直平分线交x轴于点C，交AB于点D.
（1）试确定这个一次函数关系式；
（2）求过A、B、C三点的抛物线的函数关系式.（江苏）
16、如图，已知矩形ABCD的边长AB=2，BC=3，点P是AD边上的一动点（P异于A、D），Q是BC边上的任意一点. 连AQ、DQ，过P作PE∥DQ交AQ于E，作PF∥AQ交DQ于F.
（1）求证：△APE∽△ADQ；
（2）设AP的长为x，试求△PEF的面积S△PEF关于x的函数关系式，并求当P在何处时，S△PEF取得最大值？最大值为多少？
（3）当Q在何处时，△ADQ的周长最小？（须给出确定Q在何处的过程或方法，不必给出证明）（江苏）
17、如图，已知抛物线
与直线y=x交于A、B两点，与y轴交于点C，OA＝OB，BC∥x轴．
(1)求抛物线的解析式。
(2)设D、E是线段AB上异于A、B的两个动点(点E在点D的上方)，DE＝
，过D、E两点分别作y轴的平行线，交抛物线于F、G，若设D点的横坐标为x，四边形DEGF的面积为y，求x与y之间的关系式，写出自变量x的取值范围，并回答x为何值时，y有最大值．（江苏）
18、已知抛物线
与y轴的交于C点，C点关于抛物线对称轴的对称点为C′。
（1）求抛物线的对称轴及C、C′的坐标（可用含m的代数式表示）；
（2）如果点Q在抛物线的对称轴上，点P在抛物线上，以点C、C′、P、Q为顶点的四边形是平行四边形，求Q点和P的坐标（可用含m的代数式表示）；
（3）在（2）的条件下，求出平行四边形的周长。（福建）
19、已知抛物线
与
轴的交点为A、B（B在A的右边），与
轴的交点为C.
(1)写出
时与抛物线有关的三个正确结论;
(2)当点B在原点的右边,点C在原点的下方时,是否存在△BOC为等腰三角形的情形?若存在,求出
的值；若不存在,请说明理由；
（3）请你提出一个对任意的值都能成立的正确命题（说明：根据提出问题的水平层次，得分有差异）.（江西）
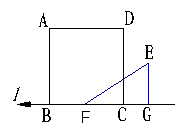
20、如图，正方形ABCD的边长为5cm，Rt△EFG中，∠G＝90°，FG＝4cm，EG＝3cm，且点B、F、C、G在直线
上，△EFG由F、C重合的位置开始，以1cm/秒的速度沿直线按箭头所表示的方向作匀速直线运动．
（1）当△EFG运动时，求点E分别运动到CD上和AB上的时间；
（2）设x（秒）后，△EFG与正方形ABCD重合部分的面积为y（cm
），求y与x的函数关系式；
（3）在下面的直角坐标系中，画出0≤x≤2时（2）中函数的大致图象；如果以O为圆心的圆与该图象交于点P（x，
），与x轴交于点A、B（A在B的左侧），求∠PAB的度数．（四川）
21、在以O为原点的平面直角坐标系中，抛物线
与y轴交于点C（0，3），与x轴正半轴交于A、B两点（B在A点的右侧），抛物线的对称轴是x=2，且
。
（1） 求此抛物线的解析式；
（2） 设此抛物线的顶点为D，求四边形ADBC的面积。（湖北）
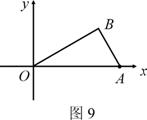
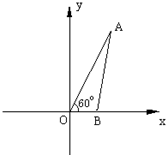
22、如图9，已知O为坐标原点，∠AOB=30°，∠ABO=90°，且点A的坐标为(2,0).
(1) 求点B的坐标；
(2) 若二次函数y=ax2+bx+c的图象经过A、B、O三点，求此二次函数的解析式；
(3) 在(2)中的二次函数图象的OB段(不包括点O、B)上，是否存在一点C，使得四边形ABCO的面积最大？若存在，求出这个最大值及此时点C的坐标；若不存在，请说明理由.（四川）
23、如图,在平面直角坐标系中,∠AOB=60°,点B坐标为（2，0），线段OA的长为6． 将△AOB绕点O逆时针旋转60°后,点A落在点C处,点B落在点D处．
⑴请在图中画出△COD;
⑵求点A旋转过程中所经过的路程（精确到0.1）；
⑶求直线BC的解析式（江苏）
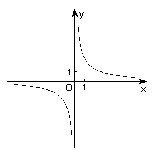
24、有一个
，
，
，
，将它放在直角坐标系中，使斜边
在轴上，直角顶点
在反比例函数
的图象上，求点
的坐标．（常州）
25、教室里放有一台饮水机（如图），饮水机上有两个放水管．课间同学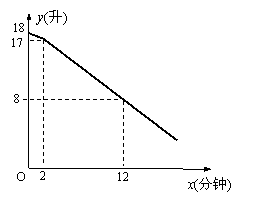
们依次到饮水机前用茶杯接水．假设接水过程中水不发生泼洒，每个同学所接的水量都是相等的．两个放水管同时打开时，他们的流量相同.放水时先打开一个水管，过一会儿，再打开第二个水管，放水过程中阀门一直开着．饮水机的存水量y（升）与放水时间x（分钟）的函数关系如图所示：
（1）求出饮水机的存水量y（升）与放水时间x（分钟）(x≥2)的函数关系式；（4分）
（2）如果打开第一个水管后，2分钟时恰好有4个同学接水结束，则前22个同学接水结束共需要几分钟？（4分）
（3）按（2）的放法，求出在课间10分钟内班级中最多有多少个同学能及时接完水？（4分）（江苏）
26、如图，边长为1的正方形OABC的顶点O为坐标原点，点A在x轴的正半轴上，点C在y轴的正半轴上．动点D在线段BC上移动(不与B，C重合)，连接OD，过点D作DE⊥OD，交边AB于点E，连接OE．记CD的长为t．
(1) 当t＝
时，求直线DE的函数表达式；
(2) 如果记梯形COEB的面积为S，那么是否存在S的最大值？若存在，请求出这个最大值及此时t的值；若不存在，请说明理由；
(3) 当OD2＋DE 2的算术平方根取最小值时，
求点E的坐标．（浙江）
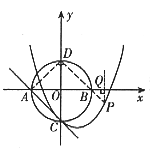
27、如图所示，在平面直角坐标系xOy中，半径为1的圆O分别交x轴、y轴于A、B、C、D四点，抛物线
经过点C且与直线AC只有一个公共点。
（1）求直线AC的解析式；
（2）求抛物线的解析式；
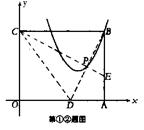（3）点P为（2）中抛物线上的点，由点P作x轴的垂线，垂足为点Q，问：此抛物线上是否存在这样的点P，使
？若存在，求出P点坐标；若不存在，请说明理由。（山西）
28、一张矩形纸片OABC平放在平面直角坐标系内，O为原点，点A在x的正半轴上，点C在y轴的正半轴上，OA＝5，OC＝4。
① 如图，将纸片沿CE对折，点B落在x轴上的点D处，求点D的坐标；
② 在①中，设BD与CE的交点为P，若点P，B在抛物线
上，求b，c的值；
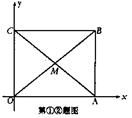③ 若将纸片沿直线l对折，点B落在坐标轴上的点F处，l与BF的交点为Q，若点Q在②的抛物线上，求l 的解析式。（浙江）
29、一张矩形纸片OABC平放在平面直角坐标系内，O为原点，点A在x的正半轴上，点C在y轴的正半轴上，OA＝5，OC＝4。
①求直线AC的解析式；
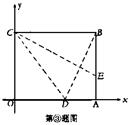②若M为AC与BO的交点，点M在抛物线
上，求k的值；
③将纸片沿CE对折，点B落在x轴上的点D处，试判断点D是否在②的抛物线上，并说明理由。（浙江）
30、已知：抛物线的解析式为
（1） 求证：此抛物线与x轴必有两个不同的交点；
（2） 若此抛物线与直线
的一个交点在y轴上，求m的值。
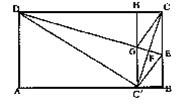31、已知，在矩形ABCD中，AB＝2，E为BC上一点，沿直线DE将矩形折叠，使C点落在AB边上的C¹点处，过作C¹H⊥DC，C¹H分别交DE、DC于点G、H，连结CG，C C¹，C C¹交GE于点F。
（1） 求证：四边形CG C¹E为菱形；
（2） 
设
，并设
，试将y表示成x的函数
（3） 当（2）中所求得的函数的图象达到最高点时，求BC的长。（江苏）
32、如图，已知直角坐标系内的梯形AOBC（O为原点），AC∥OB，OC⊥BC，AC，OB的长是关于x的方程x2－(k+2)x+5=0的两个根，且S△AOC：S△BOC=1：5。
（1）填空：0C=________，k=________；
（2）求经过O，C，B三点的抛物线的另一个交点为D，动点P，Q分别从O，D同时出发，都以每秒1个单位的速度运动，其中点P沿OB由O→B运动，点Q沿DC由D→C运动，过点Q作QM⊥CD交BC于点M，连结PM，设动点运动时间为t秒，请你探索：当t为何值时，△PMB是直角三角形。
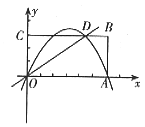33、矩形OABC在直角坐标系中的位置如图所示，A、C两点的坐标分别为A6，0）、C（0，3），直线
与BC边相交于点D。
（1）求点D的坐标；
（2）若抛物线
经过D、A两点，试确定此抛物线的表达式；
（3）P为x轴上方（2）中抛物线上一点，求△POA面积的最大值；
（4）设（2）中抛物线的对称轴与直线OD交于点M，点Q为对称轴上一动点，以Q、O、M为顶点的三角形与△OCD相似，求符合条件的Q点的坐标。
34、已知：在平面直角坐标系xOy中，一次函数
的图象与x轴交于点A，抛物线
经过O、A两点。
（1）试用含a的代数式表示b；
（2）设抛物线的顶点为D，以D为圆心，DA为半径的圆被x轴分为劣弧和优弧两部分。若将劣弧沿x轴翻折，翻折后的劣弧落在⊙D内，它所在的圆恰与OD相切，求⊙D半径的长及抛物线的解析式；
（3）设点B是满足（2）中条件的优弧上的一个动点，抛物线在x轴上方的部分上是否存在这样的点P，使得
？若存在，求出点P的坐标；若不存在，请说明理由。