2006年初三数学中考模拟测试题（A.）
（考试时间：120分钟 巻面总分150分）
第一部分 选择题（共36分）
一、选择题（下列各题所给答案中，只有一个答案是正确的，每小题3分，共36分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
1．若
，则a的取值范围为( )
(A)a≥2 (B)a≤2 (C)a≥―2 (D)a≤―2
2. .下列计算，正确的是（ ）
A.
B.
C.
D.
)=
3. 图1中几何体的主视图是
 |  |  | |||||||
 | |||||||||
 | |||||||||
4. 抛物线
的对称轴是（）
Ａ、直线x=－１ Ｂ、直线 x=1 Ｃ、直线x=－2 Ｄ、直线x=2
5. “神舟六号”宇航员费俊龙、聂海胜在太空共看到了76次日出日落，日行程约676000公里，用科学记数法表示日行程为( )
A．6.76×107 公里 B．6.76×105公里 C．0.676×106公里 D．67.6×106公里
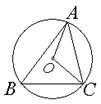6. 如图2，⊙O是△ABC的外接圆，连接OA、OC，
⊙O的半径R=2，
，则
弦AC的长为 （ ）
A. 3
B. 
|
D.
7. 两个不相等的实数m，n满足
，
，则mn的值为
(A) 6 (B) －6
(C) 4 (D) －4
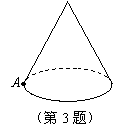
8. 如图3，圆锥的母线长是3，底面半径是1，A是底面圆周上一点，从点
A出发绕侧面一周，再回到点A的最短的路线长是
(A)
(B)
(C)
(D)3
9. 某青年排球队12名队员的年龄情况如下：
| 年龄（单位：岁） | 18 | 19 | 20 | 21 | 22 |
| 人 数 | 1 | 4 | 3 | 2 | 2 |
则这个队队员年龄的众数和中位数是（ ）
A、19，20 B、19，19 C、19，20.5 D、20，19
10.一个密闭不透明的盒子里有若干个白球，在不允许将球倒出来的情况下，为估计白球的个数，小刚向其中放入8个黑球，摇匀后从中随机摸出一个球记下颜色，再把它放回盒中，不断重复，共摸球400次，其中88次摸到黑球，估计盒中大约有白球（ ）
A、28个 B、30个 C、36个 D、42个
11. 下列四个函数：
① 
② 
③ 
④ 
其中，函数y的值随着x值得增大而减少的是
A、 ① ， B、② ， C、③ ， D、④ ；
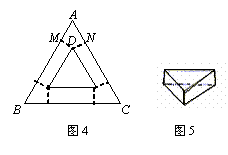
12. 用一块等边三角形的硬纸片（如图4）做一个底面为等边三角形且高相等的无盖的盒子（边缝忽略不计，如图5），在△ABC的每个顶点处各剪掉一个四边形，其中四边形AMDN中，∠MDN的度数为（ ）
A. 100° B. 110°
C. 120° D. 130°
第二部分 非选择题（共114分）
二、填空题：（每题3分，共24分）
13. 请写出一个你喜欢的：当x<0时，函数值随自变量的增大而增大的函数关式：
________________________________________。
14．如图6，在甲、乙两地之间修一条笔直的公路，
从甲地测得公路的走向是北偏东48°。甲、乙两地间
|
同时开工，若干天后，公路准确接通，则乙地所修公
路的走向是南偏西 度。
15.如图7，矩形纸片ABCD中，AD=9cm，AB=3cm，
将纸片沿虚线EF折叠，使得点D与点B重合，
那么折痕EF的长度为 cm..
 |
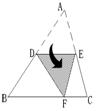16. 如图8，D、E为△ABC两边AB、AC的中点，将△ABC沿线D折叠，使点A落在点F处，若∠B=55°，则∠BDF=_______0.
|
17. 若x1、x2是方程x2+3 x+2=0的两个根，那么x12+x22的值等于 _________.
18. ．用长为4 cm、5 cm、6 cm的三条线段围成三角形的事件是__________.
19. 在日常生活中如取款、上网等都需要密码．有一种用“因式分解” 法产生的密码，方便记忆．原理是：如对于多项式
，因式分解的结果是
，若取x=9，y=9时，则各个因式的值是：(x－y)=0，(x+y)=18，(x2+y2)=162，于是就可以把“018162”作为一个六位数的密码．对于多项式
，取x=10，y=10时，用上述方法产生的密码是： (写出一个即可)．
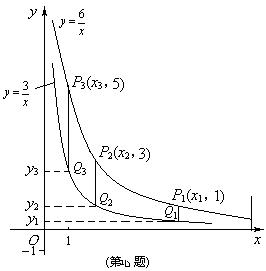
20.两个反比例函数
，
在第一象限内的图象如图所示, 点P1，P2，P3，…，P2 005在反比例函数图象上，它们的横坐标分别是x1，x2，x3，…，x2
005，纵坐标分别是1，3，5，…，共2
005个连续奇数，过点P1， P2，P3，…，P2 005分别作y轴的平行线，与的图象交点依次是Q1（x1，y1），Q2（x2，y2），Q3（x3，y3），…，Q2 005（x2 005，y2 005），则y2 005= ．
三、解答题：（21、22、23每题8分，24、25、26、27每题10分，28题12分，29题14分）
21．计算：
+
22．已知实数a满足a2＋2a－8=0，求
的值.
23．为节约用电，某学校于本学期初制定了详细的用电计划。如果实际每天比计划多用2度电，那么本学期的用电量将会超过2530度；如果实际每天比计划节约2度电，那么本学期用电量将会不超过2200度电。若本学期的在校时间按110天计算，那么学校每天用电量应控制在什么范围内？
24．为了调查淮安市今年有多少名考生参加中考，小华从全市所有家庭中随机抽查了200个家庭，发现其中10个家庭有子女参加中考．
⑴本次抽查的200个家庭中，有子女参加中考的家庭的频率是多少？
⑵如果你随机调查一个家庭，估计该家庭有子女参加中考的概率是多少？
⑶已知淮安市约有1.3×106个家庭，假设有子女参加中考的每个家庭中只有一名考生，请你估计今年全市有多少名考生参加中考?
25．如图10将RT△ABC沿斜边AB向右平移5cm，得到RT△DEF。已知AB=10 cm，BC=8 cm。
求图中阴影部分三角形的周长。
|
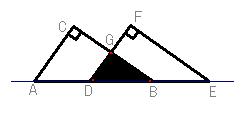
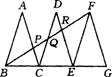
26．如图11，△ABC、△DCE、△FEG是三个全等的等腰三角形，底边BC、CE、EG在同一直线上，且AB=
，BC=1，连结BF，分别交AC、DC、DE于点P、Q、R，（1）求证：△BFG∽△FEG，并求出BF的长；（2）观察图形，请你提出一个与点P相关的问题，并解答（根据提出问题的层次和解答过程进行评分）。
|
27．某电信部门新开设甲、乙两种通讯方式，它们的通话费
（元）与通话时间
（分钟）之间的函数关系图象分别如下图：
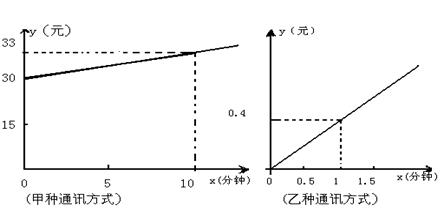
请你根据图象解答下列的问题：
（1） 写出甲、乙两种通讯方式的通话费（元）与通话时间（分钟）之间的函数关系式；（4分）
（2） 若某人一个月内预计使用话费180元，则他应选择哪种通讯方式较合算？并说明理由。（6分）
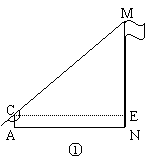
28在一次实践活动中，某课题学习小组用测倾器、皮尺测量旗杆的高度，他们设计了如下方案（如图①所示）：
(1)在测点A处安置测倾器，测得旗杆顶部M的仰角∠MCE=α;
(2)量出测点A到旗杆底部N的水平距离AN=
;
(3)量出测倾器的高度AC=
.
根据上述测量数据，即可求出旗杆的高度MN.
如果测量工具不变，请仿照上述过程，设计一个测量某小山高度（如图②）的方案：
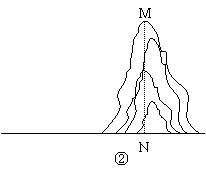
(1)在图②中，画出你测量小山高度MN的示意图（标上适当字母）；
(2)写出你设计的方案.
29．已知抛物线
（1）证明抛物线顶点一定在直线y=-x+3上；
（2）若抛物线与x轴交于M、N两点，当OM·ON=3，且OM≠ON时，求抛物线的解析式；
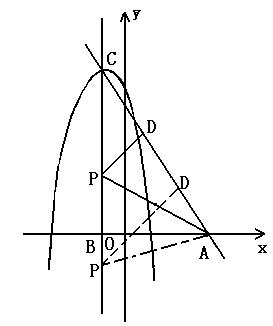
（3）若（2）中所求抛物线顶点为C，与y轴交点在原点上方，抛物线的对称轴与x轴交于点B，直线y=-x+3与x轴交于点A。点P为抛物线对称轴上一动点，过点P作PD⊥AC，垂足D在线段AC上。试问：是否存在点P，使
？若存在，求出点P的坐标；若不存在，请说明理由。
答案：
一、CDDBBADCAACC
二、13. 答案不唯一，比如
等
14. 48
15.
16. 70
17. 5
18. 必然事件
19. 101030，或103010，或301010
20. 2004.5
21．解：原式=3
+3-2-
（4分）
=3 （8分）
22．=
··························· 3分
(每正确分解一个因式给1分)
=
··································································································· 4分
由a2＋2a－8=0知，(a＋1)2=9，······························································· 6分
∴ =
，即的值为.································· 8分
23．解：设学校每天用电量为x度，依题意可得：
解得：
，即学校每天用电量应控制在21度～22度范围内。
24．⑴
=
………………………………………………………………………………3分
⑵……………………………………………………………………………………………6分
⑶1.3×106×=6.5×104…………………………9分
答：略………………………………………………10分
25．解:在RT△ABC中,AC=
………………………….2分
∵D为AB的中点,B为DE的中点,DF∥AC,BC∥EF,
∴GC=GB,GD=GF………………………………………………………5分
∴DG=
,BG=
……………………….8分
∴DG+BG+DB=3+4+5=12…………………………………………..10分
26．（1）证明：∵△ABC≌△DCE≌△FEG
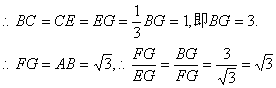
又∠BGF=∠FGE，∴△BFG∽△FEG.…………3分
∵△FEG是等腰三角形，∴△BFG是等腰三角形，∴BF=BG=3.………………4分
（2）A层问题（较浅显的，仅用到了1个知识点）.
例如：①求证：∠PCB=∠REC.（或问∠PCB与REC是否相等？）等；
②求证：PC//RE.（或问线段PC与RE是否平行？）等.
B层问题（有一定思考的，用到了2~3个知识点）.
例如：①求证：∠BPC=∠BFG等，求证：BP=PR等；②求证：△ABP∽△CQP等，
求证：△BPC∽△BRE等；③求证；△ABP∽△DQR 等；④求BP：PF的值等.
C层问题（有深刻思考的，用到了4个或4个以上知识点、或用到了（1）中结论）.
例如：①求证：△ABP∽△BPC∽ERF；②求证：PQ=RQ等；
③求证：△BPC是等腰三角形；④求证：△PCQ≌△RDQ等；⑤求AP：PC的值等；⑥求BP的长；⑦求证：PC=
（或求PC的长）等.
A层解答举列.求证：PC//RE.
证明：∵△ABC≌△DCE，∴∠PCB=∠REB，∴PC//RE.
B层解答举例.求证：BP=PR.
证明：∵∠ACB=∠REC，∴AC//DE. 又∵BC=CE，∴BP=PR.
C层解答举例.求AP：PC的值.
解：
评分说明：①考生按A层、B层、C层中某一层次提出问题均给1分，若继续给出正确的解答则分别再加1分、2分、3分；②若考生提出其它问题，并作正确解答，可参照各相应层次的评分标准评分；③在本题中，若考生提出的是与点P无关的问题，却是正确的结论及解答，就不再考虑其层次，只给1分.
27．解：（1）从图象中可知：
甲种通讯方式：
2分
乙种通讯方式：
4分
（2）当
时，解得：=500（分钟）；…6分
当
=180时，解得：=450（分钟）； …8分
所以选择甲种通讯方式较合算。………9分
28．（1）正确画出示意图. ……………………………………………………2分
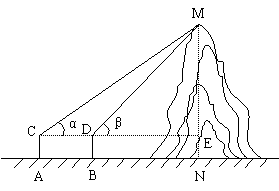
（2）①在测点A处安置测倾器，测得此时M的仰角
；
②在测点A与小山之间的B出安置测倾器（A、B与N在同一条直线上），测得此时山顶M的仰角
；
③量出测倾器的高度AC＝BD＝h，以及测点A、B之间的距离AB＝m.根据上述测量数据，即可求出小山的高度MN. …………………………………………………6分
 |
29．（1）
∴顶点坐标为（m,-m+3）
∴顶点在直线y=-x+3上………………………………3分
（2）∵抛物线与x轴交于M、N两点
∴△>0
即：
解得：m<3……………………………………5分
∵OM·ON=3
∴
当
时，
，
∴m=0，m=-1
∴当m=0时，
（与OM≠ON矛盾，舍）
∴m=-1
当
时，
，
∴m=2，m=-3
∴
……………………………………8分
（3）∵抛物线与y轴交点在原点的上方
∴
，
∴C（-1，4），B（-1，0）
∵直线y=-x+3与x轴交于点A
∴A（3，0）
∵BA=BC
∴∠PCD=45°
∴设PD=DC=x，
则
，
∵
∴
解得：
当
时，
∴
∴
∴
当
时，
∴
∴
∴或
………………………………14分