初三数学中考模拟题二

（2）初三数学中考模拟题二

班次 ＿＿＿＿　　 姓名 ＿＿＿＿＿　　  计分 　　　　　 

填空题：

1、方程2x²+7x=4的根为 　　　　　　　　 。

2、关于x的方程x²+kx+6=0有一个根是-2，那么k＝　　 。另一根为　　　　。

3、函数y＝在　　　　  时有意义。

4、3Cos²60°－Sm45°•tan30°+tan60°＝　　　　　　 。

5、等腰三角形腰长为3，底边为2，则底角的余弦值为　　　　　  。

6．的因式分解的结果是____________________．

7．圆锥可以看成是直角三角形以它的一条直角边所在的直线为轴，其余各边旋转一周而成的

　 面所围成的几何体，那么圆台可以看成是___________________________所在的直线为轴，

　 其余各边旋转一周而成的面所围成的几何体；如果将一个半圆以它的直径所在的直线为轴旋

　 转一周，所得的几何体应该是___________．

 

8．若1<x<4,则化简的结果是　　　　　  。

9．已知点P在第二象限，且到x轴的距离是2，到y轴的距离是3，则点P的坐标为　　　 。

10．若关于x的方程的一个根是－2，则它的另一个根是　　　　  。

11．已知，则分式的值为　　　　  。

12．已知⊙O中，两弦AB与CD相交于点E，若E为AB的中点，CE:ED=1:4,AB=4,则CD的长等于

　　 　　　　　　。

13．若正三角形、正方形、正六边形的周长都相等，它们的面积分别记为,则

　  由大到小的排列顺序是　　　　　 。

二、选择题（每小题3分，共30分）

1、当锐角A＞30°时，cosA的值是　　　。

　 A: 小于　　 B:大于　　　C:　小于 　　 D: 大于

2、关于x的方程x²+ax+a²＝0的两根和是3a－8，则两根之积是　　　　 。

　 A：－4　　　 B：4　　　 C：2　　  D：9

3、下列函数中，y是x的反比例函数的为　　　　　 。

　 A：y＝－3x　　　B：y＝2x+1　　 C：y＝　　　 D：y＝－

4、如果二次三项式x²-ax+4是一个完全平方式，那么a的值是　　　　  。

　 A:　2　　　 B: 4　　 C:　±2　　  D:　±4

5．下列各式中计算正确的是（　　）．

 （A）　　　　　 　　　　　　　  （B）

 （C）　　　　　　　 （D）

6．1米长的标杆直立在水平的地面上，它在阳光下的影长为0.8米；此时，若某电视塔的影长为100米，

　 则此电视塔的高度应是（　　）．

 （A）80米　　　　　（B）85米　　　　　　（C）120米　　　　　（D）125米

7．已知2是关于x的方程的一个解，则的值是（　  ）．

 （A）3　　　　　　　 （B）4　　　　　　　　 （C）5　　　　　　　　 （D）6

8．下列函数关系中，可以看作二次函数模型的是（　  ）．

（A）在一定的距离内汽车的行驶速度与行驶时间的关系

（B）我国人口年自然增长率为1％，这样我国人口总数随年份的变化关系

（C）竖直向上发射的信号弹，从发射到落回地面，信号弹的高度与时间的关系（不计空气阻力）

（D）圆的周长与圆的半径之间的关系

9．如图，∠AOP=∠BOP=15°，PC∥OA，PD⊥OA，若PC=4，则PD等于（　  ）．

 （A）4　　　　（B）3　　　　　（C）2　　　　　（D）1

10.在某次数学测验中，随机抽取了10份试卷，其成绩如下：

85，81，89，81，72，82，77，81，79，83

　 则这组数据的众数、平均数与中位数分别为

 （A）81,82,81　(B)81,81,76.5　(C)83,81,77　 (D)81,81,81

11.制造一种产品，原来每件的成本是100元，由于连续两次降低成本，现在的成本是81元，

　 则平均每次降低成本

 （A）8.5%　 (B) 9%　(C) 9.5% (D) 10%

12.已知AB、CD是⊙O的两条直径，则四边形ACBD一定是

　(A)等腰梯形　(B)菱形　 (C) 矩形　 （D）正方形

13．相交两圆的公共弦长为16cm，若两圆的半径长分别为10cm和17cm，则这两圆的圆心距为

 （A）7cm  (B)16cm　 (C)21cm　(D)27cm

三、计算与作图：

1.　　　　 计算：1－＋5()^－1＋(－2002)⁰－；

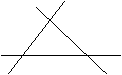
2.　　　　 某市有一块由三条马路围成的三角形绿地（如图），现准备在其中建一小亭供人们小憩，使小亭中心到三条马路的距离相等，试确定小亭的中心位置（不写作法，保留作图痕迹）。　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　  　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

四、解答题 （解答应写出文字说明，证明过程或推演步骤．）

1．（本小题满分7分）当时，求代数式的值．

2、已知关于x的方程k²x²+(2k-1)x+1=0的两个不等实数根为x₁、 x₂（7分）

　  1）求k的取值范围

　 

　  2）是否存在一个实数k，使方程的两个实数根互为相反数？如果存在，求出k值；

　　如果不存在，说明为什么？

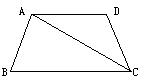
3、  知：如图，在梯形ABCD中，AD∥BC，AB=CD，∠D=120°，对角线CA平分∠BCD，且梯形的周长为２０，求AC的长及梯形面积S。

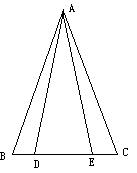
4、  如图，点D、E在△ABC的边BC上，BD=CE,AB=AC.求证：AD=AE

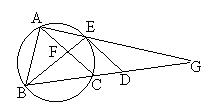
5、如图，已知D是BC延长线上一点，DE切△ABC的外接圆于E，DE∥AC，AE、BC的延长线交于G，BE交AC于F，求证：（1）BF平分∠ABC；（2）AE²=AB·CD；

 

6、 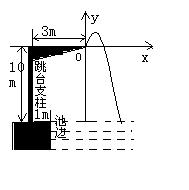 跳水运动员进行10米跳台跳水训练时，身体（看成一点）在空中的运动路线是如图所示坐标系下经过原点O的一条抛物线（图中标出的数据为已知条件）。要跳某个规定动作时，正常情况下，该运动员在空中的最高处距水面米，入水处距池边的距离为4米，同时，运动员在距水面高度为5米以前，必须完成规定的翻腾动作，并调整好入水姿势，否则就会出现失误，（1）求这条抛物线的解析式；（2）在某次试跳中，测得运动员在空中运动路线是如图抛物线，且运动员在空中调整好入水姿势时，距池边的水平距离为米，问此次跳水会不会失误？并通过计算说明理由。