高一数学试卷
一、选择题(每题5分。在每小题的四个选项中,只有一个符合要求。)
1.设集合![]() 则满足上述条件的集合A的个数为 ( )
则满足上述条件的集合A的个数为 ( )
A.1 B.2 C.3 D.4
2.设函数f(x)是实数集上的奇函数,且满足![]()
则f(x)在(1,2)上是 ( )
A.增函数且f(x)<0 B.增函数且f(x)>0 C.减函数且f(x)<0 D.减函数且f(x)>0
3.已知![]() =(—2 , 5)的起点为(—1 ,—2),则它的终点为
( )
=(—2 , 5)的起点为(—1 ,—2),则它的终点为
( )
A.(—3 ,3) B.(—1 ,7) C.(1 ,—7) D.(—2 ,5)
4. 在三角形ABC中,若sinAsinB﹤cosAcosB,则三角形ABC一定是 ( )
A 正三角形 B 直角三角形 C 锐角三角形 D 钝角三角形
5.![]() ,
,![]() 满足何条件时,等式
满足何条件时,等式![]() 成立
( )
成立
( )
A ![]() 与
与![]() 同向 B
同向 B ![]() 与
与![]() 反向 C
反向 C ![]() 与
与![]() 垂直 D
垂直 D ![]() 与
与![]() 垂直且模相等.
垂直且模相等.
6.已知点P(cos![]() ,tan
,tan![]() )在第三象限,则在区间[0,2π]内的
)在第三象限,则在区间[0,2π]内的![]() 的取值范围是 ( )
的取值范围是 ( )
A (0, ![]() )
B (
)
B (![]() , π)
, π) ![]() C (π,
C (π, ![]() ) D (
) D (![]() , 2π)
, 2π)
7、已知a=(1,2),b=(-3,2),向量ka+b与向量a-3b垂直, 向量ma+b与向量a-3b平行
(k,m为实数), k+3m的值为 ( )
(A) 17 (B)18 (C)19 (D)20
8.设函数f(x)对x![]() R都满足f(3+x)=f(3-x),且方程f(x)=0恰有6个不同的实数根,
R都满足f(3+x)=f(3-x),且方程f(x)=0恰有6个不同的实数根,
则这6个实根的和为 ( )
(A)0 (B)9 (C)12 (D)18
9、已知幂函数![]() 在第一象限单调递增,幂函数
在第一象限单调递增,幂函数![]() 在第一象限单调递减,
在第一象限单调递减,
则函数![]() ( )
( )
A、在(-![]() ,0)上单调增
B、在(-
,0)上单调增
B、在(-![]() ,0)上单调减
,0)上单调减
C、在(-![]() ,-1)上单调增
D、在(-
,-1)上单调增
D、在(-![]() ,-1)上单调减
,-1)上单调减
10、函数![]() ,使
,使![]() 成立的
成立的![]() 的值的集合为 ( )
的值的集合为 ( )
A、是![]() B、有且只有一个元素 C、有且只有二个元素 D、有无数个元素
B、有且只有一个元素 C、有且只有二个元素 D、有无数个元素
11.函数![]() 是奇函数,则
是奇函数,则![]() 等于(以下均有
等于(以下均有![]() ) ( )
) ( )
A.![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
12.已知![]() ,若记
,若记![]() ,则
,则![]() 的值为
( )
的值为
( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
二.填空题(每题4分,共4小题。16分。把答案填在横线上。)
13、已知![]() ,则
,则![]() 。
。
14.函数f(x)=log(2x-1)![]() 的定义域是
。
的定义域是
。
15.已知![]() ,
,![]() ,且
,且![]() 与
与![]() 夹角为钝角,则实数
夹角为钝角,则实数![]() 的取值范围是
的取值范围是
16.若对n个向量![]() 存在n个不为0的实数
存在n个不为0的实数![]() ,使得
,使得![]() 成立,则称向量
成立,则称向量![]() 为线形相关。则使得
为线形相关。则使得![]() 线形相关的实数
线形相关的实数![]() 依次可以取______________。
依次可以取______________。
(写出一组即可,不必考虑所有情况。)
三.解答题。
17.(12分)已知tan![]() ,tan
,tan![]() 是方程
是方程![]() 的两个实根,求
的两个实根,求![]() 的值。
的值。
18.(12分)已知![]() =(3,—4),
=(3,—4),![]() =(6,—3),
=(6,—3),![]()
①若A,B,C三点共线,求实数m满足的条件。
②当m 为何值时,三角形ABC是以A为直角顶点的直角三角形。
19.已知向量![]() .
.
求函数f(x)的最大值,最小正周期,并写出f(x)在[0,π]上的单调区间.
20 (本小题满分12分) 根据市场调查某商品在最近40天内的价格![]() 与时间
与时间![]() 的
的
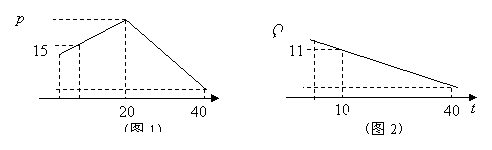 关系用图1中的一条折线表示,销售量
关系用图1中的一条折线表示,销售量![]() 与时间
与时间![]() 的关系用图2中的线段表示
的关系用图2中的线段表示![]()
(1)、分别写出图1表示的价格与时间的函数关系![]() 图2表示的销售量与时间的函数关系
图2表示的销售量与时间的函数关系![]()
(2)、求这种商品的销售额![]() (销售量与价格之积)的最大值及此时的时间。
(销售量与价格之积)的最大值及此时的时间。
21、(12分)设![]()
(1)判断f(x)的奇偶性;
(2)证明f(x)为R上的增函数;
(3)若方程f(x2 –2x-a)=0在(0,3)上恒有解,求实数a的取值范围。
22.(14分)设![]()
![]()
![]()
![]() ,
,![]() 与
与![]() 的夹角为
的夹角为![]() 与
与![]() 的夹角为
的夹角为![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
参考答案
1-12..DAADC BBDCC DB
13. 24
14.
(0,1) ![]() 15.
15. ![]() 且
且![]() 16. 2,-1,1_。
16. 2,-1,1_。
17. 解,由题意知:![]()
![]()
![]() ;
;
则原式=![]()
=![]() =
=![]()
18. 解,
![]() =(3,1)
=(3,1) ![]() =(2-m, -m+1)
=(2-m, -m+1)
![]() A,B,C三点共线
A,B,C三点共线
![]()
![]() 与
与![]() 共线
共线
![]() 3(
3(![]() )-(2-m)=0
)-(2-m)=0
![]() m=
m=![]()
20. (1)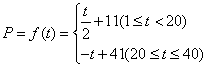 (3分
(3分![]() (6分
(6分
(2)、当![]() 时,
时,![]()
![]() 或
或![]() 时,
时,![]() (10分)
(10分)
当![]() 时,
时,![]()
在![]() 上是减函数,即当
上是减函数,即当![]() 时,
时,![]()
而![]() ,那么,当
,那么,当![]() 或
或![]() 时,
时,![]() (14分)
(14分)
21. 解,(1)(2)略。 (3)由于 ![]() ∴
∴![]()
由f(x)的单调性知
x2-2x-a=0 x∈(0,3)
∴a=x2-2x x∈(0,3)
=(x-1)2-1 x∈(0,3)
∴ a∈[-1,3)
∴实数a的取值范围为[-1,3]