《不等式的性质》培优资料
1.(江苏2007届调研题)若a<b<0,则下列不等式不能成立的是( )
A.![]() >
>![]() B.2a>2b
B.2a>2b
C.a>b D.(![]() )a>(
)a>(![]() )b
)b
2.(江苏省溧阳中学第一学期第一次阶段性测试)下列命题中,使命题![]() 是命题
是命题![]() 成立的充要条件的一组命题是 ( )
成立的充要条件的一组命题是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.(厦门市高三年质量检测理)“![]() ”是“
”是“![]() ”的 ( )
”的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
4.(东城区第一学期期末数学目标检测)若![]() 则下列结论不正确的( )
则下列结论不正确的( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5. (扬州密卷)已知a, b, c∈R, a+b+c=0,abc>0,T=++,则( )
(A)T>0 (B)T<0 (C)T=0 (D)无法判断T的正负
6.(西城区抽样测试文)设![]() ,则下列不等式成立的是 ( )
,则下列不等式成立的是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.(广州市普通高中毕业班综合测试文科卷)如果a<0, -1<b<0,那么下列不等式中正确的是 ( )
A.a<ab2<ab B.ab2<a<ab C.a<ab<ab2 D.ab2<ab<a
8.(湖北省八校第二次联考文)若a、b、c、d均为实数,使不等式![]() 和
和![]() 都成立的一组值(a,b,c,d)是
.(只要写出适合条件的一组值即可)
都成立的一组值(a,b,c,d)是
.(只要写出适合条件的一组值即可)
9.(2006年上海春)若![]() ,则下列不等式成立的是(
)
,则下列不等式成立的是(
)
(A)![]() . (B)
. (B)![]() . (C)
. (C)![]() .(D)
.(D)![]() .
.
10.(06上海)、如果![]() ,那么,下列不等式中正确的是( )
,那么,下列不等式中正确的是( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
11.(05年高考湖北卷)对任意实数a,b,c,给出下列命题:
①“![]() ”是“
”是“![]() ”充要条件; ②“
”充要条件; ②“![]() 是无理数”是“a是无理数”的充要条件③“a>b”是“a2>b2”的充分条件;④“a<5”是“a<3”的必要条件.
是无理数”是“a是无理数”的充要条件③“a>b”是“a2>b2”的充分条件;④“a<5”是“a<3”的必要条件.
其中真命题的个数是 ( )
A.1 B.2 C.3 D.4
12.(04年北京卷)如果a,b,c满足c<b<a,且ac<0,那么下列选项中不一定成立的是
(A)ab>ac (B)c(b-a)>0 (C)cb2<ab2 (D)ac(a-c)<0
13.(东城区06学年度第一学期期末教学目标检测)已知a<0,b<-1,则下列不等式成立的是( )
A.a>![]() >
>![]() B.
B.![]() >
>![]() >a
>a
C.![]() >
>![]() >a
D.
>a
D.![]() >a>
>a>![]()
14.(2006北京海淀区模拟样卷一)给出三个条件:
①xt2>yt2; ②![]() ;
③x2>y2
;
③x2>y2
其中能分别成为x>y的充分条件的是 ( )
A.①②③ B.②③ C.③ D.①
15.(2006年江苏省南京市高考数学冲刺卷)一杯浓度为![]() 的糖水,加一点糖m,其浓度会变大,即
的糖水,加一点糖m,其浓度会变大,即![]() <
<![]() ,感觉会甜一点;如果将两杯浓度不一样甜的糖水
,感觉会甜一点;如果将两杯浓度不一样甜的糖水![]() <
<![]() 倒在一起,甜度会怎样?请你写出一个不等关系说明其甜度关系_________
倒在一起,甜度会怎样?请你写出一个不等关系说明其甜度关系_________
16.(湖南师大附中高三第一次月考题)已知
![]() 则不
则不
![]() ( )
( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
![]()
![]()
17(05全国统一考试仿真试卷).已知a>b>c,a+b+c=0![]() 方程ax2+bx+c=0的两个实根为x1,x2
方程ax2+bx+c=0的两个实根为x1,x2
(1)
证明:-![]() ;
;
(2) 若x12+x1x2+x22=1,求x12-x1x2+x22
(3)
求![]()
参考答案
B,D,A,C,B,D,A,(9,3,-2,-1),C,A
B,C,C,D
15.甜度在原来两种甜度之间,即![]() <
<![]() <
<![]() ,
,
此题具有开放性问题答案也可以是![]() <
<![]() <
<![]() 或
或![]() <
<![]() <
<![]() 等
等
16.C
17.解:(1)![]() a>b>c,a+b+c=0,
a>b>c,a+b+c=0,
∴![]() ,
,
∴a>0,1>![]()
∴![]()
(2)(方法1) ![]() a+b+c=0
a+b+c=0
∴ ax2+bx+c=0有一根为1,
不妨设x1=1,则由x12+x1x2+x22=1可得x2(x2+1)=0,
而x2=x1x2=![]() <0(3c<a+b+c=0),∴ x2=-1
<0(3c<a+b+c=0),∴ x2=-1
∴x12-x1x2+x22=3
(方法2) ![]() x1+x2=-
x1+x2=-![]() ,x1x2=
,x1x2=![]()
由x12+x1x2+x22=(x1+x2)2- x1x2=![]() =1,
=1,
∴![]()
∴x12-x1x2+x22=
x12+x1x2+x22-2x1x2=1-2x1x2=1+![]()
(3)由(2)知,
![]() =
=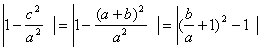
![]()
![]()
∴-![]()