高一数列单元检测卷
一.选择题(45分)
1.在等差数列{an}中, a7=9, a13=-2, 则a25=
A -22 B -24 C 60 D 64
2.若数列{an}由a1=2, an+1= an+2n (n≥1) 确定, 则a100的值是
A 9900 B 9902 C 9904 D 10100
3.数列1,(1+2),(1+2+22),…,( 1+2+22+…+2n-1+…)的前n项和是
A 2n B 2n-2 C 2n+1- n -2 D n·2n
4.数列{an}是公差不为零的等差数列, 并且a5, a8, a13是等比数列{bn}的相邻三项. 若b2=5, 则bn=
A 5·(![]() )n-1 B 5·(
)n-1 B 5·(![]() )n-1 C 3·(
)n-1 C 3·(![]() )n-1 D 3·(
)n-1 D 3·(![]() )n-1
)n-1
5.已知等差数列![]() 的公差为2,若
的公差为2,若![]() 成等比数列, 则
成等比数列, 则![]() =
=
A –4 B –6 C –8 D –10
6.设数列![]() 是等差数列,且
是等差数列,且![]() 是数列
是数列![]() 的前n项和,则
的前n项和,则
A S4<S3 B S4==S2 C S6<S3 D S6>S3
7. 已知由正数组成的等比数列{an}中,公比q=2, a1·a2·a3·…·a30=245, 则a1·a4·a7·…·a28=
A 25 B 210 C 215 D 220
8.若![]() 是等差数列,首项
是等差数列,首项![]() ,则使前n项和
,则使前n项和![]() 成立的最大自然数n是:
成立的最大自然数n是:
A.4005 B.4006 C.4007 D.4008
9.设![]() ,对于
,对于![]() ,令
,令![]() ,则乘
,则乘![]()
A.![]() B.15
B.15
C.48 D.720
10.在等比数列{an}中, a1<0, 若对正整数n都有an<an+1, 那么公比q的取值范围是
A q>1 B 0<q<1 C q<0 D q<1
11.已知数列{an}的前n项和Sn=a[2-(![]() ) n-1]- b[2-( n+1)(
) n-1]- b[2-( n+1)(![]() ) n-1]( n=1,2,…),其中a, b是非零常数.则存在数列{xn},{yn}使得
) n-1]( n=1,2,…),其中a, b是非零常数.则存在数列{xn},{yn}使得
A an= xn + yn,其中{xn}为等差数列,{yn}为等比数列
B an= xn + yn,其中{xn}和{yn}都为等比数列
C an= xn·yn其中{xn}为等差数列,{yn}为等比数列
D an= xn·yn其中{xn}和{yn}都为等比数列
12. 已知f(x)=bx+1为x的一次函数, b为不等于1的常数, 且g(n)=![]() , 设an= g(n)- g(n-1) (n∈N※), 则数列{an}是
, 设an= g(n)- g(n-1) (n∈N※), 则数列{an}是
A. 等差数列 B。等比数列 C 。递增数列 D 。 递减数列
13.将数列{3n-1}按“第n组有n个数”的规则分组如下:(1),(3,9),(27,81,243),…,则第100组中的第一个数是
A.34950 B.35000 C. 35010 D.35050
14.已知数列![]() 满足
满足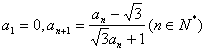 ,则
,则![]() =
=
A.0 B.![]() C.
C.![]() D.
D.![]()
15.某人为了观看2008年奥运会,从2001年起,每年5月10日到银行存入a元定期储蓄,若年利率为p且保持不变,并约定每年到期存款均自动转为新的一年定期,到2008年5月1日,将所有的存款及利息全部取回,则可取回的钱的总数(税前)为 (单位:元)
A.![]() B.
B.![]()
C.![]() D.
D.![]()
二.填空题(20分)
16.已知等差数列{an}的公差d≠0, 且a1, a3, a9成等比数列, 则![]() 的值是
.
的值是
.
17.已知数列1,![]() 成等差数列, 且1,
成等差数列, 且1,![]() 成等比数列,则
成等比数列,则![]() 的值为
的值为
.
18.设数列![]() 的前
的前![]() 项和为
项和为![]() (
(![]() ). 关于数列
). 关于数列![]() 有下列三个命题:
有下列三个命题:
(1)若![]() 既是等差数列又是等比数列,则
既是等差数列又是等比数列,则![]() ;
;
(2)若![]() ,则
,则![]() 是等差数列;
是等差数列;
(3)若![]() ,则
,则![]() 是等比数列.
是等比数列.
这些命题中,真命题的序号是 .
19.已知函数![]() ,数列
,数列![]() 的通项公式是
的通项公式是![]() (
(![]() ),当
),当 ![]() 取得最小值时,
取得最小值时,![]() .
.
20.定义“等和数列”:在一个数列中,如果每一项与它的后一项的和都为同一个常数,那么这个数列叫做等和数列,这个常数叫做该数列的公和. 已知数列![]() 是等和数列, 且a1=2,
公和为5, 那么
是等和数列, 且a1=2,
公和为5, 那么 ![]() ,且这个数列的前21项和S21的值为
.
,且这个数列的前21项和S21的值为
.
数学答卷 姓名______, 班级________, 学号_________
一、选择题(45分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
二、填空题(20分)
16_________, 17_________, 18_________, 19_________, 20______, _______.
三、解答题(每小题8分,共40分)
21.已知等差数列{an}共2n+1项, 其中奇数项之和为290, 偶数项之和为261, 求第n+1项及项数2n+1的值.
22.已知等比数列![]() 的公比为q,且
的公比为q,且![]() ,第17项的平方等于第24项,求使
,第17项的平方等于第24项,求使![]() 成立的n的取值范围。
成立的n的取值范围。
23.已知数列![]() 为等差数列,且
为等差数列,且![]()
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)证明![]()
24.已知数列{an}为等差数列, 公差为d, {bn}为等比数列, 公比为q, 且d= q=2,
b3+1= a10=5, 设cn= anbn.
(Ⅰ)求数列{cn}的通项公式;
(Ⅱ)求数列{cn}的前n项和为Sn,
25.数列{an}满足![]() =1且8
=1且8![]() -16an+1+2an+5=0 (n³1)。记
-16an+1+2an+5=0 (n³1)。记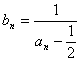 (n³1)。
(n³1)。
(1) 求b1、b2、b3的值;并证明![]() 是等比数列;
是等比数列;
(2) 求数列{anbn}的前n项和Sn
参考答案:
一、BBCDB BABCB CBABD
二、![]() 17.
17.![]() 18.①,②,③ 19. 11 20. 3, 52
18.①,②,③ 19. 11 20. 3, 52
三、
21.第n+1项为29项, 项数为19.
22.![]()
23.![]()
24.cn= anbn=(2n-15)2 n-1, Sn=(2n-17) 2 n+17.
25.![]() ,
,![]()
![]()